原标题：动态规划求解最大子段和 (两种写法+还原最优解)

前言

在这篇文章中，我将介绍动态规划求解 最大子段和(即最大子数组累加和问题) 的两种写法思路及其还原最优解，后面还包含了一点小小的优化。?

(本文作者： Amdeus，未经允许不得转载哦。)

---

最大子段和解析

最大子段和问题描述

给定一个长度为 len 的序列: a[0], a[1], a[2] ... a[len - 1] ，求在这个序列中一个子区间 [j, i] 使得 a[j] + a[j + 1] +...+ a[i] 的和最大，并求出这个最大累加和。
比如一个序列为 {-6, 7, -1, 5, 11, -7, 2}，那么其最大子段和结果为 22，所求子区间范围是 [1, 4]。

为什么可以用动态规划

最优子结构性质

最优子结构: 原问题的最优解包含了子问题的最优解。

假设求得了某两个最大子段和区间，分别为 [j, i] 和 [j, i - 1]，前一个子区间的元素分别为 {a[j], a[j + 1] ... a[i]}，后一个子区间的元素分别为 {a[j], a[j + 1] ... a[i - 1]}。我们很容易发现，后一个子区间 [j, i - 1] 同时也是前一个子区间 [j, i] 的子区间。

假设我们的两个子区间范围内的最大累加和分别是 maxA 和 maxB，那么可以得出 maxA 必然包含了 maxB。也就是说 maxA = maxB + a[i] or 0，当 a[i] 为正数时，我们可以加上 a[i]，这样 [j, i] 的最大累加和相较于 [j, i - 1] 就更大；当 a[i] 为负数时，我们加上它之后只会减小区间 [j, i] 的最大累加和，相较于 [j, i - 1] 反而更小，所以此时不加上 a[i]。

由此可见，最大子段和问题是满足最优子结构性质的。

无后效性

无后效性: 某阶段的状态一旦确定，则此后过程的演变不再受此前各状态及决策的影响。
简单地说，就是当前一个状态确定之后，之后的过程中的任何决策都不会影响当前的这个已确定的状态，只是和当前这个状态有关而已。就好像是"未来与过去无关"，我们无法改变过去，但是我们过往的事迹是和我们的一生都息息相关的。?

对于最大子段和问题，我们都是在先前的状态基础上更新当前的最优解。假设求得之前某个最大子段和区间 [j, i - 1]，那么我们现在要求区间 [j, i] 的最大累加和，那么我们只需要在之前区间 [j, i - 1] 确定状态的基础上，更新当前区间 [j, i] 的最优解，这个问题就是在上一个小标题里我说到的是否加上 a[i] 。

由此可见，最大子段和是满足无后效性的。

重叠子问题性质

重叠子问题: 在过程中重复计算相同的子问题，即子问题之间不是相互独立的，子问题的最优解在之后的决策中会被用到。
在上面的阐述中也已经提到，假设我们求得某两个最大子段和子区间分别是 [j, i] 和 [j, i - 1]，区间 [j, i - 1] 的最大累加和maxB 是先前已经确定的状态，我们求解 [j, i] 的最大累加和 maxA 需要用到这个 maxB，无需再次计算 maxB。

很显然，最大子段和问题也是满足重叠子问题性质的。

综上，我们可以用动态规划算法来求解最大子段和(最大子数组累加和)问题。

算法步骤

1、首先我们需要定义 dp[] 数组来记录每个状态下的最优解；

2、为了还原最优解，我们需要定义 rec[] 数组来记录边界下标；

3、构建递推方程，求出最大子段和，并还原具体最优解。

两种思路概述

在求解这个问题时，我想到了两种求解最大子段和问题的思路。一种是从前往后记录的方法，一种从后往前记录的方法(这些名字都是我自己取的?)。
下面我会分别介绍这两种思路，并且给出各自的递推方程。???

---

从前往后记录法

从前往后记录法解释

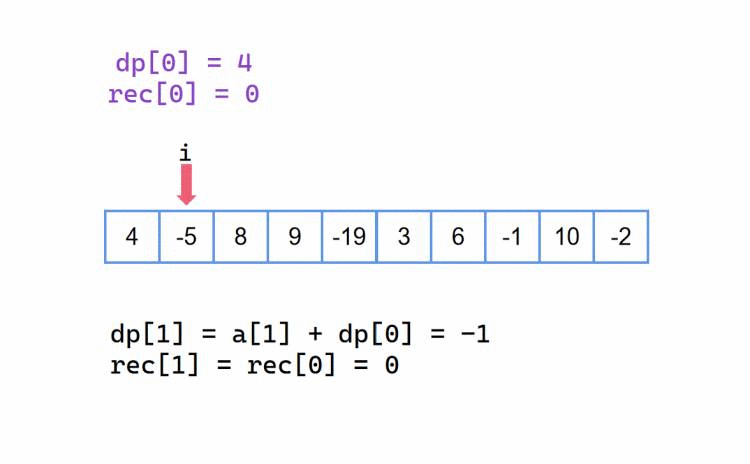
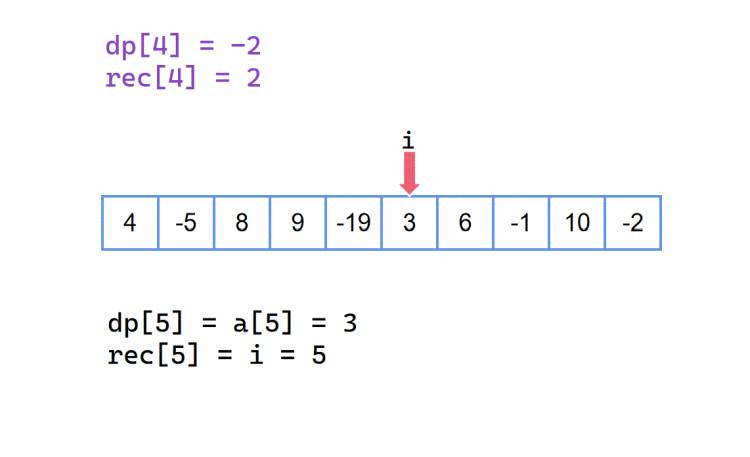
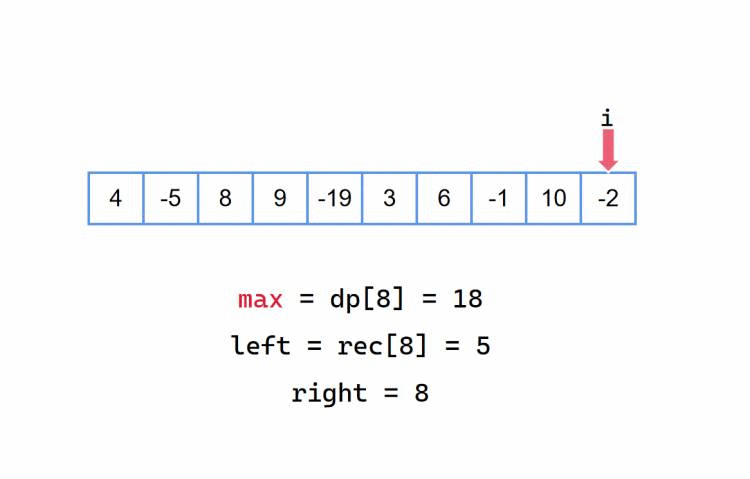
我们的 dp[] 数组，在这个从前往后记录的方法中，记录的是以下标为 i 为结尾下标的子区间的最大累加和，与此同时 rec[] 数组记录的是对应以下标为 i 为结尾下标的子区间的左边界(这些很重要?)。也就是说，如果我们的最大子段和最终答案是 dp[i]，那么对应的区间是 [rec[i],文章来源地址6554.html i]，我们也可以定义 left = rec[i], right = i，这样更清晰一点。初始情况下，dp[0] = a[0], rec[0] = 0。

对于从前往后记录的方法，我们可以得到如下的式子:

由此可以得到对应动态规划递推方程:

其实可以简单地理解成我们在当前的状态下是否抛弃前面部分的最大累加和。
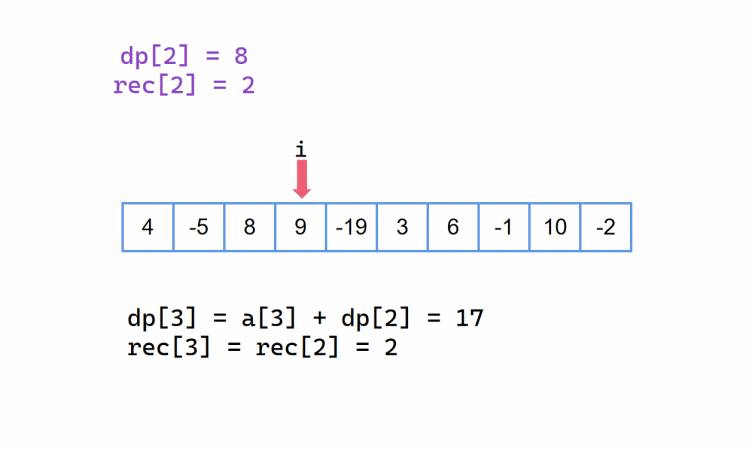
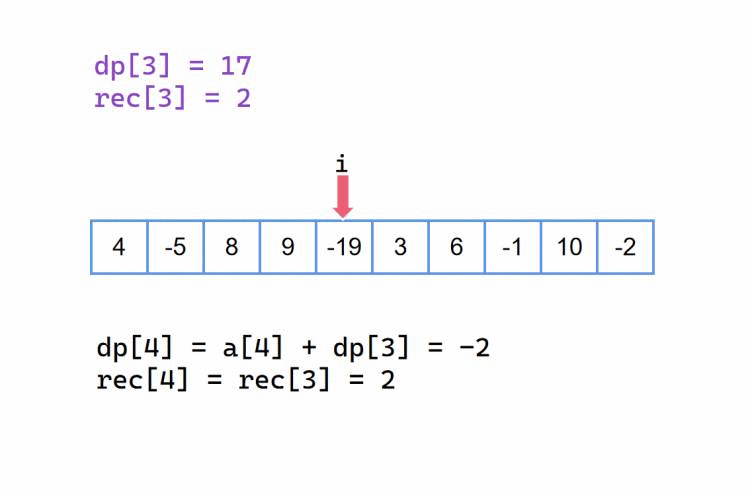
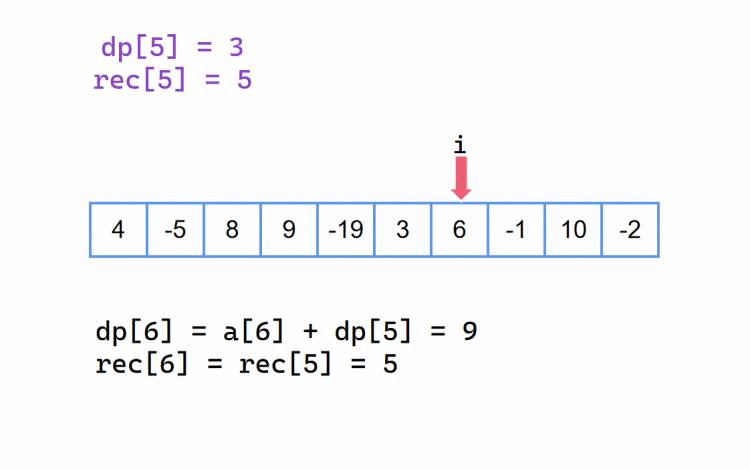
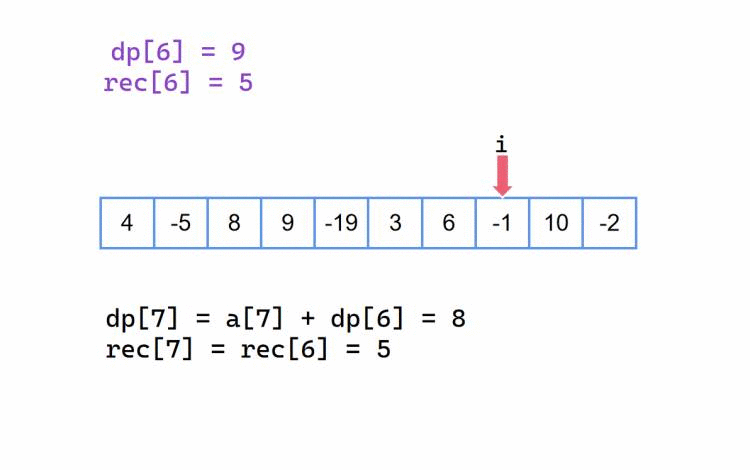
当我们前半部分最大累加和 dp[i-1] 是一个正数，那么我们当前元素 a[i] 加上它，就是当前以 i 为结尾的最大累加和，此时就是 dp[i] = a[i] + dp[i - 1]；
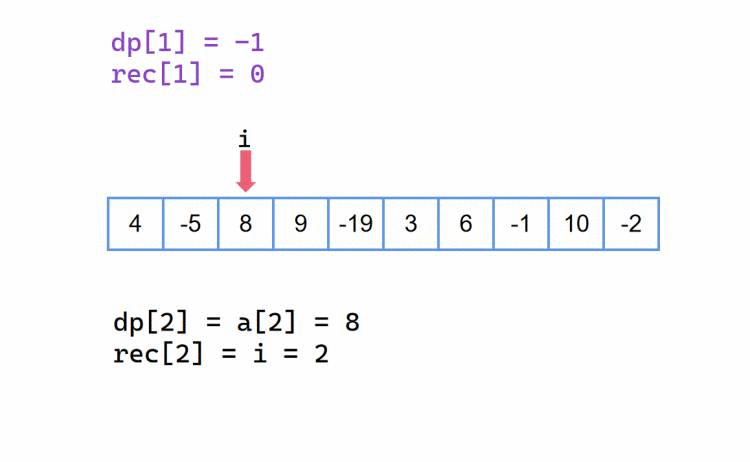
当我们前半部分最大累加和 dp[i-1] 都已经是一个负值(或者0)了，那么我们当前元素 a[i] 加上它只会让当前以 i 为结尾的最大累加和更小，所以我们要丢弃它，从新的起点下标开始，也就是此时的 dp[i] = a[i]。

同时我们写出对应的 rec[] 的方程:

rec[i] 此时就是记录的对应 dp[i] 的左边界，即区间的起始下标。
当 dp[i - 1] 是一个正数，我们会加上它，自然也会延续之前的起始下标，也就是这里的 rec[i] = rec[i - 1]；
当 dp[i - 1] 是一个非正数，我们选择丢弃前半部分，那么我们以当前下标 i 为新的起始点，也就是 rec[i] = i。

从前往后记录法动态演示

我们以 {4, -5, 8, 9, -19, 3, 6, -1, 10, -2} 为例

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

从前往后记录法实现代码

void Find_Subarray_Max1(int a[], int n){
int *dp = new int[MAX]; //用于存储以下标为 i 作为结尾的最大子数组累加和
int *rec = new int[MAX]; //用于记录下标为 i 作为结尾的最大子数组的开头下标
/* 动态规划部分 */
dp[0] = a[0];
rec[0] = 0; //从开头开始
for(int i = 1; i <= n; i++){
if(dp[i - 1] > 0){
dp[i] = a[i] + dp[i - 1];
rec[i] = rec[i - 1];
}else{
dp[i] = a[i]; //丢弃前部分和为负的子段
rec[i] = i;
}
}
/* 还原最优解部分 */
int max = INT_MIN; //足够小的负数
int left, right;
for(int i = 0; i <= n; i++){
if(max max = dp[i];
left = rec[i];
right = i;
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] dp;
delete[] rec;
/* 作者 Amdeus */
}


时间复杂度

动态规划部分进行了 n - 1次扫描，还原最优解部分进行了 n 次扫描，由此可知时间复杂度为 O(n)。

从后往前记录法

从后往前记录法解释

说实话这个思路略有一点逆思维，其实只是扫描方向的区别，就好像是把数组翻转一下，事实证明从后往前记录的顺序也是同样可以解决最大子段和问题的，只不过我在网上很少看到有人写，所以决定自己来写一下。?

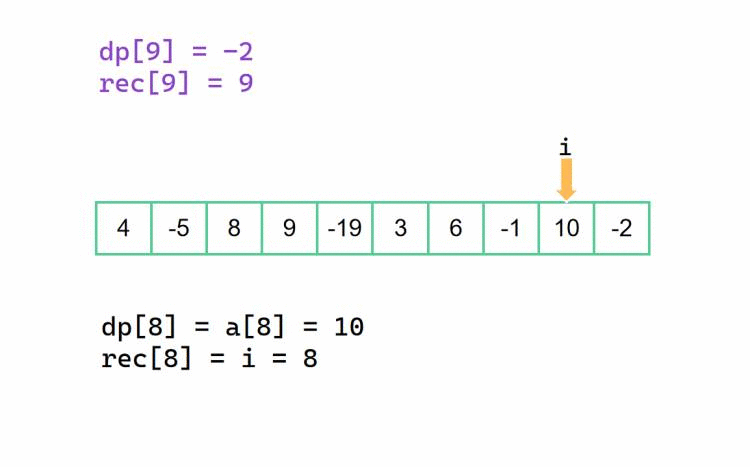
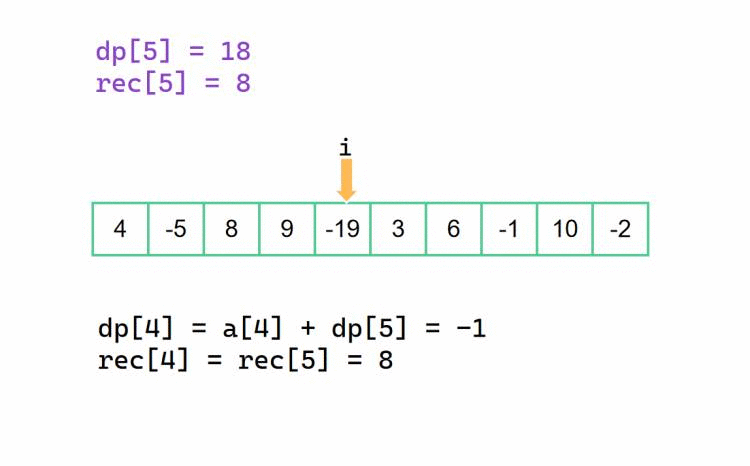
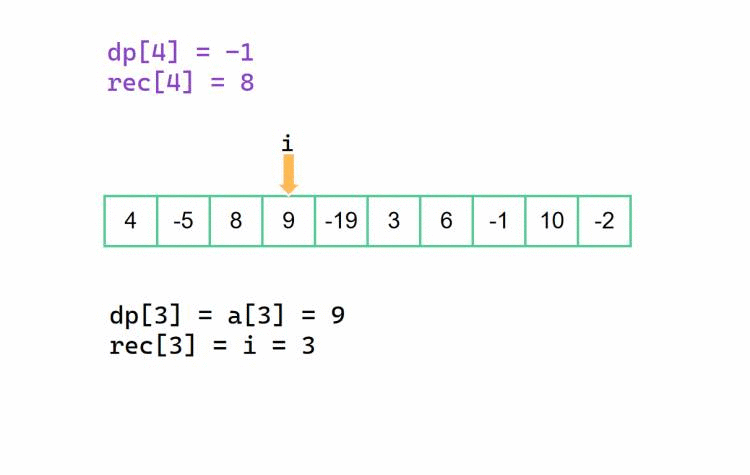
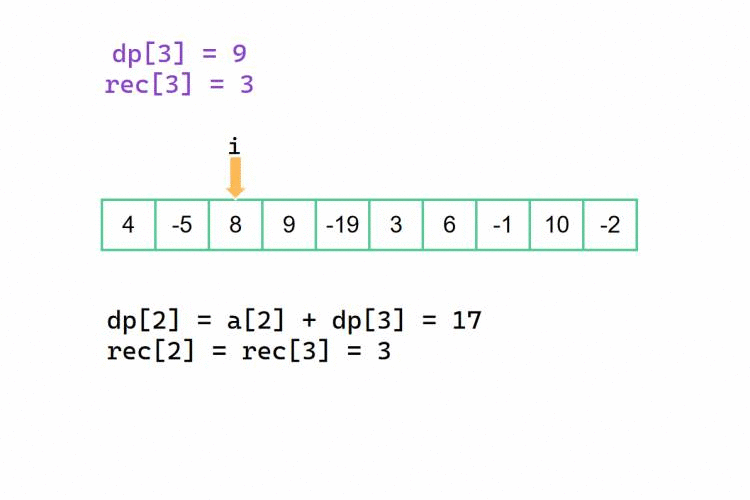
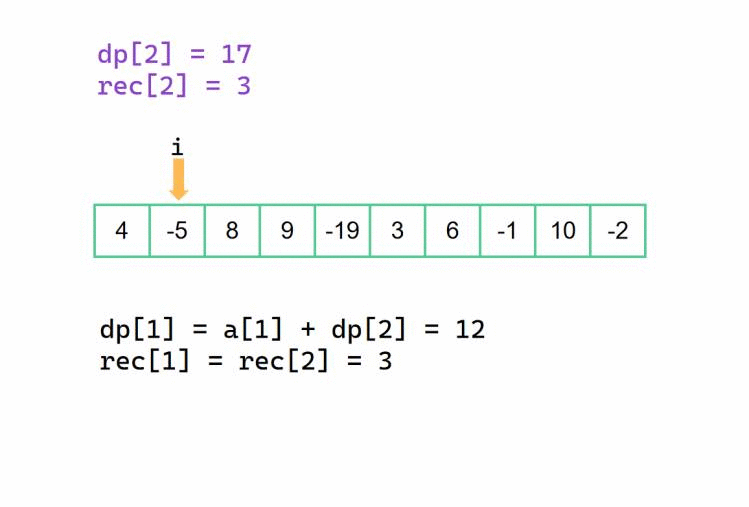
不同的是我们的 dp[] 数组，在这个从后往前记录的方法中，记录的是以下标为 i 为起始下标的子区间的最大累加和，与此同时 rec[] 数组记录的是对应以下标为 i 为起始下标的子区间的右边界(这些还是很重要?)。也就是说，如果我们的最大子段和最终答案是 dp[i]，那么对应的区间是 [i, rec[i]]，我们也可以最后定义 left = i, right = rec[i]。初始情况下，若数组最后一个下标为n，那么dp[n] = a[n], rec[n] = n。
(注意和之前方法的不同哟~)

类似地对于从后往前记录我们可以得到如下的式子:

由此得到对应的动态规划递推方程:

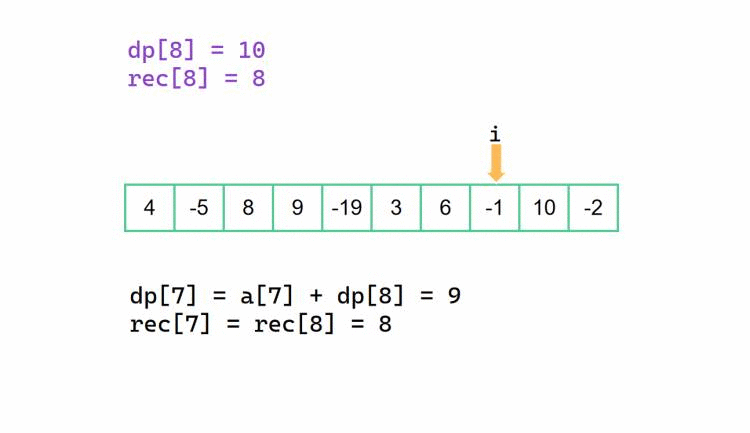
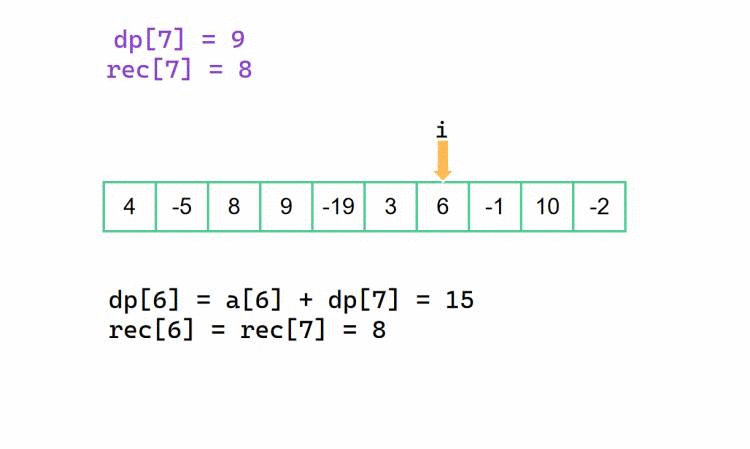
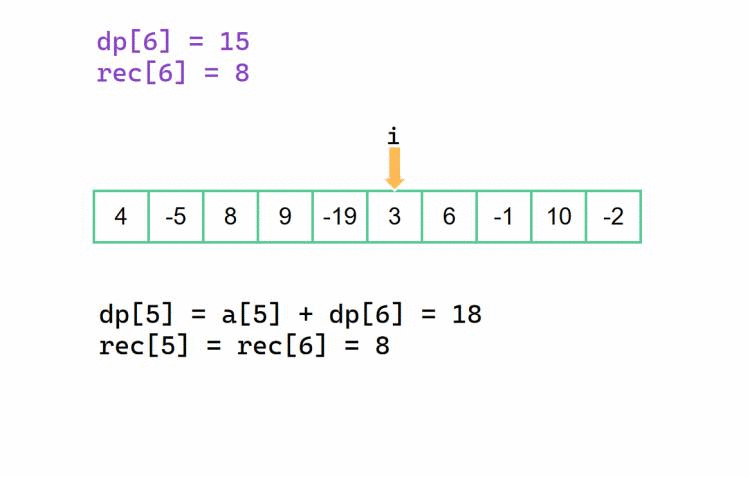
还是和前面的方法差不多的，不一样的是，对于当前 dp[i]，我们此时决定是否抛弃后半部分的 dp[i + 1]。

同时我们写出对应的 rec[] 的方程:

也是和前面一样的，rec[i]决策变成了是否延续先前的 rec[i + 1] 所记录的对应右边界下标。

从后往前记录法动态演示

我们以 {4, -5, 8, 9, -19, 3, 6, -1, 10, -2} 为例

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

从后往前记录法实现代码

void Find_Subarray_Max2(int a[], int n) {
int *dp = new int[MAX]; //用于存储以下标为 i 作为开头的最大子数组累加和
int *rec = new int[MAX]; //用于记录下标为 i 作为开头的最大子数组的结尾下标
/* 动态规划部分 */
dp[n] = a[n];
rec[n] = n; //从最后开始
for(int i = n - 1; i >= 0 ; i--){
if(dp[i + 1] > 0){
dp[i] = a[i] + dp[i + 1];
rec[i] = rec[i + 1];
}else{
dp[i] = a[i]; //丢弃后半部分和为负的子段
rec[i] = i;
}
}
/* 还原最优解部分 */
int max = INT_MIN; //足够小的负数
int left, right;
for(int i = 0; i <= n; i++){
if(max max = dp[i];
left = i;
right = rec[i];
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] dp;
delete[] rec;
/* 作者 Amdeus */
}


时间复杂度

和前面一样的，依然是 O(n)。

两个优化点

状态转移过程的优化

在递推过程中，我们发现每一次更新当前区间范围最优解 dp[i] ，只用到了上一层的 dp[i - 1](或者 dp[i + 1])。那么我们是否可以不用 dp[] 数组呢？
答案是可以的。我们可以定义一个变量 sum，来一直记录当前子区间范围的最优解。这样可以省去 dp[] 数组，虽然我自己写代码时使用的动态分配存储空间的数组，后期能够回收内存空间。主要是对于不太会用这个技巧的童鞋，省去 dp[] 数组，可以节省一定的存储空间。?

还原最优解的优化

在上面的实现代码中，动态规划递推部分和还原最优解部分是分开的，那么是否可以同时进行呢？
我们借助状态转移优化中重新定义的变量 sum，同时在定义一个变量 max。max 是记录当前已经遍历到的地方为止的最优解，我们可以在 sumwww.yii666.com 被不断更新地同时，也不断更新 max。一直到整个数组被遍历完，此时 max 记录的自然是整个最大子段和问题的最优解。
因此我们可以得到如下的关系：

同时为了还原具体最优解， rec[] 也不能闲着，还是需要记录其边界。
若为从前往后记录，那么 rec[i] 在 sum > 0 时就等于 rec[i - 1]；在 sum <= 0 时就等于 i。并且还需要一个 right 不断记录右边界。
若为从后往前记录，那么 rec[i] 在 sum > 0 时就等于 rec[i + 1]；在 sum <= 0 时就等于 i。并且还需要一个
left 不断记录左边界。

优化后的两个写法思路实现代码

/* 从前往后 */
void Find_Subarray_Max3(int a[], int n){
int *rec = new int[MAX]; //用于记录下标为 i 作为结尾的最大子数组的开头下标
/* 省去dp数组存储 */
rec[0] = 0;
int sum = a[0], max = INT_MIN, right;
for(int i = 1; i <= n; i++){
if(sum > 0){
sum += a[i];
rec[i] = rec[i - 1]www.yii666.com;
}else{
sum = a[i]; //丢弃前半部分和为负的子段和
rec[i] = i;
}
/* 在过程中直接得到最优解 */
if(sum > max){
max = sum;
right = i; //可以获得右边界 rec记录对应左边界
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] rec;
}
/* 从后往前 */
void Find_Subarray_Max4(int a[], int n){
int *rec = new int[MAX]; //用于记录下标为 i 作为开头的最大子数组的结尾下标
/* 省去dp数组存储 */
rec[n] = n;
int sum = a[n], max = INT_MIN, left;
for(int i = n - 1; i >= 0; i--){
if(sum > 0){
sum += a[i];
rec[i] = rec[i + 1];
}else{
sum = a[i]; //丢弃后半部分和为负的子段和
rec[i] = i;
}
/* 在过程中直接得到最优解 */
if(sum > max){
max = sum;
left = i; //可以求得左边界 rec记录对应右边界
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] rec;
/* 作者 Amdeus */
}


时间复杂度

可以看到，我们少了一次循环，虽然算法时间复杂度依然是 O(n)，但实际上是少了 n 次扫描的。

完整程序

完整程序源代码

#include
using namespace std;
#define MAX 100
/* 从前往后 */
void Find_Subarray_Max1(int a[], int n){
int *dp = new int[MAX]; //用于存储以下标为 i 作为结尾的最大子数组累加和
int *rec = new int[MAX]; //用于记录下标为 i 作为结尾的最大子数组的开头下标
/* 动态规划部分 */
dp[0] = a[0];
rec[0] = 0; //从开头开始
for(int i = 1; i <= n; i++){
if(dp[i - 1] > 0){
dp[i] = a[i] + dp[i - 1];
rec[i] = rec[i - 1];
}else{
dp[i] = a[i]; //丢弃前部分和为负的子段
rec[i] = i;
}
}
/* 还原最优解部分 */
int max = INT_MIN; //足够小的负数
int left, right;
for(int i = 0; i <= n; i++){
if(max max = dp[i];
left = rec[i];
right = i;
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] dp;
delete[] rec;
}
/* 从后往前 */
void Find_Subarray_Max2(int a[], int n) {
int *dp = new int[MAX]; //用于存储以下标为 i 作为开头的最大子数组累加和
int *rec = new int[MAX]; //用于记录下标为 i 作为开头的最大子数组的结尾下标
/* 动态规划部分 */
dp[n] = a[n];
rec[n] = n; //从最后开始
for(int i = n - 1; i >= 0 ; i--){
if(dp[i + 1] > 0){
dp[i] = a[i] + dp[i + 1];
rec[i] = rec[i + 1];
}else{
dp[i] = a[i]; //丢弃后半部分和为负的子段
rec[i] = i;
}
}
/* 还原最优解部分 */
int max = INT_MIN; //足够小的负数
int left, right;
for(int i = 0; i <= n; i++){
if(max <文章来源站点https://www.yii666.com/; dp[i]){
max = dp[i];
left = i;
right = rec[i];
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] dp;
delete[] rec;
}
/* 从前往后（优化） */
void Find_Subarray_Max3(int a[], int n){
int *rec = new int[MAX]文章来源地址6554.html; //用于记录下标为 i 作为结尾的最大子数组的开头下标
/* 省去dp数组存储 */
rec[0] = 0;
int sum = a[0], max = INT_MIN, right;
for(int i = 1; i <= n; i++){
if(sum > 0){
sum += a[i];
rec[i] = rec[i - 1];
}else{
sum = a[i]; //丢弃前半部分和为负的子段和
rec[i] = i;
}
/* 在过程中直接得到最优解 */
if(sum > max){
max = sum;
right = i; //可以获得右边界 rec记录对应左边界
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] rec;
}
/* 从后往前 （优化） */
void Find_Subarray_Max4(int a[], int n){
int *rec = new int[MAX]; //用于记录下标为 i 作为开头的最大子数组的结尾下标
/* 省去dp数组存储 */
rec[n] = n;
int sum = a[n], max = INT_MIN, left;
for(int i = n - 1; i >= 0; i--){
if(sum > 0){
sum += a[i];
rec[i] = rec[i + 1];
}else{
sum = a[i]; //丢弃后半部分和为负的子段和
rec[i] = i;
}
/* 在过程中直接得到最优解 */
if(sum > max){
max = sum;
left = i; //可以求得左边界 rec记录对应右边界
}
}
cout<<"最大子数组累加和为: " < cout<<"起始下标为: " < delete[] rec;
}
main() {
int a[10] = {4, -5, 8, 9, -19, 3, 6, -1, 10, -2};
for(int i = 0; i <9; i++)
cout< cout< Find_Subarray_Max1(a, 9);
Find_Subarray_Max2(a, 9);
Find_Subarray_Max3(a, 9);
Find_Subarray_Max4(a, 9);
/* 作者 Amdeus */
}


程序运行结果

包含了两种写法思路实现的结果和优化后两种写法思路实现的结果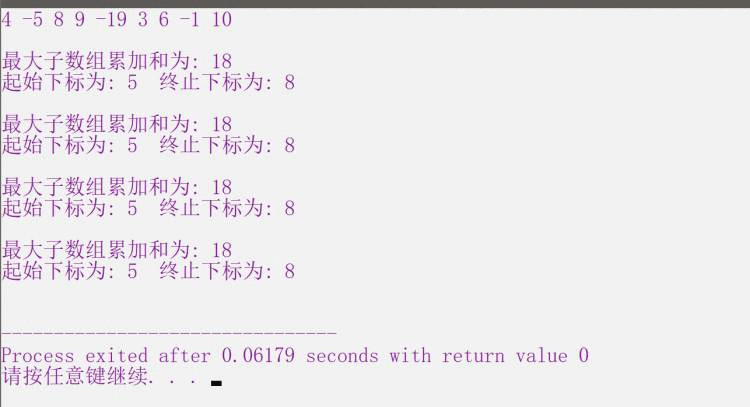

来源于：动态规划求解最大子段和 (两种写法+还原最优解)