配置Dlib环境&＃xff1a;  链接


1.计算积分

// The contents of this file are in the public domain. See LICENSE_FOR_EXAMPLE_PROGRAMS.txt
/*This example demonstrates the usage of the numerical quadrature function
integrate_function_adapt_simp(). This function takes as input a single variable
function, the endpoints of a domain over which the function will be integrated, and a
tolerance parameter. It outputs an approximation of the integral of this function over
the specified domain. The algorithm is based on the adaptive Simpson method outlined in:Numerical Integration method based on the adaptive Simpson method in
Gander, W. and W. Gautschi, "Adaptive Quadrature – Revisited,"
BIT, Vol. 40, 2000, pp. 84-101*/#include
#include
#include
#include using namespace std;
using namespace dlib;// Here we the set of functions that we wish to integrate and comment in the domain of
// integration.// x in [0,1]
double gg1(double x)
{return pow(e, x);
}// x in [0,1]
double gg2(double x)
{return x*x;
}// x in [0, pi]
double gg3(double x)
{return 1 / (x*x &＃43; cos(x)*cos(x));
}// x in [-pi, pi]
double gg4(double x)
{return sin(x);
}// x in [0,2]
double gg5(double x)
{return 1 / (1 &＃43; x*x);
}int main()
{// We first define a tolerance parameter. Roughly speaking, a lower tolerance will// result in a more accurate approximation of the true integral. However, there are // instances where too small of a tolerance may yield a less accurate approximation// than a larger tolerance. We recommend taking the tolerance to be in the// [1e-10, 1e-8] region.double tol &＃61; 1e-10;// Here we compute the integrals of the five functions defined above using the same // tolerance level for each.double m1 &＃61; integrate_function_adapt_simp(&gg1, 0.0, 1.0, tol);double m2 &＃61; integrate_function_adapt_simp(&gg2, 0.0, 1.0, tol);double m3 &＃61; integrate_function_adapt_simp(&gg3, 0.0, pi, tol);double m4 &＃61; integrate_function_adapt_simp(&gg4, -pi, pi, tol);double m5 &＃61; integrate_function_adapt_simp(&gg5, 0.0, 2.0, tol);// We finally print out the values of each of the approximated integrals to ten// significant digits.cout <<"\nThe integral of exp(x) for x in [0,1] is " <}

2.读取XML并显示

// The contents of this file are in the public domain. See LICENSE_FOR_EXAMPLE_PROGRAMS.txt
/*读取XML显示的一个程序
*/#include
#include
#include using namespace std;
using namespace dlib;// ----------------------------------------------------------------------------------------class doc_handler : public document_handler
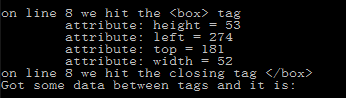
{/*As the parser runs it generates events when it encounters tags anddata in an XML file. To be able to receive these events all you have todo is make a class that inherits from dlib::document_handler andimplements its virtual methods. Then you simply associate aninstance of your class with the xml_parser.So this class is a simple example document handler that just printsall the events to the screen.*/
public:virtual void start_document(){cout <<"parsing begins" < tag" <" <};// ----------------------------------------------------------------------------------------int main(int argc, char** argv)
{try{// Check if the user entered an argument to this application. if (argc !&＃61; 2){cout <<"Please enter an xml file to parse on the command line" <}

先这样了&＃xff0c;本来只想看看Dlib的效果追踪咋样的&＃xff0c;结果一下子看到这么多有趣的东西……

接着去啃手势识别了…