垂直泊车路径设计

垂直泊车路径设计概述
垂直泊车涉及汽车从一个初始位置，通过精确控制横纵方向的移动，最终实现与车位垂直停放的过程。当汽车识别到合适的停车位后，必须执行路径规划，以确保汽车能够安全、高效地完成泊车。路径规划的核心在于制定最优的行驶路线，该路线需考虑泊车时间短、效率高、安全性强、乘坐舒适以及轮胎损耗低等因素。依据规划的路径，汽车的转向、刹车及驱动系统将协同工作，确保汽车沿预定路线平稳驶入车位，同时有效避让周围障碍物。下图展示了一个典型的垂直泊车路径实例。

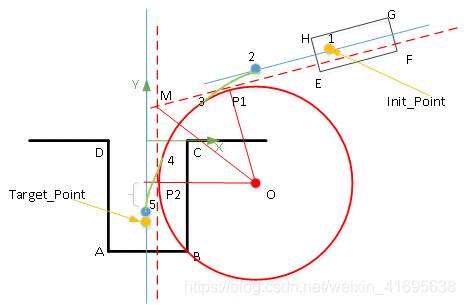
图1 垂直泊车路径设计示例
泊车路径通常由直线段、过渡曲线（用于平滑转向，减少轮胎磨损）和圆弧段组成。通过精准计算这些曲线，可确保汽车顺畅地完成泊车操作。

垂直泊车路径计算理论
2.1 单次入库计算方法
单次入库指的是汽车从起始位置直接倒车入库，中途无需调整方向。如图所示，汽车首先沿直线行驶，随后进入圆弧段，直至车身方向与车位平行时继续直线后退，直至完全停入车位，完成泊车。此过程中，圆弧的半径设定为汽车的最小转弯半径，这是因为在任何允许入库的其他半径条件下，使用最小转弯半径同样可行，只是接触点P1和P2的位置会有所不同。目标点Target_Point的位置确定为（0，l_r+Margin_Rear-L），其中l_r表示车辆后轴到车尾的距离，Margin_Rear为预留的安全距离，L为车位总长，W为车位宽，b为后轮间距。
基于回旋线理论，从直线段平滑过渡到圆弧段时，应在距离S/2处开始转向，从而确定转向启动点2和3。考虑到使用最小半径转向时，偏移量极小，几乎可以忽略，因此可得出如下的泊车路径。
为确保泊车过程顺利，需满足以下条件：

转向点2位于起始点1之后，即X_2

点G不应触及左侧边界；

点H不应触及车位边缘；

汽车不应碰撞到点C；

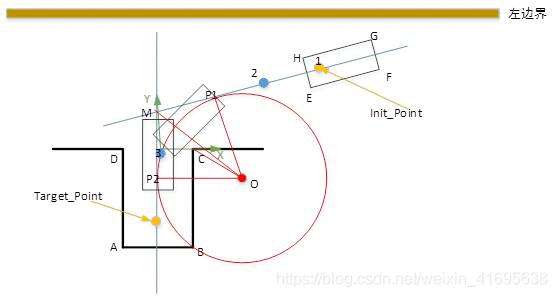
图2 单次入库路径示例
以下是各关键点的具体计算方法。
2.1.1 关键点计算
验证条件（1）和（2）的有效性，需计算两个切点P1和P2的坐标。已知直线L1: a_1 x+b_1 y+c_1=0；直线L2: x=0，可求得交点M的坐标为：
M（0，-c_1/b_1），其中a_1=tan(yaw_init)，b_1=-1，c_1=y_init-x_init*tan(yaw_init)
即：
M (0, y_init-x_init*tan(yaw_init))
由于∠P_1 MP_2 = π/2+yaw_init，因此有
∠OMP_2= ∠OMP_1= (π/2+yaw_init)/2
MP_1=MP_2=R_min cot(∠OMP_1)
OM=R_min/sin(∠OMP_1)
由此可得P_2的坐标为：
P_2 (0, M_y-MP_2)
P_1的坐标为：
P_1 (MP_1*cos(yaw_init), MP_1*sin(yaw_init))
圆心O的坐标为：
O (R_min, P_2_y)
根据回旋曲线理论，线段P_1-2和圆弧3-P_2的长度均为S/2，S = K*φ，其中φ代表最小半径对应的转向角度。因此，点2的坐标为：
2 (P_1_x+S/2*cos(yaw_init), P_1_y+S/2*sin(yaw_init))
点3的坐标可通过将点P_2围绕圆心O旋转S/2/R_min角度来计算：
3_x = O_x + (P_2_x- O_x) *cos(S/2/R_min) -(P_2_y- O_y) *sin(S/2/R_min)
3_y = O_y + (P_2_x- O_x) *sin(S/2/R_min) + (P_2_y- O_y) *cos(S/2/R_min)
3_yaw = π/2 - S/2/R_min
2.1.2 碰撞检测
为确保泊车安全，需进行碰撞检测，具体包括：
G点不碰左边界
如图，确保G点不触碰左侧边界，需满足条件：
R_G+MarginH点不碰库边
如图，确保H点不触碰左侧库边，需满足条件：
R_H+Margin车辆不碰C点
在整个泊车过程中，汽车后轴中心是离库点C最近的部分，为防止碰撞，需确保后轴中心右侧边界点I不与C点相撞：
3.2 多段式入库计算方法
当汽车无法一次性完成入库时，可能需要在库内外多次调整位置，直至成功入库。
...