作者:好kc好先生之家 | 来源:互联网 | 2024-10-15 14:09
题目链接题目大意:就是给你若干个点用一个最小的矩形把这些点覆盖掉就是给你若干个点用一个最小的矩形把这些点覆盖掉就是给你若干个点用一个最小的矩形把这些点覆盖掉解题思路&
题目链接
题目大意:
就是给你若干个点用一个最小的矩形把这些点覆盖掉就是给你若干个点用一个最小的矩形把这些点覆盖掉就是给你若干个点用一个最小的矩形把这些点覆盖掉
解题思路:
1.首先很明显我们可以对这些点求一个凸包,那么答案的矩形的一定是卡在凸包外面的1.首先很明显我们可以对这些点求一个凸包,那么答案的矩形的一定是卡在凸包外面的1.首先很明显我们可以对这些点求一个凸包,那么答案的矩形的一定是卡在凸包外面的
2.我们手动模一下就是逐渐增加凸包上面的点数,去看一下最小的矩形覆盖情况,就是矩形的一条边有两个点在上面就是和凸多边形一条边重合,其他三条边就卡在其他三个点上面。2.我们手动模一下就是逐渐增加凸包上面的点数,去看一下最小的矩形覆盖情况,就是矩形的一条边有两个点在上面就是和凸多边形一条边重合,其他三条边就卡在其他三个点上面。2.我们手动模一下就是逐渐增加凸包上面的点数,去看一下最小的矩形覆盖情况,就是矩形的一条边有两个点在上面就是和凸多边形一条边重合,其他三条边就卡在其他三个点上面。
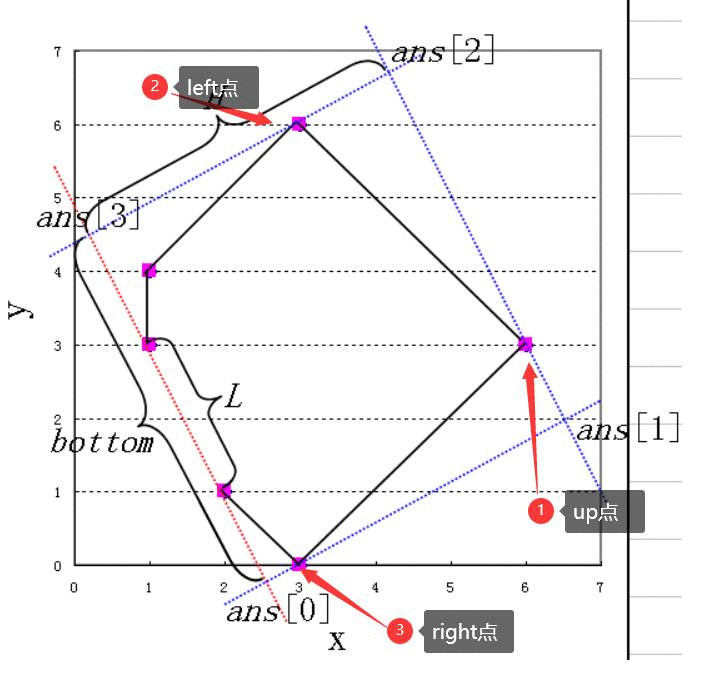
3.那么我们就可以O(n)枚举一下矩形卡着哪条边,我们通过用发现up点和bottem围成的三角形是一个单峰函数。left和right点的在bottom处的投影也是一个凹函数3.那么我们就可以O(n)枚举一下矩形卡着哪条边,我们通过用发现up点和bottem围成的三角形是一个单峰函数。left和right点的在bottom处的投影也是一个凹函数3.那么我们就可以O(n)枚举一下矩形卡着哪条边,我们通过用发现up点和bottem围成的三角形是一个单峰函数。left和right点的在bottom处的投影也是一个凹函数
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mid ((l + r) >> 1)
#define Lson rt <<1, l , mid
#define Rson rt <<1|1, mid &#43; 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define _for(i,a,b) for( int i &#61; (a); i <(b); &#43;&#43;i)
#define _rep(i,a,b) for( int i &#61; (a); i <&#61; (b); &#43;&#43;i)
#define for_(i,a,b) for( int i &#61; (a); i >&#61; (b); -- i)
#define rep_(i,a,b) for( int i &#61; (a); i > (b); -- i)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define hash Hash
#define next Next
#define f first
#define s second
using namespace std;
const int maxn &#61; 1e5 &#43; 10;
const double eps &#61; 1e-10;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;
struct Point
{double x, y;Point() {}Point(double x, double y) :x(x), y(y) {}
};
typedef Point Vector;
double minsqr &#61; 1e12;
int n;
Point ploy[maxn], sta[maxn], ans[10];
int dcmp(double x)
{if (fabs(x) < eps)return 0;else if (x > 0)return 1;return -1;
}
double Dot(Vector a, Vector b)
{return a.x*b.x &#43; a.y*b.y;
}
Vector operator &#43; (Vector a, Vector b)
{return Vector(a.x &#43; b.x, a.y &#43; b.y);
}
Vector operator - (Vector a, Vector b)
{return Vector(a.x - b.x, a.y - b.y);
}
Vector operator * (Vector a, double p)
{return Vector(a.x*p, a.y*p);
}
Vector operator / (Vector a, double p)
{return Vector(a.x / p, a.y / p);
}
double Distance(Point a, Point b)
{return sqrt((a.x - b.x)*(a.x - b.x) &#43; (a.y - b.y)*(a.y - b.y));
}
bool operator &#61;&#61; (const Point &a, const Point &b)
{return dcmp(a.x - b.x) &#61;&#61; 0 && dcmp(a.y - b.y) &#61;&#61; 0;
}bool operator<(Point a,Point b)
{if(!dcmp(a.y-b.y)) return a.x<b.x;return a.y<b.y;
}double Cross(Vector a, Vector b)
{return a.x*b.y - a.y*b.x;
}double DistanceToLine(Point A, Point M, Point N)
{return fabs(Cross(A - M, A - N) / Distance(M, N));
}double relation(Point A, Point B, Point C)
{return Dot(B - A, C - A) / Distance(A,B) / Distance(A,B);
}
Point pedal(Point A, Point B, Point C)
{double r &#61; relation(A,B,C);Point res;res.x &#61; A.x &#43; r * (B.x - A.x);res.y &#61; A.y &#43; r * (B.y - A.y);return res;
}bool cmp(Point a,Point b)
{if(!dcmp(a.x-b.x)) return a.y<b.y;return a.x<b.x;
}
int top &#61; 0;
void Graham() {sort(ploy,ploy&#43;n,cmp);for(int i &#61; 0; i < n; &#43;&#43; i) {while(top >&#61; 2 && dcmp(Cross(sta[top]-sta[top-1],ploy[i]-sta[top-1])) <&#61; 0) top--;sta[&#43;&#43;top] &#61; ploy[i];}int tmp &#61; top;for(int i &#61; n - 2; i >&#61; 0; -- i) {while(top >&#61; tmp &#43; 1 && dcmp(Cross(sta[top]-sta[top-1],ploy[i]-sta[top-1])) <&#61; 0) top--;sta[&#43;&#43; top] &#61; ploy[i];}top --;
}void qiake() {int left &#61; 1, right &#61; 1, up &#61; 1;for(int i &#61; 1; i <&#61; top; &#43;&#43; i) {while(dcmp(Cross(sta[i]-sta[up&#43;1],sta[i&#43;1]-sta[up&#43;1]) - Cross(sta[i]-sta[up],sta[i&#43;1]-sta[up])) >&#61; 0) up &#61; up % top &#43; 1;while(dcmp(Dot(sta[right&#43;1] - sta[i],sta[i&#43;1]-sta[i]) - Dot(sta[right]-sta[i],sta[i&#43;1]-sta[i])) >&#61; 0) right &#61; right % top &#43; 1;if(i &#61;&#61; 1) left &#61; right;while(dcmp(Dot(sta[i]-sta[i&#43;1],sta[left&#43;1]-sta[i&#43;1]) - Dot(sta[i]-sta[i&#43;1],sta[left]-sta[i&#43;1])) >&#61; 0) left &#61; left % top &#43; 1;double L &#61; DistanceToLine(sta[up],sta[i],sta[i&#43;1]);double Len &#61; Distance(sta[i],sta[i&#43;1]);double botten &#61; Dot(sta[right]-sta[i],sta[i&#43;1]-sta[i]) / Len &#43; Dot(sta[i]-sta[i&#43;1],sta[left]-sta[i&#43;1]) / Len - Len;if(dcmp(minsqr - botten * L) > 0) {minsqr &#61; botten * L;ans[0] &#61; pedal(sta[i],sta[i&#43;1],sta[right]);ans[1] &#61; pedal(ans[0],sta[right],sta[up]);ans[2] &#61; pedal(ans[1],sta[up],sta[left]);ans[3] &#61; pedal(sta[i],sta[i&#43;1],sta[left]);}}
}int main()
{IOS;cin >> n;for(int i &#61; 0; i < n; &#43;&#43; i) {double x, y;cin >> x >> y;ploy[i] &#61; (Point){x,y};}Graham();qiake();cout << fixed << setprecision(5) << minsqr << endl;int tmp &#61; 0;for(int i &#61; 0; i <&#61; 3; i &#43;&#43;)if(ans[i]<ans[tmp]) tmp &#61; i;for(int i &#61; 0; i < 4; &#43;&#43; i)cout << fixed << setprecision(5) << ans[(i &#43; tmp) % 4].x &#43; eps << " " << ans[(i &#43; tmp) % 4].y &#43; eps << endl;
}