ANSYS钢筋混凝土简支梁数值仿真

ANSYS钢筋混凝土简支梁数值仿真01

• 1.简支梁集中荷载模型
• 2.ANSYS模型和单元
• 3.钢筋混凝土材料属性
• • 3.1.混凝土材料参数
  • 3.2.钢筋材料参数
• 4.命令流
• • 4.1.无箍筋钢筋混凝土简支梁APDL数值分析
  • 4.2.有箍筋钢筋混凝土简支梁APDL数值分析
• 5.结果分析
• 6.参考文献

  如图1-1所示，钢筋混凝土简支梁，长5000mm，宽250mm，高600mm。混凝土截面布置两层钢筋，上层为2根直径25mm钢筋，下层为4根直径25mm钢筋。混凝土采用C50，钢筋全部采用HRB400，跨中集中荷载作用于一刚性垫板上，垫板尺寸为250mm×100mm。

  建立分离式有限元模型，混凝土采用SOLID65单元，钢筋采用LINK180单元，不考虑钢筋和混凝土之间的黏结滑移。创建分离式模型时，将几何实体以钢筋的位置切分，划分网格时将实体的边线定义为钢筋即可。加载点以均布荷载近似代替钢垫板，支座处采用线约束。暂不考虑模型的对称性，创建完整模型。单元尺寸取50mm。

  参照《混凝土结构设计规范》（GB50010-2010）规定的强度设计值。

3.1.混凝土材料参数

（1）混凝土轴心抗压强度标准值 f c k = 32.4 M P a f_{ck}=32.4MPa fck​=32.4MPa；
（2）混凝土轴心抗拉强度标准值 f t k = 2.64 M P a f_{tk}=2.64MPa ftk​=2.64MPa；
（3）混凝土轴心抗压强度设计值 f c = 23.1 M P a f_{c}=23.1MPa fc​=23.1MPa；
（4）混凝土轴心抗拉强度设计值 f t = 1.89 M P a f_{t}=1.89MPa ft​=1.89MPa。
（5）混凝土单轴应力应变关系受压段采用GB50010-2010规定的公式，不考虑下降段。
σ c = { f c [ 1 − ( 1 − ϵ c / ϵ 0 ) n ] , if  0 <ϵ c <ϵ 0   f c , if  ϵ 0 <ϵ c <ϵ c u \sigma_{c} = \begin{cases} f_{c}[1-(1-\epsilon_{c}/\epsilon_{0})^{n}], & \text{if $0<\epsilon_{c}<\epsilon_{0}$ } \\ f_{c} , & \text{if $\epsilon_{0}<\epsilon_{c}<\epsilon_{cu}$} \end{cases} σc​={ fc​[1−(1−ϵc​/ϵ0​)n],fc​,​if 0<ϵc​<ϵ0​ if ϵ0​<ϵc​<ϵcu​​
按照规范计算和规定取值 n = 2 n=2 n=2， ϵ 0 = 0.0020 \epsilon_{0}=0.0020 ϵ0​=0.0020， ϵ c u = 0.0033 \epsilon_{cu}=0.0033 ϵcu​=0.0033，上述曲线可以用一系列数据点拟合作为输入值，此处采用多线性等向强化模型MISO模拟。如图3-1所示，混凝土应力应变关系曲线。此处需要注意的是，混凝土弹性模量取值为应与混凝土的应力应变关系曲线的初始切线斜率一致。

（6）混凝土张开裂缝的剪力传递系数 β t = 0.5 \beta_{t}=0.5 βt​=0.5，闭合裂缝的剪力传递系数 β c = 0.95 \beta_{c}=0.95 βc​=0.95，拉应力释放系数采用缺省值 T c = 0.6 T_{c}=0.6 Tc​=0.6。

3.2.钢筋材料参数

（1）钢筋屈服强度标准值 f y k = 400 M P a f_{yk}=400MPa fyk​=400MPa；
（2）钢筋极限强度标准值 f s t k = 540 M P a f_{stk}=540MPa fstk​=540MPa；
（3）钢筋抗拉强度设计值 f y = 360 M P a f_{y}=360MPa fy​=360MPa；
（4）钢筋抗压强度设计值 f y ′ = 360 M P a f_{y}&＃8217;=360MPa fy′​=360MPa；
（5）钢筋的应力应变关系可采用理想弹塑性模型，为帮助收敛也可以采用具有强化阶段的弹塑性模型。此处采用双线性等向强化模型BISO模拟，如图3-2所示，钢筋应力应变关系曲线。

4.1.无箍筋钢筋混凝土简支梁APDL数值分析

!------------------------------------------------------------
!EX01.01 钢筋混凝土-简支梁-分离式模型-整体模型-数值分析
!单位制：国际单位制IS(m,s,Kg)
!------------------------------------------------------------
FINISH
/CLEAR
!------------------------------------------------------------
!Preprocessor
/PREP7
!Scalar Parameters
Pai=ACOS(-1)
!Element Type
ET,01,SOLID65,1,,,,,,1
ET,02,LINK180
!Real Constants
R,02,0.25*Pai*0.025*0.025
!Material Props
!Defines Elasticity Modulus
MP,EX,01,21.945E09
MP,EX,02,200.00E09
!Defines Poisson's Ratio
MP,PRXY,01,0.2
MP,PRXY,02,0.3
!Defines Concrete's Stress-Strain Relationship Curve
TB,MISO,01,01,12
TBPT,,0.0002,+23.10E+06*0.19 $TBPT,,0.0004,+23.10E+06*0.36
TBPT,,0.0006,+23.10E+06*0.51 $TBPT,,0.0008,+23.10E+06*0.64
TBPT,,0.0010,+23.10E+06*0.75 $TBPT,,0.0012,+23.10E+06*0.84
TBPT,,0.0014,+23.10E+06*0.91 $TBPT,,0.0016,+23.10E+06*0.96
TBPT,,0.0018,+23.10E+06*0.99 $TBPT,,0.0020,+23.10E+06*1.00
TBPT,,0.0030,+23.10E+06*1.00 $TBPT,,0.0033,+23.10E+06*1.00
!Defines Concrete's Failure Criterion
TB,CONCR,01
TBDATA,,0.5,0.95,1.89E+06,-1
!Defines Rebar's Stress-Strain Relationship Curve
TB,BISO,02
TBDATA,,360,0
!Modeling Create
BLC4,,,5.000,0.250,0.600
WPCSYS,-1 $WPROTA,,,90 $WPOFFS,,,2.450 $VSBW,ALL
WPCSYS,-1 $WPROTA,,,90 $WPOFFS,,,2.550 $VSBW,ALL
WPCSYS,-1 $WPROTA,,-90 $WPOFFS,,,0.050 $VSBW,ALL
WPCSYS,-1 $WPROTA,,-90 $WPOFFS,,,0.100 $VSBW,ALL
WPCSYS,-1 $WPROTA,,-90 $WPOFFS,,,0.150 $VSBW,ALL
WPCSYS,-1 $WPROTA,,-90 $WPOFFS,,,0.200 $VSBW,ALL
WPCSYS,-1 $WPOFFS,,,0.050 $VSBW,ALL $WPCSYS,-1
WPCSYS,-1 $WPOFFS,,,0.550 $VSBW,ALL $WPCSYS,-1
!------------------------------------------------------------
!Meshing Rebar
LSEL,S,LOC,Z,0.550 $LSEL,R,LOC,Y,0.050,0.200
LSEL,R,TAN1,Y $LSEL,U,LOC,Y,0.100,0.150
LPLOT
CM,RebarTop,LINE $LATT,02,02,02
LESIZE,ALL,0.050
LSEL,S,LOC,Z,0.050 $LSEL,R,LOC,Y,0.050,0.200
LSEL,R,TAN1,Y
LPLOT
CM,RebarBot,LINE $LATT,02,02,02
LESIZE,ALL,0.050
CMSEL,S,RebarTop $CMSEL,A,RebarBot
CM,Rebar,LINE
LMESH,ALL $LSEL,ALL
/ESHAPE,1 $EPLOT
!Meshing Concrete
VATT,01,,01 $MSHKEY,1 $ESIZE,0.050 $VMESH,ALL $ALLSEL,ALL
!Defines Constraints
LSEL,S,LOC,X,0.000 $LSEL,R,LOC,Z,0.000
LPLOT $DL,ALL,,ALL
LSEL,S,LOC,X,5.000 $LSEL,R,LOC,Z,0.000
LPLOT $DL,ALL,,UZ $DL,ALL,,UY
P0=25000 $Q0=P0/0.250/0.100
ASEL,S,LOC,X,2.450,2.550 $ASEL,R,LOC,Z,0.600
APLOT $SFA,ALL,1,PRES,Q0
ALLSEL,ALL
!Solve Current LS
/SOLU
ANTYPE,0
NSUBST,200
NEQIT,100
OUTRES,ALL,ALL
AUTOS,ON
CNVTOL,U,,0.02
SOLVE
!--------------------------------------------------------------------------
!General Postproc
/POST1
SET,LAST
!--------------------------------------------------------------------------
/DEVICE,VECTOR,OFF
PLDISP,1
ESEL,S,TYPE,,2
ETABLE,SAXL,LS,1
PLLS,SAXL,SAXL
ESEL,S,TYPE,,1
/DEVICE,VECTOR,ON
PLCRACK


4.2.有箍筋钢筋混凝土简支梁APDL数值分析

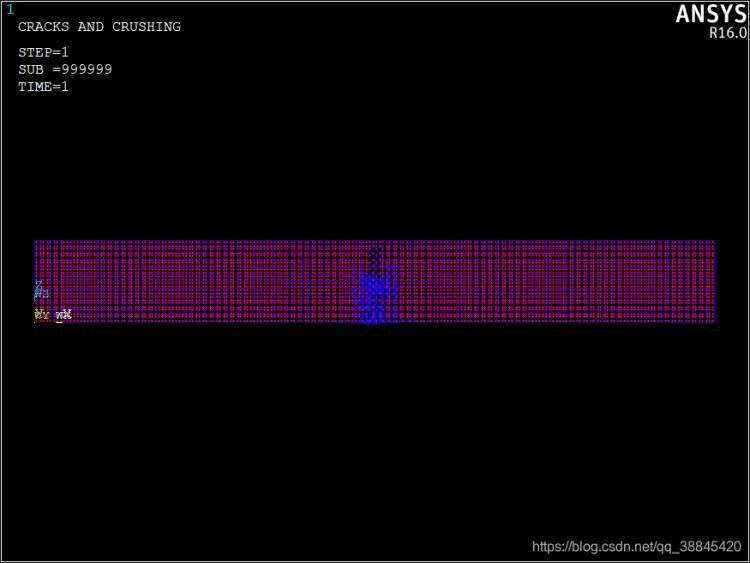
  从结果来说，这是一个糟糕的分析，一定有什么问题藏在某个让我不知道的地方，导致求解的最后一步不收敛，然后整个梁仿佛脆性断裂了一样，或者说脆性粉碎了。从产生细微裂缝到突然全部混凝土都坏掉了。
暂时还想不到原因所在，或许某天灵感来了就知道问题所在了，再来修正。

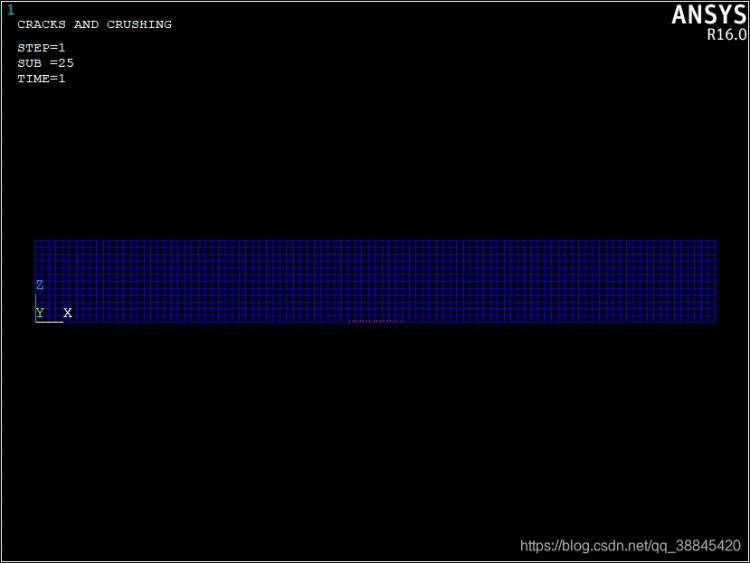
  我修改了SOLID65的KEYOPT参数，获得了新的结果。

[1] 王新敏. ANSYS工程结构数值分析[M]. 人民交通出版社, 2007.