基于FPGA的32位CRC校验码生成器设计与实现

大侠好&＃xff0c;欢迎来到FPGA技术江湖&＃xff0c;江湖偌大&＃xff0c;相见即是缘分。大侠可以关注FPGA技术江湖&＃xff0c;在“闯荡江湖”、"行侠仗义"栏里获取其他感兴趣的资源&＃xff0c;或者一起煮酒言欢。

今天给大侠带来基于FPGA 的CRC校验码生成器设计&＃xff0c;话不多说&＃xff0c;上货。

一、概述

CRC&＃xff0c;即Cyclic Redundancy Check&＃xff0c;循环冗余校验&＃xff0c;是一种数字通信中的常用信道编码技术。其特征是信息段和校验字段的长度可以任意选定。二、CRC校验的基本原理CRC码是由两部分组成的&＃xff0c;前部分是信息码&＃xff0c;就是需要校验的信息&＃xff0c;后部分是校验码&＃xff0c;如果CRC码长共n bit&＃xff0c;信息码长k bit&＃xff0c;就称为(n,k)码&＃xff0c;剩余的r bit即为校验位。如&＃xff1a;(7,3)码&＃xff1a;110 1001&＃xff0c;前三位110为信息码&＃xff0c;1001为校验码。三、校验码的生成规则1) 将原信息码左移r bit&＃xff0c;右侧补零&＃xff0c;如 110--> 110 0000&＃xff1b;2) 用110 0000除以g(x)  (注意&＃xff0c;使用的是模2除法&＃xff0c;见下文)&＃xff0c;得到的余数即为CRC校验码&＃xff1b;3) 将校验码续接到信息码的尾部&＃xff0c;形成CRC码。四、关于生成多项式g(x)在产生CRC校验码时&＃xff0c;要用到除法运算&＃xff0c;一般来说&＃xff0c;这是比较麻烦的&＃xff0c;因此&＃xff0c;把二进制信息预先转换成一定的格式&＃xff0c;这就是CRC的多项式表示。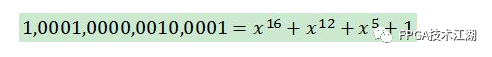二进制数表示为生成多项式的系数&＃xff0c;如下&＃xff1a;      所有二进制数均被表示为一个多项式&＃xff0c;x仅是码元位置的标记&＃xff0c;因此我们并不关心x的取值&＃xff0c;称之为码多项式。(我没研究过CRC代数推理过程&＃xff0c;没体会到用多项式计算的方便之处&＃xff0c;这里要学会的就是给出生成多项式g(x)&＃xff0c;能写出对应的二进制即可)常见的生成多项式如下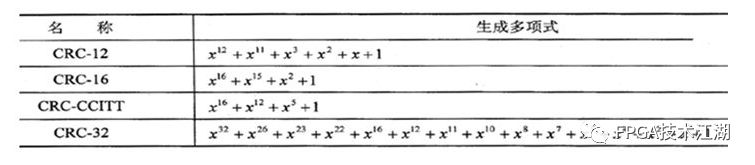&＃xff1a;五、关于模2除法模2运算就是加法不考虑进位&＃xff0c;减法不考虑借位。   1)加法运算&＃xff1a;     0&＃xff0b;0&＃xff1d;0        0&＃xff0b;1&＃xff1d;1        1&＃xff0b;0&＃xff1d;1        1&＃xff0b;1&＃xff1d;0例如0101&＃xff0b;0011&＃xff1d;0110&＃xff0c;列竖式计算&＃xff1a;
      　　　　0 1 0 1
 　　　　 &＃xff0b; 0 0 1 1
　　　　　　──────
     　　　　 0 1 1 02)减法运算&＃xff1a;      0&＃xff0d;0&＃xff1d;0        0&＃xff0d;1&＃xff1d;1        1&＃xff0d;0&＃xff1d;1        1&＃xff0d;1&＃xff1d;0  例如0110&＃xff0d;0011&＃xff1d;0101&＃xff0c;列竖式计算&＃xff1a;
    　　　　 0 1 1 0
　　　　 &＃xff0d;  0 0 1 1
　　　　  　──────
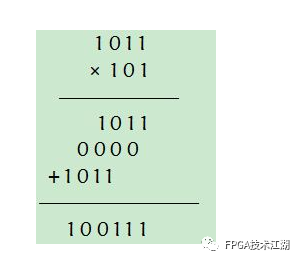
    　　　　 0 1 0 13)乘法运算0×0&＃xff1d;0        0×1&＃xff1d;0        1×0&＃xff1d;0        1×1&＃xff1d;1多位二进制模2乘法类似于普通意义上的多位二进制乘法&＃xff0c;不同之处在于后者累加中间结果时采用带进位的加法&＃xff0c;而模2乘法对中间结果的处理方式采用的是模2加法。例如1011×101&＃xff1d;100111&＃xff0c;列竖式计算&＃xff1a;   4)除法运算&＃xff1a;
       0÷1&＃xff1d;0        1÷1&＃xff1d;1多位二进制模2除法也类似于普通意义上的多位二进制除法&＃xff0c;但是在如何确定商的问题上两者采用不同的规则。后者按带借位的二进制减法&＃xff0c;根据余数减除数够减与否确定商1还是商0&＃xff0c;若够减则商1&＃xff0c;否则商0。多位模2除法采用模2减法&＃xff0c;不带借位的二进制减法&＃xff0c;因此考虑余数够减除数与否是没有意义的。实际上&＃xff0c;在CRC运算中&＃xff0c;总能保证除数的首位为1&＃xff0c;则模2除法运算的商是由余数首位与除数首位的模2除法运算结果确定。因为除数首位总是1&＃xff0c;按照模2除法运算法则&＃xff0c;那么余数首位是1就商1&＃xff0c;是0就商0。例如1100100÷1011&＃xff1d;1110……110&＃xff0c;列竖式计算&＃xff1a;掌握了上面的运算规则&＃xff0c;你可以尝试计算一个复杂一点的&＃xff0c;如下&＃xff1a;       如果得到的余数结果正确&＃xff0c;你掌握的东西就够用了。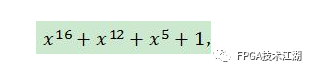六、CRC-CCITT的硬件实现CRC-CCITT的生成多项式为&＃xff1a;   对应的二进制数就是上面复杂运算中那个除数。由刚才的计算可知&＃xff0c;对于8 bit的数据 0xaa&＃xff0c;它的CRC校验码为0001 0100 1010 0000&＃xff0c;下面用verilog来实现&＃xff0c;看能否得到这个结果&＃xff1a;要实现这一过程&＃xff0c;仍然需要LFSR电路&＃xff0c;参看《FPGA设计中&＃xff0c;产生LFSR伪随机数》中关于该电路特性的介绍&＃xff0c;如果你不需要了解原理&＃xff0c;直接略过即可&＃xff1b;有所改进的地方就是&＃xff0c;可以将伪随机数发生器看作一个Moore型状态机&＃xff0c;它的输出只与当前的状态有关&＃xff1b;而此时利用LFSR电路&＃xff0c;需要引入数据输入端&＃xff0c;输出不仅取决于当前的状态&＃xff0c;还取决于输入信号&＃xff0c;相当于Mealy型状态机&＃xff0c;如下图&＃xff1a;  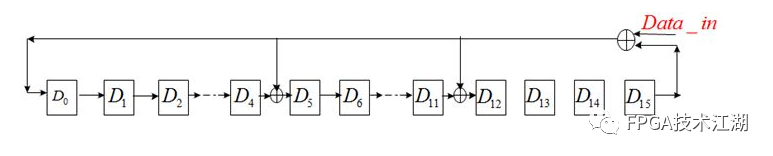注意对比与伪随机数产生器中该反馈支路的区别。反馈项gr&＃43;1gr……g0为生成多项式的系数&＃xff0c;依然是1代表存在反馈&＃xff0c;0代表不存在反馈&＃xff1b;此电路可以完成上述的模2除法操作&＃xff0c;若我们要求0xaa的CRC校验码&＃xff0c;则从高位到低位顺序输入0xaa共8 bit后&＃xff0c;D15……D0中的数据即为所要求的余数&＃xff0c;即CRC校验位。七、verilog描述如果用时序电路串行实现&＃xff0c;则8 bit数据要移位8次&＃xff0c;就需要8个clk&＃xff0c;效率低下&＃xff0c;为了能在一个时钟周期输出结果&＃xff0c;必须采用组合电路&＃xff0c;当然&＃xff0c;这是以空间换时间的方法&＃xff0c;由于使用了for循环8次&＃xff0c;直观的讲电路规模将扩大8倍。仿真结果如下&＃xff1a;得到的是数据0xaa和0xf0的CRC校验码&＃xff0c;为验证结果的正确性&＃xff0c;可以按照模2法则手工计算一下。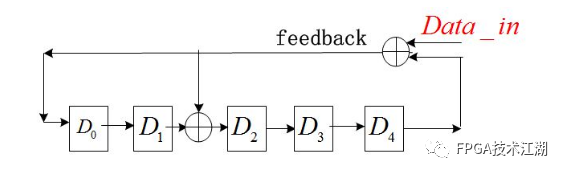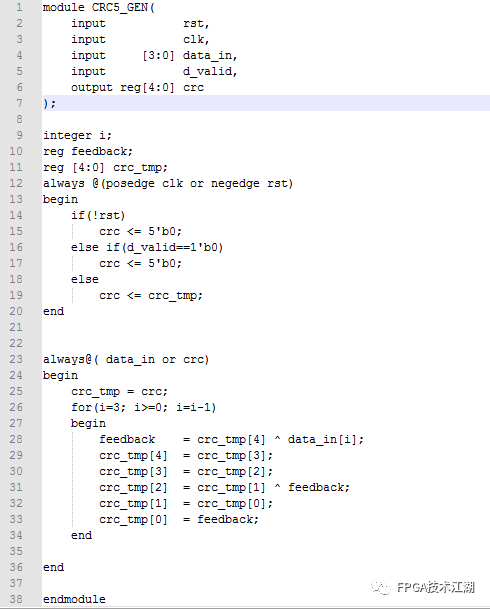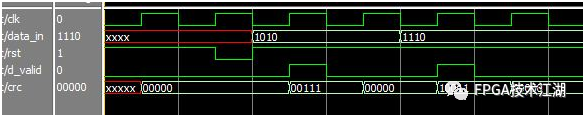八、其他例子同样给出一个4 bit信息位&＃xff0c;5 bitCRC码的(9&＃xff0c;4)码的程序和仿真结果&＃xff0c;程序的流程与上述流程完全一样&＃xff1a;       说明&＃xff1a;细心的大侠可能发现&＃xff0c;本篇对LFSR电路能完成模2求余操作的原因避而不谈&＃xff0c;不是因为不告诉你&＃xff0c;是因为目前也不是很清楚&＃xff0c;工科背景对数学推理实在是有点不知所云&＃xff0c;尤其是看到国内教材那好几页的公式的时候&＃xff0c;如果您有通俗易懂的讲解LFSR电路由来与应用的文章&＃xff0c;注意是深入浅出的&＃xff0c;请大力推荐&＃xff0c;在此感谢。END后续会持续更新&＃xff0c;带来Vivado、 ISE、Quartus II 、Candence等安装相关设计教程&＃xff0c;学习资源、项目资源、好文推荐等&＃xff0c;希望大侠持续关注。大侠们&＃xff0c;江湖偌大&＃xff0c;继续闯荡&＃xff0c;愿一切安好&＃xff0c;有缘再见&＃xff01;

往期推荐

• FPGA零基础学习&＃xff1a;VGA协议驱动设计

• FPGA零基础学习&＃xff1a;IIC协议驱动设计

• Zynq&＃xff1a;用PS控制DDR3内存读写

• 举例分析 Intel FPGA 和 Xilinx FPGA 的区别

• 新谈&＃xff1a;为什么你觉得FPGA难学&＃xff1f;如何入门&＃xff1f;

FPGA技术江湖广发江湖帖

无广告纯净模式&＃xff0c;给技术交流一片净土&＃xff0c;从初学小白到行业精英业界大佬等&＃xff0c;从军工领域到民用企业等&＃xff0c;从通信、图像处理到人工智能等各个方向应有尽有&＃xff0c;QQ微信双选&＃xff0c;FPGA技术江湖打造最纯净最专业的技术交流学习平台。

FPGA技术江湖微信交流群

加群主微信&＃xff0c;备注职业&＃43;方向&＃43;名字进群

FPGA技术江湖QQ交流群

备注地区&＃43;职业&＃43;方向&＃43;名字进群