当前位置: 开发笔记 > 编程语言 > 正文

10解析函数（四）

作者：helenheling2007895 | 来源：互联网 | 2024-10-14 11:10

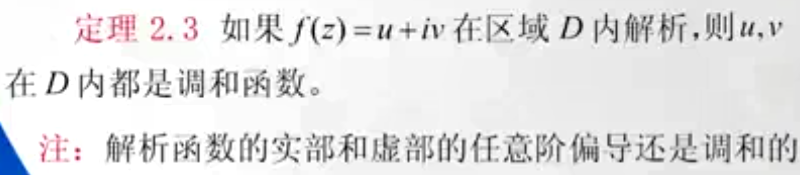
如果函数wf(z)u(x,y)iv(x,y)在某点只满足C-R条件，则不能确定f(z)在该点可导。解析函数的实部和虚部的任意阶偏导还是调和的，是因为解析

如果函数w&＃61;f(z)&＃61;u(x,y)&＃43;iv(x,y)在某点只满足C-R条件&＃xff0c;则不能确定f(z)在该点可导。

解析函数的实部和虚部的任意阶偏导还是调和的&＃xff0c;是因为解析函数的导数仍为解析函数。

解析函数的导数仍为解析函数这里先不忙证明&＃xff0c;只用下这个结论。

主要考察这二阶混合偏导的顺序能否交换。如果这两个二阶偏导连续它就可以交换。

运用结论可知三阶导函数存在&＃xff0c;二阶偏导连续的

推荐阅读

php
如何进行暂估入库的会计分录处理？

本文详细介绍了暂估入库的会计分录处理方法，包括账务处理的具体步骤和注意事项。 ... [详细]

蜡笔小新 2024-12-28 12:26:30
php
PHP 编程疑难解析与知识点汇总

本文详细解答了 PHP 编程中的常见问题，并提供了丰富的代码示例和解决方案，帮助开发者更好地理解和应用 PHP 知识。 ... [详细]

蜡笔小新 2024-12-28 12:22:34
go
优化ListView性能

本文深入探讨了如何通过多种技术手段优化ListView的性能，包括视图复用、ViewHolder模式、分批加载数据、图片优化及内存管理等。这些方法能够显著提升应用的响应速度和用户体验。 ... [详细]

蜡笔小新 2024-12-28 10:36:30
go
郑州大学在211高校中的地位与排名解析

本文将详细解读郑州大学作为一所位于河南省的211和双一流B类高校，在全国211高校中的地位与排名，帮助高三学生更好地了解这所知名学府的实力与发展前景。 ... [详细]

蜡笔小新 2024-12-28 10:08:34
int
深入理解 Oracle 存储函数：计算员工年收入

本文介绍如何使用 Oracle 存储函数查询特定员工的年收入。我们将详细解释存储函数的创建过程，并提供完整的代码示例。 ... [详细]

蜡笔小新 2024-12-28 09:49:42
int
优化ASM字节码操作：简化类转换与移除冗余指令

本文探讨如何利用ASM框架进行字节码操作，以优化现有类的转换过程，简化复杂的转换逻辑，并移除不必要的加0操作。通过这些技术手段，可以显著提升代码性能和可维护性。 ... [详细]

蜡笔小新 2024-12-28 09:35:00
jsp
2018回顾与2019展望

本文总结了2018年的关键成就，包括职业变动、购车、考取驾照等重要事件，并分享了读书、工作、家庭和朋友方面的感悟。同时，展望2019年，制定了健康、软实力提升和技术学习的具体目标。 ... [详细]

蜡笔小新 2024-12-28 09:10:26
jsp
电子元件封装库：三极管、MOS管及部分LDO（含3D模型）

本资源汇集了常用的插件和贴片三极管、MOS管以及部分LDO的封装，涵盖TO和SOT系列。所有封装均配有高质量的3D模型，共计96种，满足日常设计需求。 ... [详细]

蜡笔小新 2024-12-28 09:05:19
jsp
四载相伴，与51CTO学院共成长

在计算机技术的学习道路上，51CTO学院以其专业性和专注度给我留下了深刻印象。从2012年接触计算机到2014年开始系统学习网络技术和安全领域，51CTO学院始终是我信赖的学习平台。 ... [详细]

蜡笔小新 2024-12-28 08:20:07
jsp
CSS 布局：液态三栏混合宽度布局

本文介绍了如何使用 CSS 实现液态的三栏布局，其中各栏具有不同的宽度设置。通过调整容器和内容区域的属性，可以实现灵活且响应式的网页设计。 ... [详细]

蜡笔小新 2024-12-28 02:40:28
request
PHP检测AJAX请求的有效方法

本文详细介绍了如何使用PHP检测AJAX请求，通过分析预定义服务器变量来判断请求是否来自XMLHttpRequest。此方法简单实用，适用于各种Web开发场景。 ... [详细]

蜡笔小新 2024-12-27 21:20:10
request
小红书提高MCN机构入驻门槛，需缴纳20万元保证金

近期，小红书对MCN机构的入驻要求进行了调整，明确要求MCN机构在入驻时需缴纳20万元人民币的保证金。此举旨在进一步规范平台内容生态，确保社区的真实性和用户体验。 ... [详细]

蜡笔小新 2024-12-27 20:42:02
install
Linux 系统启动故障排除指南：MBR 和 GRUB 问题

本文详细介绍了 Linux 系统启动过程中常见的 MBR 扇区和 GRUB 引导程序故障及其解决方案，涵盖从备份、模拟故障到恢复的具体步骤。 ... [详细]

蜡笔小新 2024-12-27 20:40:29
install
动物餐厅高效获取小鱼干攻略

本文将介绍2023年动物餐厅中快速赚取小鱼干的有效方法，帮助玩家更轻松地积累资源。 ... [详细]

蜡笔小新 2024-12-27 20:33:20
go
Installing the MongoDB PHP Driver on XAMPP for macOS

This guide provides a comprehensive step-by-step approach to successfully installing the MongoDB PHP driver on XAMPP for macOS, ensuring a smooth and efficient setup process. ... [详细]

蜡笔小新 2024-12-27 19:58:25

helenheling2007895

这个家伙很懒，什么也没留下！

Tags | 热门标签

RankList | 热门文章