tensorflow学习笔记四——回归预测

本文基于tensorflow官网教程（https://tensorflow.google.cn/tutorials/keras/basic_regression）
机器环境：ubuntu14.04+tensorflow1.8.0
1.回归问题简介
回归（Regression）问题不同于分类问题，分类问题的输出域是离散的标签，而回归问题的输出
域是连续的。分类问题解决对输入的划分，如水果的分类、衣服的分类；而回归问题解决的是对
变化量的预测，如股票价格的预测、房价的预测等。本文的回归问题使用了波士顿房价数据集。
#coding=utf8
#包含模块
import tensorflow as tf
from tensorflow import keras
import numpy as np
#载入数据集
boston_housing=keras.datasets.boston_housing
(train_data,train_labels),(test_data,test_labels)=boston_housing.load_data()
#打乱顺序
order=np.argsort(np.random.random(train_labels.shape))
train_data=train_data[order]
train_labels=train_labels[order]
#打印数据集格式
print("Training set shape:{}".format(train_data.shape))
print("Test set shape:{}".format(test_data.shape))

训练集有404个数据，测试集有102个数据，每个数据都共享有13个特征。包括：

1.人均犯罪率2.住宅用地超过25000平方英尺的所占比例3.4....这些影响房价的因素
比如数据0的房价是a，人均犯罪率k1，住宅用地超过25000平方英尺所占比例为k2，因素3的值为
k3，...，因素13的值为k13，那么我们可以从这13个特征中分析其与房价a的关系，从而对一个新的
区域，只需要知道这13个特征的值，即可对其房价做出预测。
#打印单个数据
print("Train_data[0]:")
print(train_data[0])
print("Train_label[0]:")
print(train_labels[0])

可以看出，训练集数据0的数据为以上13个房价影响因素的值，标签为其房价
#使用pandas打印数据的值
#安装pandas $sudo apt-get install python-pandas
import pandas as pd
#定义房价影响因素的名称 如CRIM代表人均犯罪率
column_names=['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
                'TAX', 'PTRATIO', 'B', 'LSTAT']
df=pd.DataFrame(train_data,columns=column_names)
print(df.head())

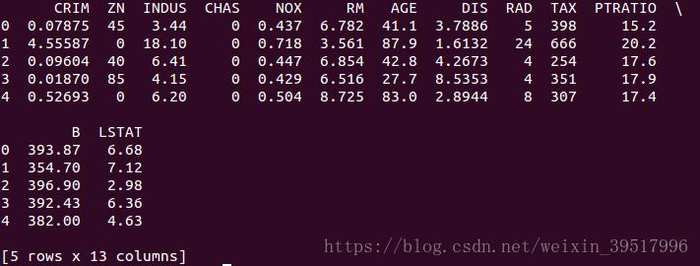
对输入数据进行规范化处理，不对输入数据进行规划处理，模型也能收敛，但是训练
过程更加困难，而且泛化能力不强
#数据的规范化处理
#求训练集均值
mean=train_data.mean(axis=0)
#求训练集标准差
std=train_data.std(axis=0)
#规范化处理 减去均值 再除以标准差
#注意求均值和标准差只用训练集数据，但是
#测试集同样要规范化处理
train_data=(train_data-mean)/std
test_data=(test_data-mean)/std
2.神经网络
#神经网络模型
def build_model():
    model=keras.Sequential([
keras.layers.Dense(64,activation=tf.nn.relu,input_shape=(train_data.shape[1],)),
keras.layers.Dense(64,activation=tf.nn.relu),keras.layers.Dense(1)])
    optimizer=tf.train.RMSPropOptimizer(0.001)
    model.compile(loss='mse',optimizer=optimizer,metrics=['mae'])
    return model
model=build_model()
model.summary()

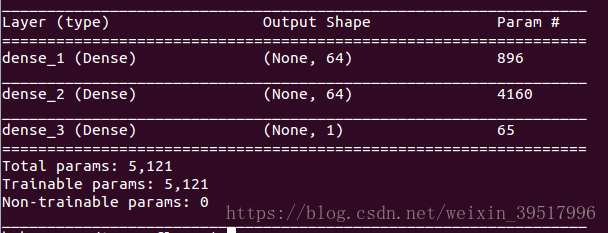
输入层为全连接层，64节点，**函数relu；隐藏层1为全连接层，64节点，**函数为
relu；输出层为全连接层，单个节点
#神经网络模型
def build_model():
    model=keras.Sequential([
keras.layers.Dense(64,activation=tf.nn.relu,input_shape=(train_data.shape[1],)),
keras.layers.Dense(64,activation=tf.nn.relu),keras.layers.Dense(1)])
    optimizer=tf.train.RMSPropOptimizer(0.001)
    model.compile(loss='mse',optimizer=optimizer,metrics=['mae'])
    return model
model=build_model()
model.summary()
#打印训练过程进度
#每个100训练轮的结束打印轮数
class PrintEpo(keras.callbacks.Callback):
    def on_epoch_end(self,epoch,logs):
        if (epoch+1) % 100 == 0: print(epoch+1)
#训练神经网络
EPOCHS=500
#将训练集以0.2的百分比划分训练集和验证集
history=model.fit(train_data,train_labels,epochs=EPOCHS,
validation_split=0.2,verbose=0,callbacks=[PrintEpo()])
#绘制训练过程损失
import matplotlib.pyplot as plt
def plot_history(history):
    plt.figure()
    plt.xlabel('Epoch')
    plt.ylabel('Mean Abs Error [1000$]')
    #绘制训练集损失
    plt.plot(history.epoch,np.array(history.history['mean_absolute_error']),
label='Train loss')
    #绘制验证集损失
    plt.plot(history.epoch,np.array(history.history['val_mean_absolute_error']),
label='Val loss')
    plt.legend()
    #限制y的取值
    plt.ylim([0,5])
plot_history(history)
plt.show()

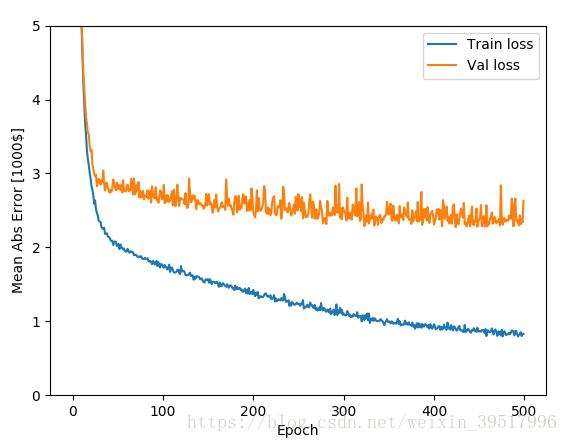
可以看出，200轮之后，神经网络在验证集上的损失减小得比较慢，因此在训练模型
时，可以通过回调函数指定模型的停止条件
#设置停止条件
early_stop=keras.callbacks.EarlyStopping(mOnitor='val_loss',patience=20)
#开始训练
history=model.fit(train_data,train_labels,epochs=EPOCHS,
validation_split=0.2,verbose=0,
callbacks=[early_stop,PrintEpo()])
#绘图
plot_history(history)
#打印训练过程loss变化
plt.show()

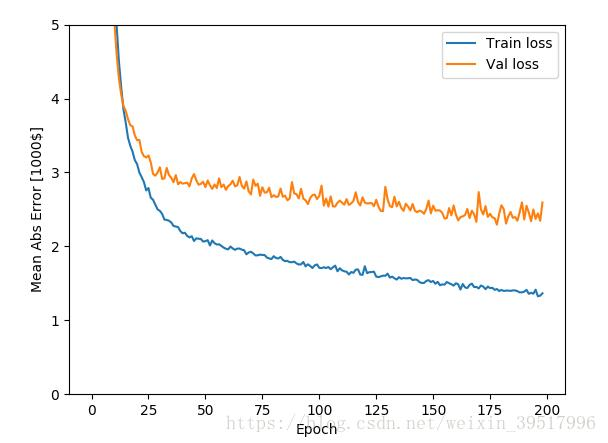
从图像中可以看出，平均误差收敛到$2500,与$15000相比，$2500不是个非常大的
偏差
#在测试集上验证误差
[loss,mae]=model.evaluate(test_data,test_labels,verbose=0)
#以7位浮点数打印平均绝对误差值
print("Testing set Mean Abs Error:${:7.2f}".format(mae*1000))