ngram_NGram

一、什么是N-Gram

　N-Gram是一种统计语言模型，用来根据前(n-1)个item来预测第n个item。在应用层面，这些item字符（输入法应用）等。一般来讲，可以从大规模文本或音频语料库生成N-Gram模型。 习惯上，1-gram叫unigram，2-gram称为bigram，3-gram是trigram。还有four-gram、five-gram等，不过大于n>5的应用很少见。

　N-Gram语言模型的思想，可以追溯到信息论大师香农的研究工作，他提出一个问题：给定一串字母，如”for ex”，下一个最大可能性出现的字母是什么。从训练语料数据中，我们可以通过极大似然估计的方法，得到N个概率分布：是a的概率是0.4，是b的概率是0.0001，是c的概率是…，当然，别忘记约束条件：所有的N个概率分布的总和为1

　N-Gram模型概率公式推导。根据条件概率和乘法公式：( P(B|A) = frac{P(A,B)}{P(A)} )，假设一个序列T由( A_1,A_2,A_3,...,A_n)组成，那么(P(T) )的概率为：

( P(A_1A_2A_3...A_n) = P(A_1)*P(A_2|A_1)*P(A_3|A_2,A_1)*...*P(A_n|A_1,A_2,...,A_{n-1}) )其中( P(A_1,A_2,...,A_{n-1}) > 0 )

　如果直接这么计算，是有很大困难的，需要引入马尔科夫假设，即：一个item的出现概率，只与其前m个items有关，当m=0时，就是unigram，m=1时，是bigram模型，m=2时，是trigram模型。例如当m=2时，上述(P(T) )的概率为：

( P(A_1A_2A_3...A_n) = P(A_1)*P(A_2|A_1)*P(A_3|A_2)*P(A_4|A_3)*...*P(A_n|A_{n-1}) )

　而( P(A_n|A_{n-1}) )条件概率可以通过极大似然估计求得，等于：( Count(A_{n-1},A_n)/Count(An-1) )

二、实例讲解N-Gram的一个应用 

　二元语言模型判断句子是否合理：假设现在有一个语料库，我们统计了下面的一些词出现的数量

　下面的这些概率值作为已知条件：

　( P(i | ) = 0.25, P(|food) = 0.68,P(want | ) = 0.25 )

　下面这个表给出的是基于Bigram模型进行计数之结果：

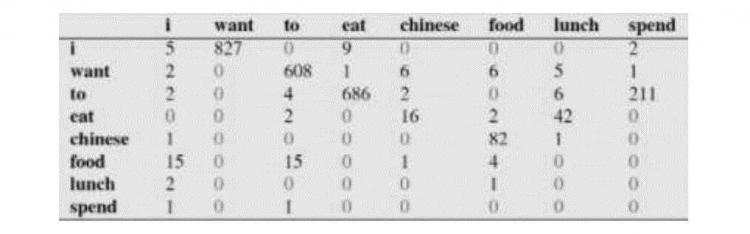
　例如，其中第一行，第二列表示给定前一个词是 “i” 时，当前词为“want”的情况一共出现了827次。据此，我们便可以算得相应的频率分布表如下：

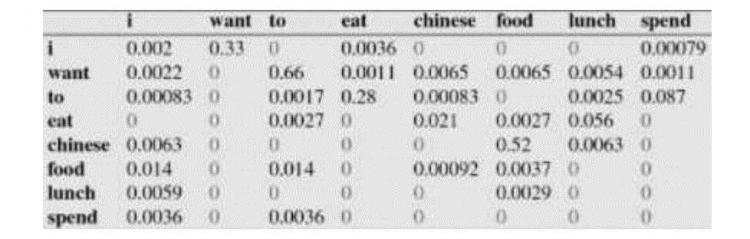
　比如说，我们就以表中的( P(eat|i)=0.0036 )这个概率值讲解，从表一得出“i”一共出现了2533次，而其后出现eat的次数一共有9次，( P(eat|i)=P(eat,i)/P(i)=count(eat,i)/count(i)=9/2533 = 0.0036 )

　下面我们通过基于这个语料库来判断s1=“ i want chinese food” 与s2 = " want i chinese food"哪个句子更合理：通过例子来讲解是最人性化的（其中涉及的概率查上表）

　首先来判断P(s1) ：( P(s1)=P(i|)P(want|i)P(chinese|want)P(food|chinese)P(|food)=0.25*0.33*0.0065*0.52*0.68 = 0.000189618)

　再来求P(s2)：( P(s2)=P(want|)P(i|want)P(chinese|want)P(food|chinese)P(|food) = 0.25*0.0022*0.0065*0.52*0.68 = 0.00000126412)

　通过比较我们可以明显发现P(s2) i want chinese food"更像人话。再深层次的分析，我们可以看到这两个句子的概率的不同，主要是由于顺序i want还是want i的问题，根据我们的直觉和常用搭配语法，i want要比want i出现的几率要大很多。所以两者的差异，第一个概率大，第二个概率小，也就能说的通了

　N-gram模型的一个常见应用

　　搜索引擎（Google或者Baidu）、或者输入法的猜想或者提示。你在用谷歌时，输入一个或几个词，搜索框通常会以下拉菜单的形式给出几个像下图一样的备选，这些备选其实是在猜想你想要搜索的那个词串。

　　再者，当你用输入法输入一个汉字的时候，输入法通常可以联系出一个完整的词，例如我输入一个“刘”字，通常输入法会提示我是否要输入的是“刘备”。通过上面的介绍，你应该能够很敏锐的发觉，这其实是以N-Gram模型为基础来实现的。比如下图：

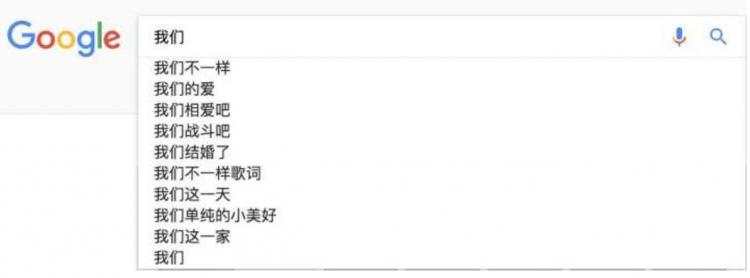
　　那么原理是什么呢？也就是我打入“我们”的时候，后面的“不一样”，”的爱“这些是怎么出来的，怎么排序的？实际上是根据语言模型得出。假如使用的是二元语言模型预测下一个单词：

　　排序的过程就是：p(”不一样“|"我们")>p(”的爱“|"我们")>p(”相爱吧“|"我们")>.......>p("这一家"|”我们“)，这些概率值的求法和上面提到的完全一样，数据的来源可以是用户搜索的log。

三、n-gram的n大小对性能的影响

　n越大，对下一个词出现的约束性信息更多，更大的辨别力，但是更稀疏，并且n-gram的总数也更多，为 V^n个（V为词汇表的大小）

　n越小，在训练语料库中出现的次数更多，更可靠的统计结果，更高的可靠性 ，但是约束信息更少，其中当N为特定值的时候，我们来看一下n-gram可能的总数，如下表：

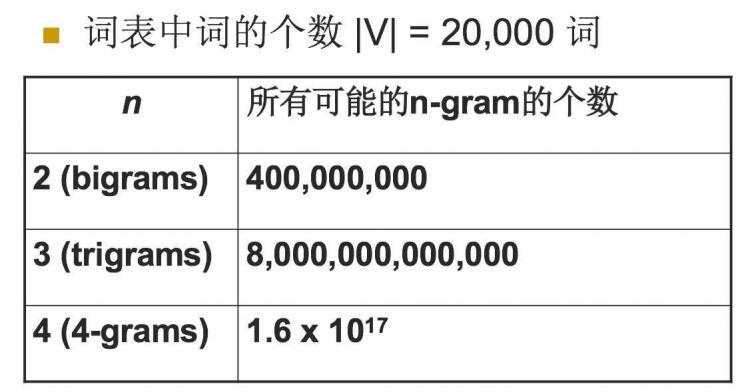
　对于上图，用一个例子来进行解释，加入目前词汇表中就只有三个单词，”我爱你“，那么bigram的总数是3^2=9个，有”我我“，我爱，我你，爱爱，爱你，爱我，你你，你我，你爱这9个，所以对应上面的表示是bigrams是20000^2=400,000,000，trigrams=20000^3 = 8,000,000,000,000

四、N-Gram模型的缺点

　不过，Ngram模型有其局限性：

　　首先，由于参数空间的爆炸式增长，它无法处理更长程的context（N > 3）N>3">

　　其次，它没有考虑词与词之间内在的联系性。例如，考虑"the cat is walking in the bedroom"这句话。如果我们在训练语料中看到了很多类似“the dog is walking in the bedroom”或是“the cat is running in the bedroom”这样的句子，那么，即使我们没有见过这句话，也可以从“cat”和“dog”（“walking”和“running”）之间的相似性，推测出这句话的概率。然而， Ngram模型做不到。这是因为，Ngram本质上是将词当做一个个孤立的原子单元去处理的。这种处理方式对应到数学上的形式是一个个离散的one-hot向量。例如，对于一个大小为5的词典：{"I", "love", "nature", "luaguage", "processing"}，“nature”对应的one-hot向量为：[0,0,1,0,0]，显然，one-hot向量的维度等于词典的大小。这在动辄上万甚至百万词典的实际应用中，面临着巨大的维度灾难问题。