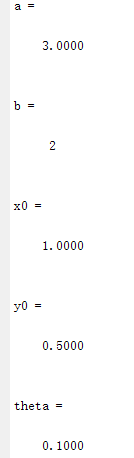matlab生成不同的椭圆,[平面几何][Matlab]平面椭圆参数与一般式之间的转换

椭圆的一般式为：\[A{x^2} + Bxy + C{y^2} + Dx + Ey + F = 0\]

椭圆的参数为：长半轴 $a$短半轴 $b$  椭圆中心 $(x_{0},y_{0})$  倾角为 $\theta$ (定义逆时针为正，长轴与x正方向的夹角)

1.由椭圆参数转化为一般式：

推导过程：

椭圆 $C[3*3]$ ,中心在原点，长轴与x轴重合，经过旋转矩阵  ${R} =f({\theta})$ , 平移矩阵 ${T}$$ =$$g$$(x_{0},y_{0})$,

后得到

$C^{&＃39;}=T^{T}*R^{T}*C*R*T$

ps:关于旋转矩阵R和平移矩阵T的定义看上篇博文 直角坐标系下点/曲线平移与旋转的矩阵计算

即 $H({\theta},x_{0},y_{0},a,b)=A{x^2} + Bxy + C{y^2} + Dx + Ey + F $

对应相等可以得到：

①$A = \frac{{{{\cos }^2}\theta }}{{{a^2}}} + \frac{{{{\sin }^2}\theta }}{{{b^2}}}$

② $B = 2 \cdot \sin \theta  \cdot \cos \theta  \cdot (\frac{1}{{{a^2}}} - \frac{1}{{{b^2}}})$

③ $C = \frac{{{{\cos }^2}\theta }}{{{b^2}}} + \frac{{{{\sin }^2}\theta }}{{{a^2}}}$

④ $D =  - 2 \cdot [{x_0} \cdot (\frac{{{{\cos }^2}\theta }}{{{a^2}}} + \frac{{{{\sin }^2}\theta }}{{{b^2}}}) + {y_0} \cdot \sin \theta  \cdot \cos \theta  \cdot (\frac{1}{{{a^2}}} - \frac{1}{{{b^2}}})]$

⑤ $E =  - 2 \cdot [{x_0} \cdot \sin \theta  \cdot \cos \theta  \cdot (\frac{1}{{{a^2}}} - \frac{1}{{{b^2}}}) + {y_0} \cdot (\frac{{{{\cos }^2}\theta }}{{{b^2}}} + \frac{{{{\sin }^2}\theta }}{{{a^2}}})]$

⑥$F = \frac{{{{({x_0} \cdot \cos \theta  + {y_0} \cdot \sin \theta )}^2}}}{{{a^2}}} + \frac{{{{({x_0} \cdot \sin \theta  - {y_0} \cdot \cos \theta )}^2}}}{{{b^2}}} - 1$

matlab推导过程

+验证

clc

syms a b theta x0 y0

% 公式推导

C = [1/a.^2 0 0;

0 1/b.^2 0;

0 0 -1;];

Rot = [cos(theta) sin(theta) 0;

-sin(theta) cos(theta) 0;

0 0 1;];

T = [1 0 -x0;

0 1 -y0;

0 0 1;];

C1 = T&＃39;*Rot&＃39;*C*Rot*T;

%公式验证

as = a*a;

bs = b*b;

coss = cos(theta).^2;

sins = sin(theta).^2;

cs = sin(theta)*cos(theta);

A =coss/as+sins/bs;

B =2*cs*(1/as-1/bs);

C = coss/bs +sins/as;

D = -(2*A*x0 +B*y0);

E = -(B*x0 +2*A*y0);

F = (x0*cos(theta)+y0*sin(theta)).^2/as+(x0*sin(theta)-y0*cos(theta)).^2/bs-1

a = 3;

b = 2;

x0 = 1;

y0 = 0.5;

theta = 0.1;

A = eval(A)

B = eval(B)

C = eval(C)

D = eval(D)

E = eval(E)

F = eval(F)

syms x y

f1 = ezplot( A*x^2+ C*y^2 +F + B*x*y + D*x +E*y,[-2,6],[-2,6]);

set(f1,&＃39;Color&＃39;,&＃39;r&＃39;,&＃39;LineWidth&＃39;,1.5)

xlim([-2,6])

ylim([-2,6])

axis equal

grid on

2.由一般式得到椭圆参数式：

椭圆的一般式为：\[A{x^2} + Bxy + C{y^2} + Dx + Ey + F = 0\]

由①②③式可以得到：

长半轴： $a^{2}=\frac{2}{A+C-\sqrt{B^{2}+(A-C)^{2}}}$

短半轴： $b^{2}=\frac{2}{A+C+\sqrt{B^{2}+(A-C)^{2}}}$

倾角：　 ${\theta} = arcsin({ sign(-B) \sqrt{\frac{(Aa^{2}-Cb^{2})a^{2}b^{2}}{a^{4}-b^{4}}}})$

偏移：alpha = cos(theta).^2/a^2+sin(theta).^2/b^2;

beta = sin(theta)*cos(theta)*(1/a^2-1/b^2);

gama = cos(theta).^2/b^2+sin(theta).^2/a^2;

y0 = (E/2 - beta*D/(2*alpha))/(beta^2/alpha - gama)

x0 = (-D/2 - beta*y0)/alpha

%接上面程序运行

aa = 2/(A+C-sqrt(B^2+(A-C).^2))

bb = 2/(A+C+sqrt(B^2+(A-C).^2))

if(bb > aa)

temp = aa;

aa = bb;

bb = temp;

end

theta

theta2 = asin(sign(-B)*sqrt((A*aa-C*bb)*aa*bb/(aa*aa-bb*bb)))

a = sqrt(aa)

b = sqrt(bb)

alpha = cos(theta).^2/a^2+sin(theta).^2/b^2;

beta = sin(theta)*cos(theta)*(1/a^2-1/b^2);

gama = cos(theta).^2/b^2+sin(theta).^2/a^2;

y0 = (E/2 - beta*D/(2*alpha))/(beta^2/alpha - gama)

x0 = (-D/2 - beta*y0)/alpha