java0.13==0.3_0.1+0.2===0.3?事情并没有那么简单！

前言

众所周知Javascript中0.1 + 0.2是不等于0.3的，这非常容易求证。如下图，在chrome控制台中显示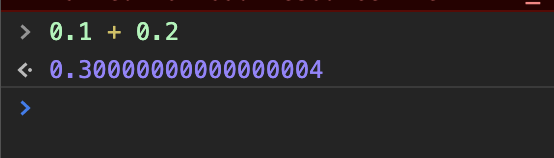

而且这似乎不是Javascript的问题。

在java中，输入0.1 + 0.2也是这个数，如下图：。

那问题来了：为什么计算机计算0.1+0.2会不等于0.3呢？

浮点数的存储方式

想要弄清楚这个问题，首先得清楚浮点型在计算机中是如何存储的。

1、浮点数转换成二进制，并采用科学计数法表示。

2、浮点型的存储实现是按照IEEE754标准的，可分为两种：

单精度--32位

双精度--64位

单精度浮点型存储

单精度浮点型存储，举个例子：

在十进制中，0.75用科学计数法可以表示为7.5 * 10^-1，同样在二进制中，0.75可以表示为：

0.75 = 1.1 * 2^-1

即：

0.75 = (1 * 2^0 + 1 * 2^-1)* 2 ^-1

其中幂次方-1用阶码表示，而基数1.1由于二进制整数部分都是1，所以去掉1留下0.1作为尾数部分(因为都是1点多的形式，所以没有必要存放1)。因此0.75在单精度浮点数是这样表示的：

阶码要加上一个基数，这个基数为2^(n-1) -1，n为阶码的位数，32位的阶码位是8位，所以这个基数为127，8位阶码能表示的最小整数位0，最大整数位255，所以能表示的指数范围为：-127~128，上面要表示的指数为-1，需要加上基数127，就变成126，如上图所示。

而尾数为0.1，所以尾数的最高位为1，后面的值填充0。

反过来，如果知道一个二进制的存储方式，同样地可以转换成10进制，如上结果为：

(1 + 1 * 2^-1) * 2^(126 - 127) = 1.5 * 2^-1 = 0.75

那么按照上面的理论，在二进制中0.1又该如何表示呢？

0.1无法被表示为这种方式，就像1/3无法在十进制中精确表示一样，在二进制中只能是用一个数尽可能的接近0.1。

双精度浮点型存储

Javascript的Number类型使用的是双精度浮点型，也就是C语言中的double类型。

因为C语言能够读取原始的内存信息，所以用C语言看看在双精度浮点型中0.1存储成什么样。(代码来自这Is there a printf converter to print in binary format?)

#include

void printBits(size_t const size, void const * const ptr)

{

unsigned char *b = (unsigned char*) ptr;

unsigned char byte;

int i, j;

for (i=size-1;i>=0;i--)

{

for (j=7;j>=0;j--)

{

byte = (b[i] >> j) & 1;

printf("%u", byte);

}

}

puts("");

}

int main (void)

{

double a = 0.1;

printBits(sizeof(a), &a);

return 0;

}

结果如下图所示：

双精度浮点数用11位表示阶码，52位表示尾数，如图所示

所以双精度的阶码基数为2^10 - 1 = 1023，0.1的阶码为01111111011，等于十进制1019，所以它的指数为-4，尾数约等于0.6

有了这个尾数再乘上指数，如图所示

也就是说0.1的实际存储要比0.1大。

0.2和0.1的区别在于0.2比0.1的阶码大了1，其他完全一样，也就是说0.2的实际存储也是偏大的。

所以0.1 + 0.2是大于0.3！

解决方法

解决方法有很多种，比如mathjs库、decimal.js等。这些库都很好的解决这个问题。

但如果只是涉及到比较简单的浮点型相加而去引用第三方库，无疑是用大炮打蚊子。

toFixed

在Javascript原生方法中提供了一个方法：Number.prototype.toFixed()

toFixed()方法使用定点表示法来格式化一个数

语法如下：

numObj.toFixed(digits)

其中参数digits是小数点后数字的个数：介于0到20之间。

返回的是一个数值的字符串形式，所以需要将结果强制转换为浮点型。

parseFloat((0.1 + 0.2).toFixed(10))//结果为0.3

parseFloat((0.3 / 0.1).toFixed(10)) // 结果为 3

parseFloat((0.7 * 180).toFixed(10))//结果为126

parseFloat((1.0 - 0.9).toFixed(10)) // 结果为 0.1

parseFloat((9.7 * 100).toFixed(10)) // 结果为 970

parseFloat((2.22 + 0.1).toFixed(10)) // 结果为 2.32

总结

计算机中使用IEEE754标准实现的浮点型存储都会有这个问题：用二进制来存储小数，而大部分小数转成二进制之后都是无限循环的值，因此存在取舍问题，也就是精度丢失。从而使得0.1 + 0.2 !== 0.3。

结尾

更多文章请移步楼主github,如果喜欢请点一下star,对作者也是一种鼓励。

关于找一找教程网

本站文章仅代表作者观点，不代表本站立场，所有文章非营利性免费分享。

本站提供了软件编程、网站开发技术、服务器运维、人工智能等等IT技术文章，希望广大程序员努力学习，让我们用科技改变世界。

[0.1+0.2===0.3?事情并没有那么简单！]http://www.zyiz.net/tech/detail-139750.html