根据README.md里面的说明,对于2D Pose SLAM部分的example学习记录。
比较简单的一个例子:
在二维平面上有一个移动机器人,有它移动3个点时记录下来的gps数据,和这三个点之间的odometry的数据。然后给定一个错误的初值,最后求得结果和前面设置的gps数据对比。
// Before we begin the example, we must create a custom unary factor to implement a
// "GPS-like" functionality. Because standard GPS measurements provide information
// only on the position, and not on the orientation, we cannot use a simple prior to
// properly model this measurement.
就是说用标准的gps是只有position坐标,没有orientation信息,所以就需要创建一个unaryFactor类。
具体代码如下:
class UnaryFactor: public NoiseModelFactor1
// The factor will hold a measurement consisting of an (X,Y) location
// We could this with a Point2 but here we just use two doubles
double mx_, my_;
public:
/// shorthand for a smart pointer to a factor
typedef boost::shared_ptr
// The constructor requires the variable key, the (X, Y) measurement value, and the noise model
UnaryFactor(Key j, double x, double y, const SharedNoiseModel& model):
NoiseModelFactor1
virtual ~UnaryFactor() {}
// Using the NoiseModelFactor1 base class there are two functions that must be overridden.
// The first is the 'evaluateError' function. This function implements the desired measurement
// function, returning a vector of errors when evaluated at the provided variable value. It
// must also calculate the Jacobians for this measurement function, if requested.
Vector evaluateError(const Pose2& q, boost::optional
{
// The measurement function for a GPS-like measurement is simple:
// error_x = pose.x - measurement.x
// error_y = pose.y - measurement.y
// Consequently, the Jacobians are:
// [ derror_x/dx derror_x/dy derror_x/dtheta ] = [1 0 0]
// [ derror_y/dx derror_y/dy derror_y/dtheta ] = [0 1 0]
if (H) (*H) &#61; (Matrix(2,3) <<1.0,0.0,0.0, 0.0,1.0,0.0).finished();
return (Vector(2) <
// The second is a &#39;clone&#39; function that allows the factor to be copied. Under most
// circumstances, the following code that employs the default copy constructor should
// work fine.
virtual gtsam::NonlinearFactor::shared_ptr clone() const {
return boost::static_pointer_cast
gtsam::NonlinearFactor::shared_ptr(new UnaryFactor(*this))); }
// Additionally, we encourage you the use of unit testing your custom factors,
// (as all GTSAM factors are), in which you would need an equals and print, to satisfy the
// GTSAM_CONCEPT_TESTABLE_INST(T) defined in Testable.h, but these are not needed below.
}; // UnaryFactor
比较简单&#xff0c;值得注意的是如果要继承NoiseModelFactor1&#xff0c;需要override两个函数evaluateError和clone。
int main(int argc, char** argv) {
// 1. Create a factor graph container and add factors to it
NonlinearFactorGraph graph;
// 2a. Add odometry factors
// For simplicity, we will use the same noise model for each odometry factor
noiseModel::Diagonal::shared_ptr odometryNoise &#61; noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
// Create odometry (Between) factors between consecutive poses
graph.emplace_shared
graph.emplace_shared
// 2b. Add "GPS-like" measurements
// We will use our custom UnaryFactor for this.
noiseModel::Diagonal::shared_ptr unaryNoise &#61; noiseModel::Diagonal::Sigmas(Vector2(0.1, 0.1)); // 10cm std on x,y
graph.emplace_shared
graph.emplace_shared
graph.emplace_shared
graph.print("\nFactor Graph:\n"); // print
// 3. Create the data structure to hold the initialEstimate estimate to the solution
// For illustrative purposes, these have been deliberately set to incorrect values
Values initialEstimate;
initialEstimate.insert(1, Pose2(0.5, 0.0, 0.2));
initialEstimate.insert(2, Pose2(2.3, 0.1, -0.2));
initialEstimate.insert(3, Pose2(4.1, 0.1, 0.1));
initialEstimate.print("\nInitial Estimate:\n"); // print
// 4. Optimize using Levenberg-Marquardt optimization. The optimizer
// accepts an optional set of configuration parameters, controlling
// things like convergence criteria, the type of linear system solver
// to use, and the amount of information displayed during optimization.
// Here we will use the default set of parameters. See the
// documentation for the full set of parameters.
LevenbergMarquardtOptimizer optimizer(graph, initialEstimate);
Values result &#61; optimizer.optimize();
result.print("Final Result:\n");
// 5. Calculate and print marginal covariances for all variables
Marginals marginals(graph, result);
cout <<"x1 covariance:\n" <
}
第一步创建graph&#xff1b;
第二步往graph里面添加odometry factor&#xff0c;添加GPS-like的factor&#xff1b;
第三步设置Values&#xff0c;初值initialEstimate&#xff0c;添加一些数&#xff1b;
第四步选择优化器&#xff0c;优化并输出结果。
Factor Graph:
size: 5
Factor 0: BetweenFactor(1,2)
measured: (2, 0, 0)
noise model: diagonal sigmas[0.2; 0.2; 0.1];
Factor 1: BetweenFactor(2,3)
measured: (3, 0, 0)
noise model: diagonal sigmas[0.2; 0.2; 0.1];
Factor 2: keys &#61; { 1 }
isotropic dim&#61;2 sigma&#61;0.1
Factor 3: keys &#61; { 2 }
isotropic dim&#61;2 sigma&#61;0.1
Factor 4: keys &#61; { 3 }
isotropic dim&#61;2 sigma&#61;0.1
Initial Estimate:
Values with 3 values:
Value 1: (N5gtsam5Pose2E) (0.5, 0, 0.2)
Value 2: (N5gtsam5Pose2E) (2.3, 0.1, -0.2)
Value 3: (N5gtsam5Pose2E) (4.1, 0.1, 0.1)
Final Result:
Values with 3 values:
Value 1: (N5gtsam5Pose2E) (-1.34728301e-14, 1.16725243e-15, -1.64808921e-16)
Value 2: (N5gtsam5Pose2E) (2, 2.17285499e-16, -7.22571183e-17)
Value 3: (N5gtsam5Pose2E) (5, -2.19538393e-16, -7.00766967e-17)
x1 covariance:
0.00828571429 2.76564799e-19 -7.47383061e-19
2.76564799e-19 0.00928571429 -0.00261904762
-7.47383061e-19 -0.00261904762 0.00706349206
x2 covariance:
0.00714285714 1.61131272e-19 1.17630708e-19
1.61131272e-19 0.00801587302 -0.00134920635
1.17630708e-19 -0.00134920635 0.00468253968
x3 covariance:
0.00828571429 1.35379321e-19 2.35144668e-19
1.35379321e-19 0.00968253968 0.00253968254
2.35144668e-19 0.00253968254 0.0146825397
可以看出&#xff0c;虽然在添加odometry和gps factor中添加了nosiy&#xff0c;但最后输出的结果是符合真实值的。
这个内容很简单&#xff0c;有一个2d平面&#xff0c;然后机器人在里面运行&#xff0c;记录了5个点之间的里程计信息。通过优化&#xff0c;求解它们相对于第一个点的坐标信息。
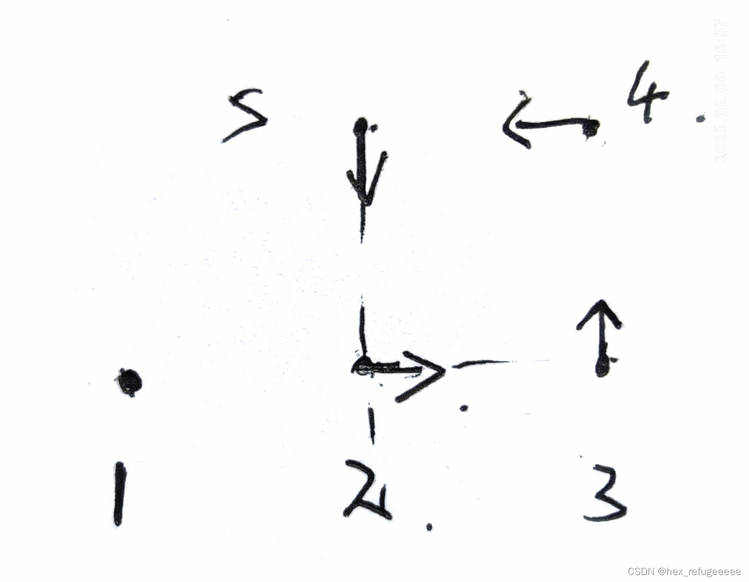
就是这个图的意思。
// 1. Create a factor graph container and add factors to it
NonlinearFactorGraph graph;
// 2a. Add a prior on the first pose, setting it to the origin
// A prior factor consists of a mean and a noise model (covariance matrix)
noiseModel::Diagonal::shared_ptr priorNoise &#61; noiseModel::Diagonal::Sigmas(Vector3(0.3, 0.3, 0.1));
graph.emplace_shared
// For simplicity, we will use the same noise model for odometry and loop closures
noiseModel::Diagonal::shared_ptr model &#61; noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
// 2b. Add odometry factors
// Create odometry (Between) factors between consecutive poses
graph.emplace_shared
graph.emplace_shared
graph.emplace_shared
graph.emplace_shared
// 2c. Add the loop closure constraint
// This factor encodes the fact that we have returned to the same pose. In real systems,
// these constraints may be identified in many ways, such as appearance-based techniques
// with camera images. We will use another Between Factor to enforce this constraint:
graph.emplace_shared
graph.print("\nFactor Graph:\n"); // print
包括创建第一个因子和回环限制因子。
// 3. Create the data structure to hold the initialEstimate estimate to the solution
// For illustrative purposes, these have been deliberately set to incorrect values
Values initialEstimate;
initialEstimate.insert(1, Pose2(0.5, 0.0, 0.2 ));
initialEstimate.insert(2, Pose2(2.3, 0.1, -0.2 ));
initialEstimate.insert(3, Pose2(4.1, 0.1, M_PI_2));
initialEstimate.insert(4, Pose2(4.0, 2.0, M_PI ));
initialEstimate.insert(5, Pose2(2.1, 2.1, -M_PI_2));
initialEstimate.print("\nInitial Estimate:\n"); // print
// 4. Optimize the initial values using a Gauss-Newton nonlinear optimizer
// The optimizer accepts an optional set of configuration parameters,
// controlling things like convergence criteria, the type of linear
// system solver to use, and the amount of information displayed during
// optimization. We will set a few parameters as a demonstration.
GaussNewtonParams parameters;
// Stop iterating once the change in error between steps is less than this value
parameters.relativeErrorTol &#61; 1e-5;
// Do not perform more than N iteration steps
parameters.maxIterations &#61; 100;
// Create the optimizer ...
GaussNewtonOptimizer optimizer(graph, initialEstimate, parameters);
// ... and optimize
Values result &#61; optimizer.optimize();
result.print("Final Result:\n");
与之前不同的是&#xff0c;多了对于优化器参数的设置部分。
简单明了&#xff0c;最容易理解的就是这个。 这个和二的Pose2SLAMExample.cpp区别不大&#xff0c;主要的区别是使用&#xff1a; 来代替了Pose2SLAMExample.cpp里面的数字1&#xff0c;2&#xff0c;3&#xff0c;4&#xff0c;5。 以及ExpressionFactorGraph来替代了NonlinearFactorGraph。 结果都一样&#xff1a; 读取g2o文件的内容然后直接输出计算&#xff0c;和前面的类似。 example中的源码部分使用了很多封装的函数比如readG2o&#xff0c;输入g2o文件名和3d标志位&#xff0c;输出已经将factor加入的graph和已经添加了的初值initial指针。 还有writeG2o函数&#xff1a; 其他部分和前面的一样&#xff0c;这里只是多了对于txt文件的读取和封装函数readG2o的使用。 完整源码&#xff1a; 原始部分没有对于加入graph的输出和初值initial的输出提示&#xff0c;我加了进去。 输出结果&#xff1a; 然后&#xff0c;我根据Pose2SLAMExampleExpressions.cpp的内容&#xff0c;使用这个noisyToyGraph.txt文件的内容&#xff0c;写了个类似的&#xff0c;手动输入值。 发现它们的结果不一样&#xff0c;不知道是哪里出现了问题。 主要是读取w100.graph文件内容的example&#xff0c;和前面没有太多的不同&#xff0c;有一个封装函数load2D&#xff0c; 输入graph_file文件和nosiy model&#xff0c;输出是已经将factor加入的graph和已经加入的初值initial。其它类似前面的。 这部分的主要内容和Pose2SLAMExample.cpp一模一样&#xff0c;它不同在于介绍了一个函数&#xff1a; 可以将获得的结果result存放在os文件中&#xff0c;并通过命令&#xff1a; 将它转换为PDF文件。 对比initial值&#xff1a; 优化的效果还是很明显的。 我利用这个函数和命令把前面w100.graph的优化结果也显示了一下&#xff1a; 这个好像是创造一系列的3D poses&#xff0c;每个pose都加入噪声&#xff0c;然后就优化&#xff1f; // Create N 3D poses, add relative motion between each consecutive poses. (The // relative motion is simply a unit translation(1, 0, 0), no rotation). For each // each pose, add some random noise to the x value of the translation part. // Use gtsam to create a prior factor for the first pose and N-1 between factors // and run optimization. 比较简单&#xff0c;对于initial部分的添加偏差值得学习一下&#xff1a; 使用了PCG solver来求解&#xff0c;其他内容和Pose2SLAMExample.cpp部分一样。 就是使用了sub PCG的求解&#xff0c;具体为什么使用这个不太清楚。 // 5. Calculate and print marginal covariances for all variables
cout.precision(3);
Marginals marginals(graph, result);
cout <<"x1 covariance:\n" <结果&#xff1a;
Final Result:
Values with 5 values:
Value 1: (N5gtsam5Pose2E) (-1.27455483e-20, 8.10527674e-20, 3.07189987e-20)
Value 2: (N5gtsam5Pose2E) (2, 1.78514217e-19, 4.34262714e-20)
Value 3: (N5gtsam5Pose2E) (4, -3.42173202e-11, 1.57079633)
Value 4: (N5gtsam5Pose2E) (4, 2, 3.14159265)
Value 5: (N5gtsam5Pose2E) (2, 2, -1.57079633)
三、Pose2SLAMExampleExpressions.cpp // Create Expressions for unknowns
Pose2_ x1(1), x2(2), x3(3), x4(4), x5(5); ExpressionFactorGraph graph; Final Result:
Values with 5 values:
Value 1: (N5gtsam5Pose2E) (1.49017327e-20, -2.14141805e-20, -4.58273596e-21)
Value 2: (N5gtsam5Pose2E) (2, -4.0097066e-20, -4.40676513e-21)
Value 3: (N5gtsam5Pose2E) (4, -4.9189295e-12, 1.57079633)
Value 4: (N5gtsam5Pose2E) (4, 2, -3.14159265)
Value 5: (N5gtsam5Pose2E) (2, 2, -1.57079633)
四、Pose2SLAMExample_g2o.cpp boost::tie(graph, initial) &#61; readG2o(g2oFile,is3D); /**
* &#64;brief This function parses a g2o file and stores the measurements into a
* NonlinearFactorGraph and the initial guess in a Values structure
* &#64;param filename The name of the g2o file\
* &#64;param is3D indicates if the file describes a 2D or 3D problem
* &#64;param kernelFunctionType whether to wrap the noise model in a robust kernel
* &#64;return graph and initial values
*/
GTSAM_EXPORT GraphAndValues readG2o(const std::string& g2oFile, const bool is3D &#61; false,
KernelFunctionType kernelFunctionType &#61; KernelFunctionTypeNONE);/**
* &#64;brief This function writes a g2o file from
* NonlinearFactorGraph and a Values structure
* &#64;param filename The name of the g2o file to write
* &#64;param graph NonlinearFactor graph storing the measurements
* &#64;param estimate Values
*/
GTSAM_EXPORT void writeG2o(const NonlinearFactorGraph& graph,
const Values& estimate, const std::string& filename);#include
#include
#include
#include
#include
using namespace std;
using namespace gtsam;
// HOWTO: ./Pose2SLAMExample_g2o inputFile outputFile (maxIterations) (tukey/huber)
int main(const int argc, const char *argv[]) {
string kernelType &#61; "none";
int maxIterations &#61; 100; // default
string g2oFile &#61; findExampleDataFile("noisyToyGraph.txt"); // default
// Parse user&#39;s inputs
if (argc > 1){
g2oFile &#61; argv[1]; // input dataset filename
// outputFile &#61; g2oFile &#61; argv[2]; // done later
}
if (argc > 3){
maxIterations &#61; atoi(argv[3]); // user can specify either tukey or huber
}
if (argc > 4){
kernelType &#61; argv[4]; // user can specify either tukey or huber
}
// reading file and creating factor graph
NonlinearFactorGraph::shared_ptr graph;
Values::shared_ptr initial;
bool is3D &#61; false;
if(kernelType.compare("none") &#61;&#61; 0){
boost::tie(graph, initial) &#61; readG2o(g2oFile,is3D);
}
if(kernelType.compare("huber") &#61;&#61; 0){
std::cout <<"Using robust kernel: huber " <
}
if(kernelType.compare("tukey") &#61;&#61; 0){
std::cout <<"Using robust kernel: tukey " <
}
// Add prior on the pose having index (key) &#61; 0
NonlinearFactorGraph graphWithPrior &#61; *graph;
noiseModel::Diagonal::shared_ptr priorModel &#61; //
noiseModel::Diagonal::Variances(Vector3(1e-6, 1e-6, 1e-8));
graphWithPrior.add(PriorFactor
std::cout <<"Adding prior on pose 0 " <
GaussNewtonParams params;
params.setVerbosity("TERMINATION");
if (argc > 3) {
params.maxIterations &#61; maxIterations;
std::cout <<"User required to perform maximum " <
std::cout <<"initial data: " <
std::cout <<"Optimizing the factor graph" <
Values result &#61; optimizer.optimize();
std::cout <<"Optimization complete" <
result.print("result");
} else {
const string outputFile &#61; argv[2];
std::cout <<"Writing results to file: " <
Values::shared_ptr initial2;
boost::tie(graphNoKernel, initial2) &#61; readG2o(g2oFile);
writeG2o(*graphNoKernel, result, outputFile);
std::cout <<"done! " <
return 0;
}Factor Graph:
size: 6
Factor 0: BetweenFactor(0,1)
measured: (0.774115, 1.18339, 1.57617)
noise model: unit (3)
Factor 1: BetweenFactor(1,2)
measured: (0.869231, 1.03188, 1.57942)
noise model: unit (3)
Factor 2: BetweenFactor(2,3)
measured: (1.35784, 1.03426, 1.56646)
noise model: unit (3)
Factor 3: BetweenFactor(2,0)
measured: (0.303492, 1.86501, -3.1139)
noise model: unit (3)
Factor 4: BetweenFactor(0,3)
measured: (-0.928526, 0.993695, -1.56354)
noise model: unit (3)
Factor 5: PriorFactor on 0
prior mean: (0, 0, 0)
noise model: diagonal sigmas[0.001; 0.001; 0.0001];
initial data:
Initial Estimate:
Values with 4 values:
Value 0: (N5gtsam5Pose2E) (0, 0, 0)
Value 1: (N5gtsam5Pose2E) (0.774115, 1.183389, 1.576173)
Value 2: (N5gtsam5Pose2E) (-0.26242, 2.047059, -3.127594)
Value 3: (N5gtsam5Pose2E) (-1.605649, 0.993891, -1.561134)
Optimizing the factor graph
Warning: stopping nonlinear iterations because error increased
errorThreshold: 0.0685034665 absoluteDecrease: -2.28853697639e-05 relativeDecrease: -0.000334187727181 iterations: 3 >? 100
Optimization complete
resultValues with 4 values:
Value 0: (N5gtsam5Pose2E) (-7.53875248522e-23, -3.04401700725e-24, 1.41745664019e-24)
Value 1: (N5gtsam5Pose2E) (0.956178940406, 1.14319822891, 1.54150026689)
Value 2: (N5gtsam5Pose2E) (0.126611466178, 1.9817945338, -3.08397402066)
Value 3: (N5gtsam5Pose2E) (-1.05038303244, 0.935131621066, -1.54052801033)#include
#include
#include
#include
#include
#include
#include
using namespace std;
using namespace gtsam;
int main(int argc, char** argv)
{
ExpressionFactorGraph graph;
Pose2_ x1(1), x2(2), x3(3), x4(4);
noiseModel::Diagonal::shared_ptr priorNoise &#61; noiseModel::Diagonal::Sigmas(Vector3(0.3, 0.3, 0.1));
graph.addExpressionFactor(x1, Pose2(0, 0, 0), priorNoise);
noiseModel::Diagonal::shared_ptr model &#61; noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
graph.addExpressionFactor(between(x1,x2), Pose2(0.774115, 1.183389, 1.576173), model);
graph.addExpressionFactor(between(x2,x3), Pose2(0.869231, 1.031877, 1.579418), model);
graph.addExpressionFactor(between(x3,x4), Pose2(1.357840, 1.034262, 1.566460), model);
graph.addExpressionFactor(between(x3,x1), Pose2(0.303492, 1.865011, -3.113898), model);
graph.addExpressionFactor(between(x1,x4), Pose2(-0.928526, 0.993695, -1.563542), model);
graph.print("\nFactor Graph:\n"); // print
Values initialEstimate;
initialEstimate.insert(1, Pose2(0.0, 0.0, 0.0 ));
initialEstimate.insert(2, Pose2(0.774115, 1.183389, 1.576173 ));
initialEstimate.insert(3, Pose2(-0.262420, 2.047059, -3.127594));
initialEstimate.insert(4, Pose2(-1.605649, 0.993891, -1.561134 ));
initialEstimate.print("\nInitial Estimate:\n"); // print
GaussNewtonParams parameters;
parameters.relativeErrorTol &#61; 1e-5;
parameters.maxIterations &#61; 3;
GaussNewtonOptimizer optimizer(graph, initialEstimate, parameters);
Values result &#61; optimizer.optimize();
result.print("Final Result:\n");
return 0;
}//我自己写的
Values with 4 values:
Value 1: (N5gtsam5Pose2E) (-2.22725181e-16, 4.72511144e-17, 2.13599316e-17)
Value 2: (N5gtsam5Pose2E) (0.986584345, 1.13382604, 1.56093936)
Value 3: (N5gtsam5Pose2E) (0.175794601, 1.96362262, -3.12403007)
Value 4: (N5gtsam5Pose2E) (-1.04609988, 0.949686099, -1.56055604)
//使用Pose2SLAMExample_g2o.cpp输出的
resultValues with 4 values:
Value 0: (N5gtsam5Pose2E) (-7.53875248522e-23, -3.04401700725e-24, 1.41745664019e-24)
Value 1: (N5gtsam5Pose2E) (0.956178940406, 1.14319822891, 1.54150026689)
Value 2: (N5gtsam5Pose2E) (0.126611466178, 1.9817945338, -3.08397402066)
Value 3: (N5gtsam5Pose2E) (-1.05038303244, 0.935131621066, -1.54052801033)
五、Pose2SLAMExample_graph.cpp boost::tie(graph, initial) &#61; load2D(graph_file, model);
六、Pose2SLAMExample_graphviz.cpp // save factor graph as graphviz dot file
// Render to PDF using "fdp Pose2SLAMExample.dot -Tpdf > graph.pdf"
ofstream os("Pose2SLAMExample.dot");
graph.saveGraph(os, result);fdp Pose2SLAMExample.dot -Tpdf > graph.pdf 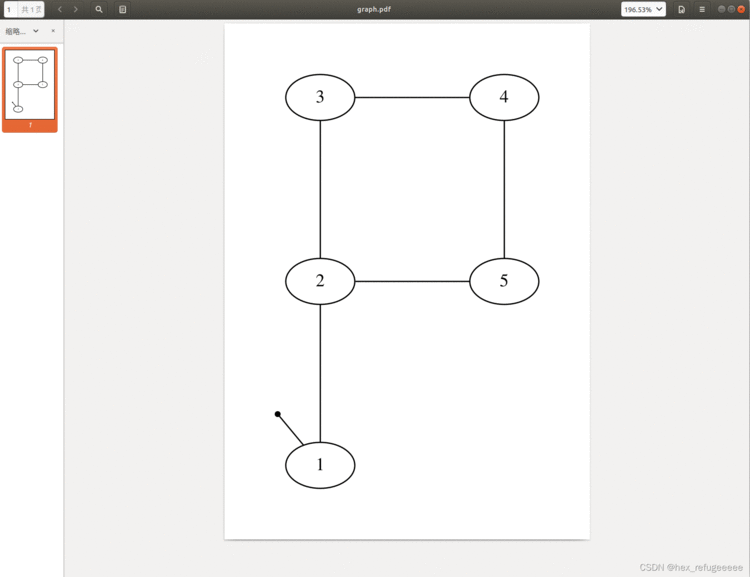
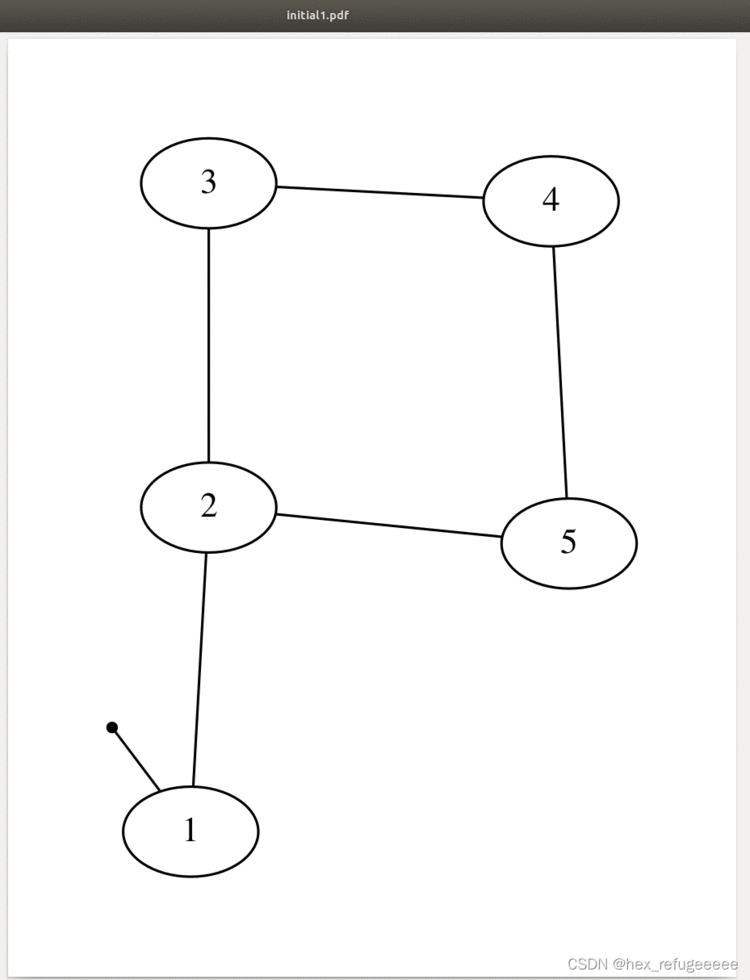
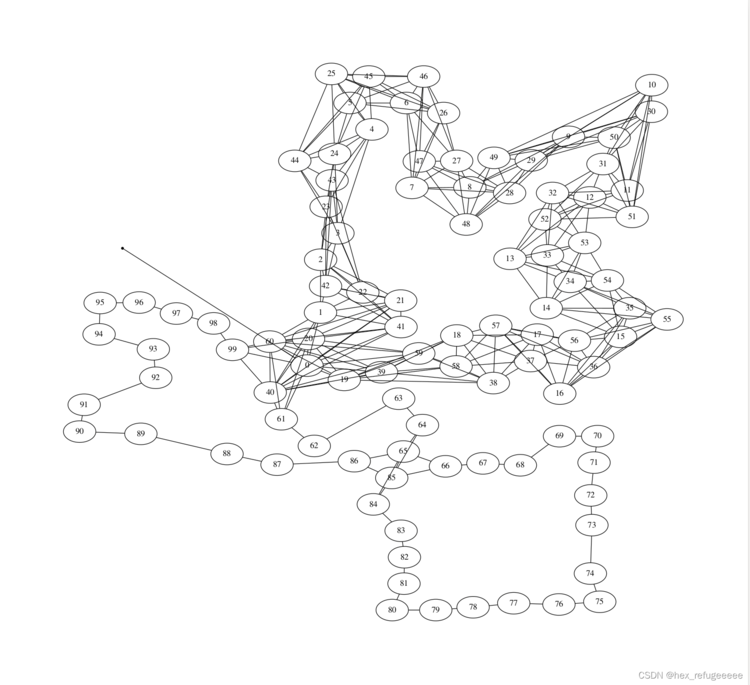
七、Pose2SLAMStressTest.cpp
std::random_device rd;
std::mt19937 e2(rd());
std::uniform_real_distribution<> dist(0, 1);
vector
for (int i &#61; 0; i
double r &#61; dist(e2);
r &#61; (r - 0.5) / 10 &#43; i;
M <<1, 0, 0, r, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1;
poses.push_back(Pose3(M));
}
八、Pose2SLAMwSPCG.cpp // 4. Single Step Optimization using Levenberg-Marquardt
LevenbergMarquardtParams parameters;
parameters.verbosity &#61; NonlinearOptimizerParams::ERROR;
parameters.verbosityLM &#61; LevenbergMarquardtParams::LAMBDA;
// LM is still the outer optimization loop, but by specifying "Iterative" below
// We indicate that an iterative linear solver should be used.
// In addition, the *type* of the iterativeParams decides on the type of
// iterative solver, in this case the SPCG (subgraph PCG)
parameters.linearSolverType &#61; NonlinearOptimizerParams::Iterative;
parameters.iterativeParams &#61; boost::make_shared

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有