一 介绍
为何要有索引?
一般的应用系统,读写比例在10:1左右,而且插入操作和一般的更新操作很少出现性能问题,在生产环境中,我们遇到最多的,也是最容易出问题的,还是一些复杂的查询操作,因此对查询语句的优化显然是重中之重。说起加速查询,就不得不提到索引了。
什么是索引?
索引在MySQL中也叫做“键”,是存储引擎用于快速找到记录的一种数据结构。索引对于良好的性能
非常关键,尤其是当表中的数据量越来越大时,索引对于性能的影响愈发重要。
索引优化应该是对查询性能优化最有效的手段了。索引能够轻易将查询性能提高好几个数量级。
索引相当于字典的音序表,如果要查某个字,如果不使用音序表,则需要从几百页中逐页去查。
3010 405 15 35 661 6 11 19 21 39 55 100
你是否对索引存在误解?
索引是应用程序设计和开发的一个重要方面。若索引太多,应用程序的性能可能会受到影响。而索引太少,对查询性能又会产生影响,要找到一个平衡点,这对应用程序的性能至关重要。一些开发人员总是在事后才想起添加索引----我一直认为,这源于一种错误的开发模式。如果知道数据的使用,从一开始就应该在需要处添加索引。开发人员往往对数据库的使用停留在应用的层面,比如编写SQL语句、存储过程之类,他们甚至可能不知道索引的存在,或认为事后让相关DBA加上即可。DBA往往不够了解业务的数据流,而添加索引需要通过监控大量的SQL语句进而从中找到问题,这个步骤所需的时间肯定是远大于初始添加索引所需的时间,并且可能会遗漏一部分的索引。当然索引也并不是越多越好,我曾经遇到过这样一个问题:某台MySQL服务器iostat显示磁盘使用率一直处于100%,经过分析后发现是由于开发人员添加了太多的索引,在删除一些不必要的索引之后,磁盘使用率马上下降为20%。可见索引的添加也是非常有技术含量的。
二 索引的原理
一 索引原理
索引的目的在于提高查询效率,与我们查阅图书所用的目录是一个道理:先定位到章,然后定位到该章下的一个小节,然后找到页数。相似的例子还有:查字典,查火车车次,飞机航班等
本质都是:通过不断地缩小想要获取数据的范围来筛选出最终想要的结果,同时把随机的事件变成顺序的事件,也就是说,有了这种索引机制,我们可以总是用同一种查找方式来锁定数据。
数据库也是一样&#xff0c;但显然要复杂的多&#xff0c;因为不仅面临着等值查询&#xff0c;还有范围查询(>、<、between、in)、模糊查询(like)、并集查询(or)等等。数据库应该选择怎么样的方式来应对所有的问题呢&#xff1f;我们回想字典的例子&#xff0c;能不能把数据分成段&#xff0c;然后分段查询呢&#xff1f;最简单的如果1000条数据&#xff0c;1到100分成第一段&#xff0c;101到200分成第二段&#xff0c;201到300分成第三段......这样查第250条数据&#xff0c;只要找第三段就可以了&#xff0c;一下子去除了90%的无效数据。但如果是1千万的记录呢&#xff0c;分成几段比较好&#xff1f;稍有算法基础的同学会想到搜索树&#xff0c;其平均复杂度是lgN&#xff0c;具有不错的查询性能。但这里我们忽略了一个关键的问题&#xff0c;复杂度模型是基于每次相同的操作成本来考虑的。而数据库实现比较复杂&#xff0c;一方面数据是保存在磁盘上的&#xff0c;另外一方面为了提高性能&#xff0c;每次又可以把部分数据读入内存来计算&#xff0c;因为我们知道访问磁盘的成本大概是访问内存的十万倍左右&#xff0c;所以简单的搜索树难以满足复杂的应用场景。
二 磁盘IO与预读
前面提到了访问磁盘&#xff0c;那么这里先简单介绍一下磁盘IO和预读&#xff0c;磁盘读取数据靠的是机械运动&#xff0c;每次读取数据花费的时间可以分为寻道时间、旋转延迟、传输时间三个部分&#xff0c;寻道时间指的是磁臂移动到指定磁道所需要的时间&#xff0c;主流磁盘一般在5ms以下&#xff1b;旋转延迟就是我们经常听说的磁盘转速&#xff0c;比如一个磁盘7200转&#xff0c;表示每分钟能转7200次&#xff0c;也就是说1秒钟能转120次&#xff0c;旋转延迟就是1/120/2 &#61; 4.17ms&#xff1b;传输时间指的是从磁盘读出或将数据写入磁盘的时间&#xff0c;一般在零点几毫秒&#xff0c;相对于前两个时间可以忽略不计。那么访问一次磁盘的时间&#xff0c;即一次磁盘IO的时间约等于5&#43;4.17 &#61; 9ms左右&#xff0c;听起来还挺不错的&#xff0c;但要知道一台500 -MIPS&#xff08;Million Instructions Per Second&#xff09;的机器每秒可以执行5亿条指令&#xff0c;因为指令依靠的是电的性质&#xff0c;换句话说执行一次IO的时间可以执行约450万条指令&#xff0c;数据库动辄十万百万乃至千万级数据&#xff0c;每次9毫秒的时间&#xff0c;显然是个灾难。下图是计算机硬件延迟的对比图&#xff0c;供大家参考&#xff1a;

考虑到磁盘IO是非常高昂的操作&#xff0c;计算机操作系统做了一些优化&#xff0c;当一次IO时&#xff0c;不光把当前磁盘地址的数据&#xff0c;而是把相邻的数据也都读取到内存缓冲区内&#xff0c;因为局部预读性原理告诉我们&#xff0c;当计算机访问一个地址的数据的时候&#xff0c;与其相邻的数据也会很快被访问到。每一次IO读取的数据我们称之为一页(page)。具体一页有多大数据跟操作系统有关&#xff0c;一般为4k或8k&#xff0c;也就是我们读取一页内的数据时候&#xff0c;实际上才发生了一次IO&#xff0c;这个理论对于索引的数据结构设计非常有帮助。
三 索引的数据结构
前面讲了索引的基本原理&#xff0c;数据库的复杂性&#xff0c;又讲了操作系统的相关知识&#xff0c;目的就是让大家了解&#xff0c;任何一种数据结构都不是凭空产生的&#xff0c;一定会有它的背景和使用场景&#xff0c;我们现在总结一下&#xff0c;我们需要这种数据结构能够做些什么&#xff0c;其实很简单&#xff0c;那就是&#xff1a;每次查找数据时把磁盘IO次数控制在一个很小的数量级&#xff0c;最好是常数数量级。那么我们就想到如果一个高度可控的多路搜索树是否能满足需求呢&#xff1f;就这样&#xff0c;b&#43;树应运而生&#xff08;B&#43;树是通过二叉查找树&#xff0c;再由平衡二叉树&#xff0c;B树演化而来&#xff09;。
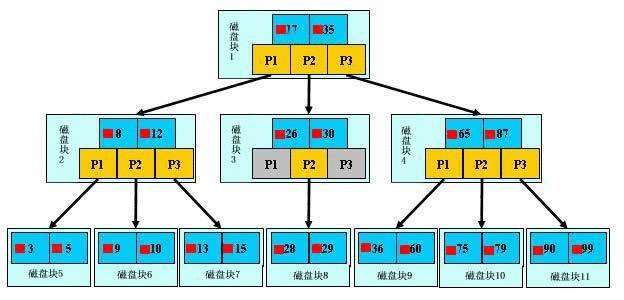
如上图&#xff0c;是一颗b&#43;树&#xff0c;关于b&#43;树的定义可以参见B&#43;树&#xff0c;这里只说一些重点&#xff0c;浅蓝色的块我们称之为一个磁盘块&#xff0c;可以看到每个磁盘块包含几个数据项&#xff08;深蓝色所示&#xff09;和指针&#xff08;黄色所示&#xff09;&#xff0c;如磁盘块1包含数据项17和35&#xff0c;包含指针P1、P2、P3&#xff0c;P1表示小于17的磁盘块&#xff0c;P2表示在17和35之间的磁盘块&#xff0c;P3表示大于35的磁盘块。真实的数据存在于叶子节点即3、5、9、10、13、15、28、29、36、60、75、79、90、99。非叶子节点只不存储真实的数据&#xff0c;只存储指引搜索方向的数据项&#xff0c;如17、35并不真实存在于数据表中。
###b&#43;树的查找过程
如图所示&#xff0c;如果要查找数据项29&#xff0c;那么首先会把磁盘块1由磁盘加载到内存&#xff0c;此时发生一次IO&#xff0c;在内存中用二分查找确定29在17和35之间&#xff0c;锁定磁盘块1的P2指针&#xff0c;内存时间因为非常短&#xff08;相比磁盘的IO&#xff09;可以忽略不计&#xff0c;通过磁盘块1的P2指针的磁盘地址把磁盘块3由磁盘加载到内存&#xff0c;发生第二次IO&#xff0c;29在26和30之间&#xff0c;锁定磁盘块3的P2指针&#xff0c;通过指针加载磁盘块8到内存&#xff0c;发生第三次IO&#xff0c;同时内存中做二分查找找到29&#xff0c;结束查询&#xff0c;总计三次IO。真实的情况是&#xff0c;3层的b&#43;树可以表示上百万的数据&#xff0c;如果上百万的数据查找只需要三次IO&#xff0c;性能提高将是巨大的&#xff0c;如果没有索引&#xff0c;每个数据项都要发生一次IO&#xff0c;那么总共需要百万次的IO&#xff0c;显然成本非常非常高。
###b&#43;树性质
1.索引字段要尽量的小&#xff1a;通过上面的分析&#xff0c;我们知道IO次数取决于b&#43;数的高度h&#xff0c;假设当前数据表的数据为N&#xff0c;每个磁盘块的数据项的数量是m&#xff0c;则有h&#61;㏒(m&#43;1)N&#xff0c;当数据量N一定的情况下&#xff0c;m越大&#xff0c;h越小&#xff1b;而m &#61; 磁盘块的大小 / 数据项的大小&#xff0c;磁盘块的大小也就是一个数据页的大小&#xff0c;是固定的&#xff0c;如果数据项占的空间越小&#xff0c;数据项的数量越多&#xff0c;树的高度越低。这就是为什么每个数据项&#xff0c;即索引字段要尽量的小&#xff0c;比如int占4字节&#xff0c;要比bigint8字节少一半。这也是为什么b&#43;树要求把真实的数据放到叶子节点而不是内层节点&#xff0c;一旦放到内层节点&#xff0c;磁盘块的数据项会大幅度下降&#xff0c;导致树增高。当数据项等于1时将会退化成线性表。
2.索引的最左匹配特性&#xff1a;当b&#43;树的数据项是复合的数据结构&#xff0c;比如(name,age,sex)的时候&#xff0c;b&#43;数是按照从左到右的顺序来建立搜索树的&#xff0c;比如当(张三,20,F)这样的数据来检索的时候&#xff0c;b&#43;树会优先比较name来确定下一步的所搜方向&#xff0c;如果name相同再依次比较age和sex&#xff0c;最后得到检索的数据&#xff1b;但当(20,F)这样的没有name的数据来的时候&#xff0c;b&#43;树就不知道下一步该查哪个节点&#xff0c;因为建立搜索树的时候name就是第一个比较因子&#xff0c;必须要先根据name来搜索才能知道下一步去哪里查询。比如当(张三,F)这样的数据来检索时&#xff0c;b&#43;树可以用name来指定搜索方向&#xff0c;但下一个字段age的缺失&#xff0c;所以只能把名字等于张三的数据都找到&#xff0c;然后再匹配性别是F的数据了&#xff0c; 这个是非常重要的性质&#xff0c;即索引的最左匹配特性。
四 聚集索引与辅助索引
在数据库中&#xff0c;B&#43;树的高度一般都在2~4层&#xff0c;这也就是说查找某一个键值的行记录时最多只需要2到4次IO&#xff0c;这倒不错。因为当前一般的机械硬盘每秒至少可以做100次IO&#xff0c;2~4次的IO意味着查询时间只需要0.02~0.04秒。
数据库中的B&#43;树索引可以分为聚集索引&#xff08;clustered index&#xff09;和辅助索引&#xff08;secondary index&#xff09;&#xff0c;
聚集索引与辅助索引相同的是&#xff1a;不管是聚集索引还是辅助索引&#xff0c;其内部都是B&#43;树的形式&#xff0c;即高度是平衡的&#xff0c;叶子结点存放着所有的数据。
聚集索引与辅助索引不同的是&#xff1a;叶子结点存放的是否是一整行的信息
1、聚集索引
#InnoDB存储引擎表示索引组织表&#xff0c;即表中数据按照主键顺序存放。而聚集索引&#xff08;clustered index&#xff09;就是按照每张表的主键构造一棵B&#43;树&#xff0c;
同时叶子结点存放的即为整张表的行记录数据&#xff0c;也将聚集索引的叶子结点称为数据页。聚集索引的这个特性决定了索引组织表中数据也是索引的一部分。
同B&#43;树数据结构一样&#xff0c;每个数据页都通过一个双向链表来进行链接。#如果未定义主键&#xff0c;MySQL取第一个唯一索引&#xff08;unique&#xff09;而且只含非空列&#xff08;NOT NULL&#xff09;作为主键&#xff0c;InnoDB使用它作为聚簇索引。#如果没有这样的列&#xff0c;InnoDB就自己产生一个这样的ID值&#xff0c;它有六个字节&#xff0c;而且是隐藏的&#xff0c;使其作为聚簇索引。#由于实际的数据页只能按照一棵B&#43;树进行排序&#xff0c;因此每张表只能拥有一个聚集索引。在多少情况下&#xff0c;查询优化器倾向于采用聚集索引。
因为聚集索引能够在B&#43;树索引的叶子节点上直接找到数据。此外由于定义了数据的逻辑顺序&#xff0c;聚集索引能够特别快地访问针对范围值得查询。
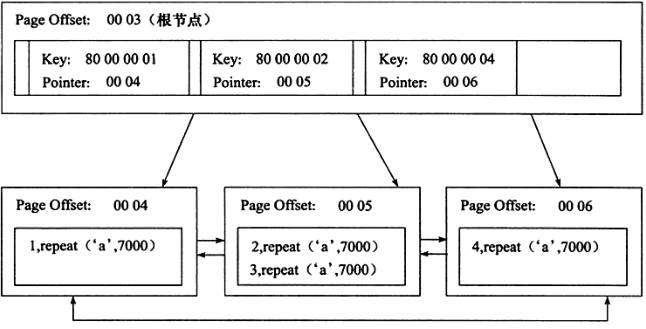
聚集索引的好处之一&#xff1a;它对主键的排序查找和范围查找速度非常快&#xff0c;叶子节点的数据就是用户所要查询的数据。如用户需要查找一张表&#xff0c;查询最后的10位用户信息&#xff0c;由于B&#43;树索引是双向链表&#xff0c;所以用户可以快速找到最后一个数据页&#xff0c;并取出10条记录
#参照第六小结测试索引的准备阶段来创建出表s1
mysql> desc s1; #最开始没有主键
&#43;--------&#43;-------------&#43;------&#43;-----&#43;---------&#43;-------&#43;
| Field | Type | Null | Key | Default | Extra |
&#43;--------&#43;-------------&#43;------&#43;-----&#43;---------&#43;-------&#43;
| id | int(11) | NO | | NULL | |
| name | varchar(20) | YES | | NULL | |
| gender | char(6) | YES | | NULL | |
| email | varchar(50) | YES | | NULL | |
&#43;--------&#43;-------------&#43;------&#43;-----&#43;---------&#43;-------&#43;
4 rows in set (0.00 sec)mysql> explain select * from s1 order by id desc limit 10; #Using filesort&#xff0c;需要二次排序
&#43;----&#43;-------------&#43;-------&#43;------------&#43;------&#43;---------------&#43;------&#43;---------&#43;------&#43;---------&#43;----------&#43;----------------&#43;
| id | select_type | table | partitions | type | possible_keys | key | key_len | ref | rows | filtered | Extra |
&#43;----&#43;-------------&#43;-------&#43;------------&#43;------&#43;---------------&#43;------&#43;---------&#43;------&#43;---------&#43;----------&#43;----------------&#43;
| 1 | SIMPLE | s1 | NULL | ALL | NULL | NULL | NULL | NULL | 2633472 | 100.00 | Using filesort |
&#43;----&#43;-------------&#43;-------&#43;------------&#43;------&#43;---------------&#43;------&#43;---------&#43;------&#43;---------&#43;----------&#43;----------------&#43;
1 row in set, 1 warning (0.11 sec)mysql> alter table s1 add primary key(id); #添加主键
Query OK, 0 rows affected (13.37 sec)
Records: 0 Duplicates: 0 Warnings: 0mysql> explain select * from s1 order by id desc limit 10; #基于主键的聚集索引在创建完毕后就已经完成了排序&#xff0c;无需二次排序
&#43;----&#43;-------------&#43;-------&#43;------------&#43;-------&#43;---------------&#43;---------&#43;---------&#43;------&#43;------&#43;----------&#43;-------&#43;
| id | select_type | table | partitions | type | possible_keys | key | key_len | ref | rows | filtered | Extra |
&#43;----&#43;-------------&#43;-------&#43;------------&#43;-------&#43;---------------&#43;---------&#43;---------&#43;------&#43;------&#43;----------&#43;-------&#43;
| 1 | SIMPLE | s1 | NULL | index | NULL | PRIMARY | 4 | NULL | 10 | 100.00 | NULL |
&#43;----&#43;-------------&#43;-------&#43;------------&#43;-------&#43;---------------&#43;---------&#43;---------&#43;------&#43;------&#43;----------&#43;-------&#43;
1 row in set, 1 warning (0.04 sec)
聚集索引的好处之二&#xff1a;范围查询&#xff08;range query&#xff09;&#xff0c;即如果要查找主键某一范围内的数据&#xff0c;通过叶子节点的上层中间节点就可以得到页的范围&#xff0c;之后直接读取数据页即可






 京公网安备 11010802041100号
京公网安备 11010802041100号