adaboost深入剖析（上）

真的是太久不写博客了&＃xff0c;两个原因&＃xff0c;一是懒&＃xff0c;二是机器学习这个领域真的是浩如烟海&＃xff0c;我要学的东西太多了&＃xff0c;不知道该从何说起&＃xff0c;但是又总会有某个瞬间&＃xff0c;感觉自己如获至宝&＃xff0c;学到了某些很奇妙的东西&＃xff0c;就会有一种想要立刻把它给写下来的冲动。今天这一篇主要想给大家介绍一下adaboost这个算法&＃xff0c;前几天听了向世明老师的课&＃xff0c;自己课下又推了几遍&＃xff0c;简直神奇。

一&＃xff09;基础知识

可能有的朋友刚刚接触这个领域&＃xff0c;为了方便大家都能看得懂&＃xff0c;我先说一些基础知识。假如有一组数据&＃xff0c;分布在一维平面上&＃xff0c;数据和标签如下图所示&＃xff1a;

那么大家一看就知到这不是一个简单的线性可分的问题&＃xff0c;为了跟直观的给大家感受&＃xff0c;做个这样的图

那么什么分类器&＃xff0c;你给我画一条线&＃xff0c;把这些点分为左边和右边。

什么叫线性可分&＃xff0c;通过你构建一个分类器&＃xff0c;能够完整的把这些点给分开&＃xff0c;左边全是红圈&＃xff0c;右边都是篮框&＃xff0c;这叫线性可分

那么什么叫线性不可分&＃xff0c;上图所示就是线性不可分&＃xff0c;你通过一条线分不开

在给大家介绍两个概念&＃xff0c;什么叫弱分类器&＃xff0c;就是通过你画的一条线&＃xff0c;虽然不能完全画分&＃xff0c;但是准确率是比随机猜测要好的&＃xff0c;比如我以x&＃61;3.5作为分类器&＃xff0c;准确率为0.7&＃xff0c;要大于随机猜测的0.5&＃xff0c;但是效果又不是很好&＃xff0c;所以我们叫它弱分类器。

那么什么叫做强分类器呢&＃xff0c;我构建的这个分类器的正确率很高&＃xff0c;所以叫强分类器。

那么很明显&＃xff0c;本题所举的例子中&＃xff0c;通过直接在一维空间没有办法构造出强分类器&＃xff0c;那么怎么办呢&＃xff1f;

有人就提出了&＃xff0c;弱可学习问题能否向强可学习问题转化

1990年&＃xff0c; Schapire通过一个构造性方法对“等价性” 问题作出了肯定的回答。 证明多个弱分类器可以集成为一个强分类器。 这就形成了集成学习的理论基础。

我们今天介绍的adaboost算法就是一种经典的集成学习的方法。

二&＃xff09;adaboost算法介绍

adaboost算法可以用这么一句话简单概括&＃xff1a;从弱学习算法出发&＃xff0c; 反复学习&＃xff0c; 得到一系列弱分类器&＃xff1b;然后组合这些弱分类器&＃xff0c; 构成一个强分类器。具体方法是&＃xff1a;提高那些被前一轮弱分类器分错的样本的权重&＃xff0c; 降低已经被正确分类的样本的权重。 错分的样本将在下一轮弱分类器中得到更多关注。

1&＃xff09;训练数据集

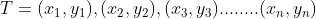
其中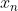代表第n个数据点的数据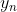&＃xff0c;代表第i个的标签&＃xff0c;值为1或-1.

弱学习算法

2&＃xff09;会给每个数据一开始都分配一个权重&＃xff0c;一开始这个权重是相等的都是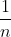,等到一个弱训练器训练结束之后&＃xff0c;会对分对的数据减小权重&＃xff0c;对分错的数据增大权重&＃xff0c;也就是说在下一个弱分类器中将注意力更多的关注到被错分的数据中去。

权重表示为:,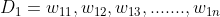

权重初始化为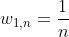

3&＃xff09;循环&＃xff1a;m&＃61;1,2,3......n:

训练第m个弱分类器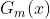&＃xff1a;,输出结果为1或者-1&＃xff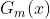0c;

4&＃xff09;计算在数据集上的分类错误率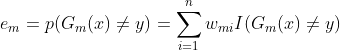&＃xff1a;

这里需要提醒一点&＃xff0c;这个错误率不能高于0.5&＃xff0c;不然瞎猜都比你分类器正确率高&＃xff0c;要你何用&＃xff1f;嗯&＃xff0c;学术点讲是&＃xff0c;不然这个所分类器就没有办法对最后的集成学习带来正面效果。

5&＃xf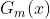f09;计算在最终集成分类器中的贡献系数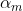&＃xff0c;我们所有的弱分类器最终都是要通过加权集成算法来合并为一个强分类器&＃xff0c;所以这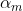个贡献系数就显得特别重要

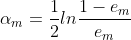
从公式可以得知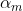将随着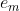的减小而增大。也就是说分类错误率越低的分类器最终对于集成分类器的贡献是越大的

6&＃xff09;从更新各数据点权重&＃xff0c;这一步是很关键的一步&＃xff0c;也可以说是整个adaboost算法的灵魂。

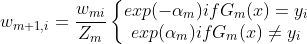
可以观察到这个式子中上下只差了一个负号&＃xff0c;就是说如果预测结果与真实标签相同则是正号&＃xff0c;如果不同就是负号。则上述公式可以改写为&＃xff1a;

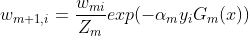
同时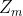是个归一化因子&＃xff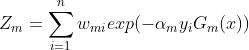0c;可写为

对4,5,6三步进行循环

7&＃xff09;构建弱分类器的线性组合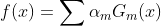

最后一句话如果不讲&＃xff0c;很多朋友可能会掉坑里&＃xff0c;对于最后的分类器我们需要在加一个符号函数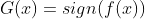,因为如果是一个二分类问题&＃xff0c;则我们简单的通过区别正负号就可以获得两类的标签&＃xff0c;所以加个符号函数实际上就是从输出到最终标签的转化过程。

三&＃xff09;看一个例子

巴拉巴拉讲半天&＃xff0c;不上点干货朋友们可能还是有点蒙蔽&＃xff0c;就拿第一部分举的一维分类的例子来讲好了&＃xff1a;

初始化权重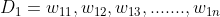都为0.1

m&＃61;1第一个分类器训练过程

在权值分布为 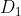的训练数据上&＃xff0c;阈值 v 取2.5时分类误差率最低 (取不同的阈值&＃xff0c;然后计算加权错误率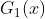&＃xff0c;选择最小者&＃xff0c;故基本分类器 为&＃xff1a;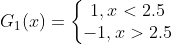

训练误差为&＃xff1a;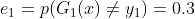

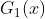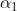计算的系数为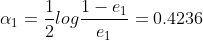

更新训练的权值分布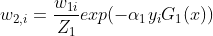得到的值为

分类器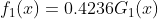,在数据集上的错误率为0.3

m&＃61;2第二个分类器训练过程

在权值分布为 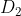的训练数据上&＃xff0c;阈值 v 取8.5时分类误差率最低 (取不同的阈值&＃xff0c;然后计算加权错误率&＃xff0c;选择最小者&＃xff0c;故基本分类器 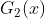为&＃xff1a;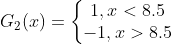

训练误差为&＃xff1a;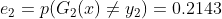

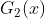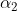计算的系数为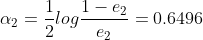

更新训练的权值分布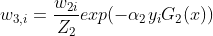得到的值为

分类器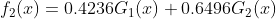,在数据集上的错误率为0.3

m&＃61;3第三个分类器训练过程

在权值分布为 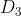的训练数据上&＃xff0c;阈值 v 取5.5时分类误差率最低 (取不同的阈值&＃xff0c;然后计算加权错误率&＃xff0c;选择最小者&＃xff0c;故基本分类器 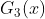为&＃xff1a;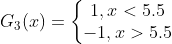

训练误差为&＃xff1a;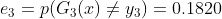

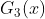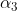计算的系数为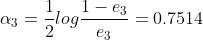

更新训练的权值分布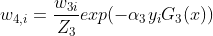得到的值为

分类器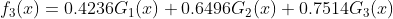,在数据集上的错误率为0

哎&＃xff0c;有没有很惊讶&＃xff0c;仅仅三个弱分类器就组成了一个强分类器&＃xff0c;并且完成了貌似不可能的工作

哈哈哈&＃xff0c;科普部分到这里就结束了&＃xff0c;在下一篇《adaboost深入剖析&＃xff08;下&＃xff09;》中&＃xff0c;我会对为什么adaboost能够有这么好的效果进行理论的证明&＃xff0c;有兴趣的同学可以跟下去。

参考&＃xff1a;

向世明老师课堂所讲以及李航老师《统计学习原理》

个人学习笔记&＃xff0c;欢迎学习交流指正。我是钱多多