文章目录[隐藏]
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
第一行包含两个整数 N,MN,M,表示该图共有 NN 个结点和 MM 条无向边。
接下来 MM 行每行包含三个整数 X_i,Y_i,Z_iXi,Yi,Zi,表示有一条长度为 Z_iZi 的无向边连接结点 X_i,Y_iXi,Yi。
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
输入 #1
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
输出 #1
7
数据规模:
对于 20/%20% 的数据,N/le 5N≤5,M/le 20M≤20。
对于 40/%40% 的数据,N/le 50N≤50,M/le 2500M≤2500。
对于 70/%70% 的数据,N/le 500N≤500,M/le 10^4M≤104。
对于 100/%100% 的数据:1/le N/le 50001≤N≤5000,1/le M/le 2/times 10^51≤M≤2×105,1/le Z_i /le 10^41≤Zi≤104。
样例解释:
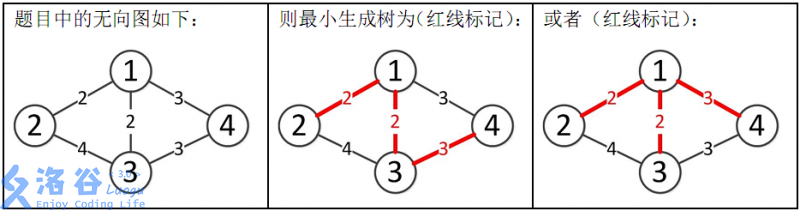
所以最小生成树的总边权为 2+2+3=7。
【解析】
本题是一道板子题
首先先看一下prim算法的思路
最小生成树可以看作一个集合
用样例模拟下过程:
minn:每个节点的最小边权
白点:未进入集合的节点
蓝点:已进入集合的节点
红线:最小生成树的边
1.通过输入可以画出下面的图
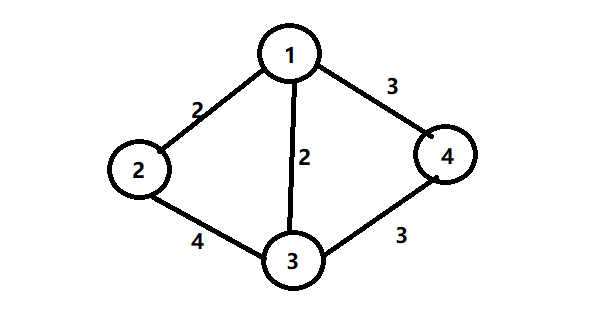
2.将图的各个节点赋初值 minn[1]=0,其余赋值为正无穷
3.找到最小边的点1,并加入生成的树(可以理解为一个集合)
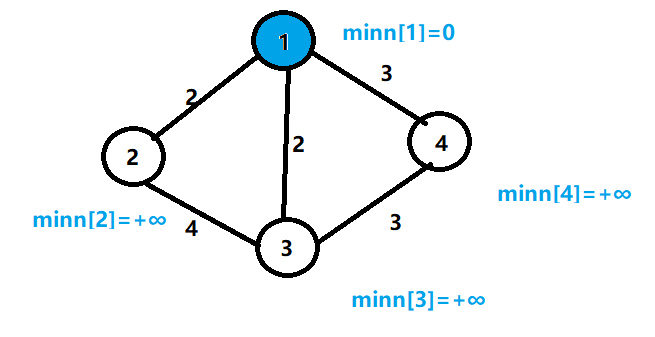
4.更改与节点1相连的节点边权的最小值
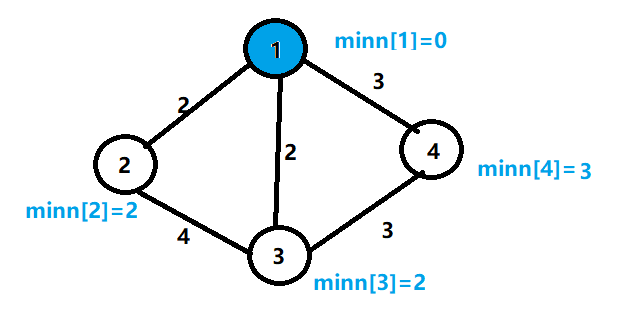
5.找到集合外的最小边的节点2,并加入集合
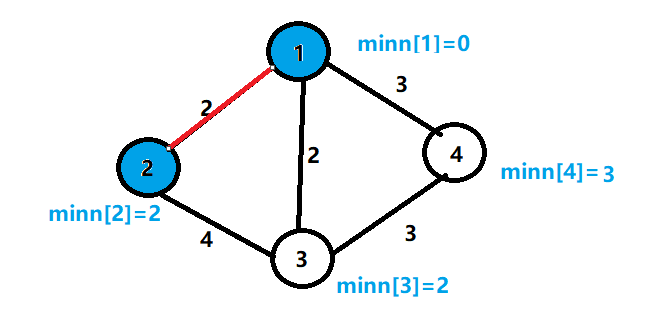
6.更改与节点2相连的节点边权的最小值
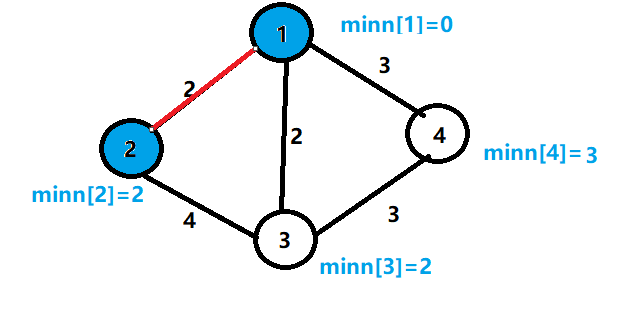
7.找到集合外的最小边的节点3,并加入集合
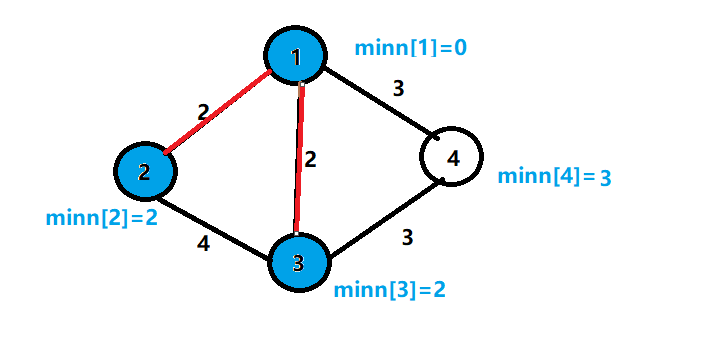
8.更改与节点3相连的节点边权的最小值
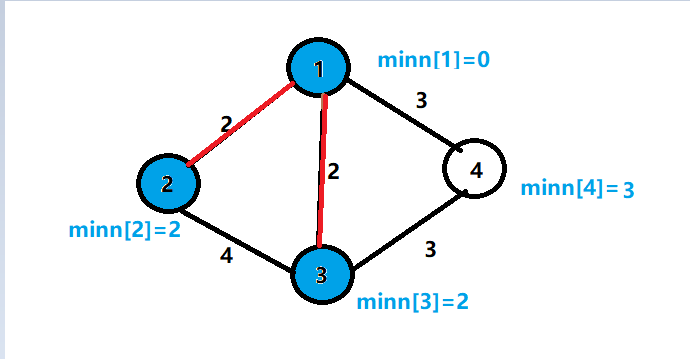
9.找到集合外的最小边的节点4,并加入集合
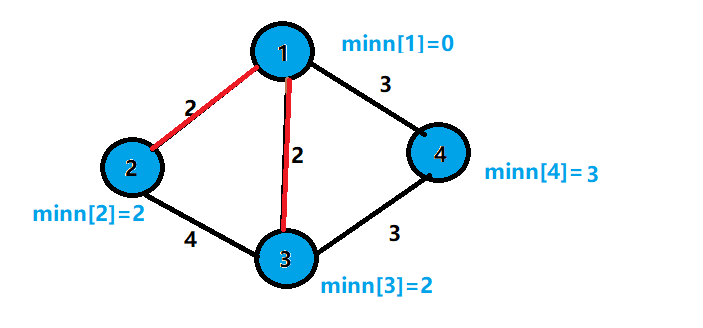
这时候有两种不同的树
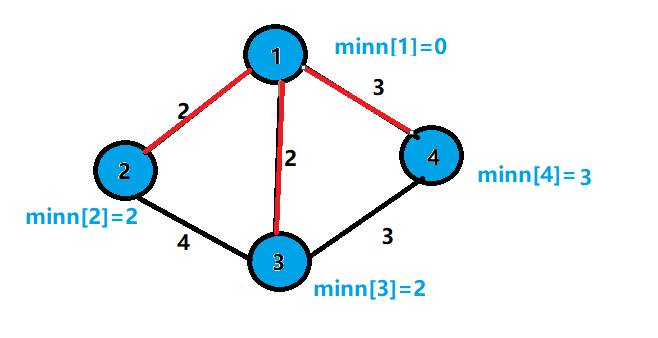
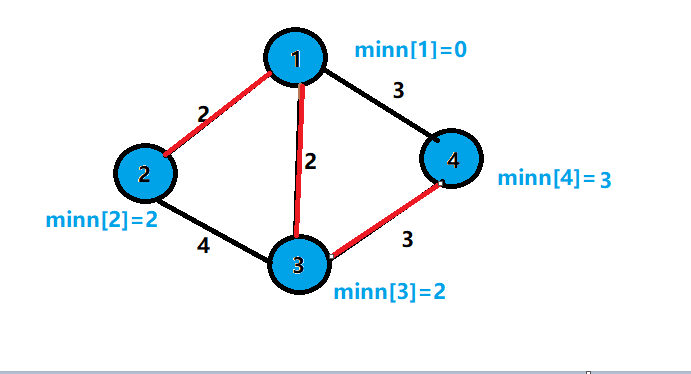
10.更改与节点4相连的节点边权的最小值


上面的步骤整理一下就变成了:
for(遍历每个节点){
找到集合外最小的节点k(与集合有连边)
更改与k相连的节点的最小值
}
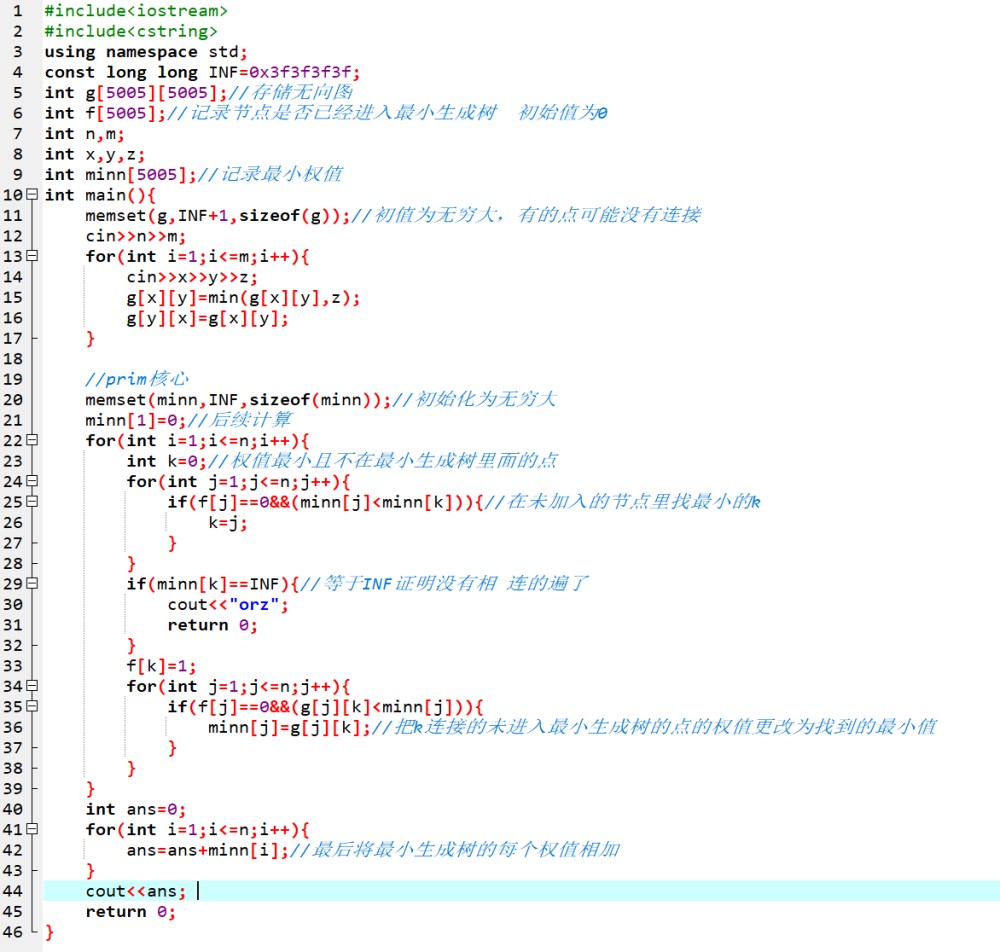
【代码】
这道题还需要注意判断图是否联通,有的边可能重复输入,要取最小的权值

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有