一,算法介绍
在CS124课程的第一周提到 求解两个字符串相似度的算法---Minimum Edit Distance(最短编辑距离)算法。该算法在NLP(自然语言处理)中也会用到。
如何定义相似度呢?任给两个字符串X 和Y,使用以下三种操作将 字符串X 变到 字符串Y :①插入(Insert)操作;②删除操作(delete);③替换操作(substitute)
比如 字符串X="intention" , 字符串Y="execution"。从字符串X 转换成 字符串Y 如下图所示:

定义:插入操作的代价为1,删除操作的代价为1,替换操作的代价为2(称为: Levenshtein distance)。那么,"intention" 变成 "execution" 执行了三次替换,一次删除,一次插入。因此,总代价为8
而这个代价又称为编辑距离, 用之来 衡量 两个字符串的相似程度。显然,若两个字符串越相似,则从一个字符串变到另一个字符串所需要的 “操作” 步骤 就越少。
二,动态规则求解最短编辑距离
为什么能用动态规划来求解呢??该问题可以分解成若干个子问题;?子问题之间具有重叠性(可“查表”),具体可参考一些动态规划的示例1,示例2.
假设字符串X的长度为n,字符串Y的长度为m,用d[n][m] 表示 字符串X 转换成 字符串Y 的最短编辑距离
定义 d[i][j] 表示 字符串X的子串X[1...i] 转换成 字符串Y 的子串 Y[1...j] 的最短编辑距离(这里的 下标从1开始,不从0开始),有如下动态规划公式:
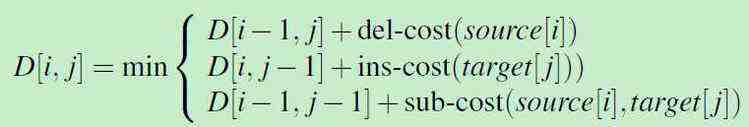
要想从 长度为 i 的源字符串X 转换成 长度为 j 的目标字符串Y,有三种方式:
①先将 源字符串X 的前 i-1 个字符 X[1...i-1] 转换成 目标字符串Y[1...j], 然后再 删除字符串X 的第 i 个字符source[i]
②先将 源字符串X[1...j] 转换成 目标字符串Y[1...j-1] ,然后再 插入字符串Y的第 j 个字符 target[j]
③先将 源字符串X[1...i-1] 转换成 目标字符串Y[1...j-1],然后 源字符串中的 第 i 个字符X[i] 替换为 目标字符串的第 j 个字符 Y[j]
为什么 只有上述三种方式呢?
因为我们是将 源问题 的求解,分解成若干个子问题的求解,子问题的规模比原问题要小1。源问题 X[1...i] 转换成 Y[1...j] 。比如,子问题是:先将X[1...i-1] 转换成 Y[1...j] ,...
结合前面定义的 操作代价(删除和插入操作代价为1,替换操作为2),就是下面这个公式:
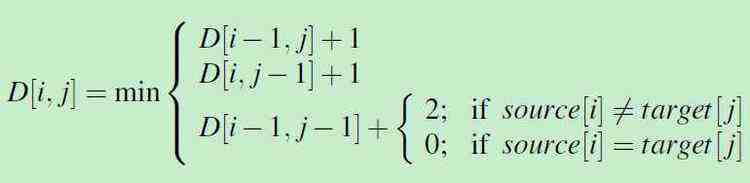
解释一下为什么 if source[i]=target[j]时,替换的 代价为0呢?if source[i]=target[j] 表明 字符串X 的第 i 个字符串 和 字符串Y的第 j 个字符是相同的
要想将 X[1...i] 转换成 Y[1...j] ,对于第三种转换方式:先将 源字符串X[1...i-1] 转换成 目标字符串Y[1...j-1] ,既然:字符串X 的第 i 个字符串 和 字符串Y的第 j 个字符是相同的,那就相当于“自己替换自己”,或者说是 不需要替换操作了嘛。这也是下面代码实现逻辑:
if (source.charAt(i-1) == target.charAt(j-1)) {
dp[i][j] = dp[i - 1][j - 1];
三,代码实现
伪代码描述如下:

JAVA实现:
1 public class MinimumEditDistance {
2
3 public static void main(String[] args) {
4 MinimumEditDistance med = new MinimumEditDistance();
5 String source = "execution";
6 String target = "intention";
7 int result = med.similarDegree(source, target);
8 System.out.println(result);
9 }
10
11 public int similarDegree(String source, String target) {
12 if(source == null || target == null)
13 throw new IllegalArgumentException("illegal input String");
14
15 int sourceLen = source.length();
16 int targetLen = target.length();
17
18 int[][] dp = new int[sourceLen + 1][targetLen +1];
19 //init
20 dp[0][0] = 0;
21 for(int i = 1; i <= sourceLen; i++)
22 dp[i][0] = i;
23 for(int i = 1; i <= targetLen; i++)
24 dp[0][i] = i;
25
26 for(int i = 1; i <= sourceLen; i++) {
27 for(int j = 1; j <= targetLen; j++) {
28 if (source.charAt(i-1) == target.charAt(j-1)) {
29 dp[i][j] = dp[i - 1][j - 1];
30 }else{
31 int insert = dp[i][j - 1] + 1;//source[0,i] to target[0,j-1] then insert target[j]
32 int delete = dp[i - 1][j] + 1;//source[0,i-1] to target[0,j] then delete source[i]
33 int substitute = dp[i - 1][j - 1] + 2;//source[0,i-1] to target[0,j-1] then substitute(source[i] by target[j])
34
35 int min = min(insert, delete, substitute);
36 dp[i][j] = min;
37 }
38 }
39 }
40 return dp[sourceLen][targetLen];
41 }
42
43 private int min(int insert, int delete, int substitute) {
44 int tmp = insert insert:delete;
45 int min = tmp tmp:substitute;
46 return min;
47 }
48 }
参考:Stanford CS124课程
原文:http://www.cnblogs.com/hapjin/p/7467035.html
最短编辑距离算法实现