自举电路可以增加输入阻抗，你知道吗

原文来自公众号：工程师看海

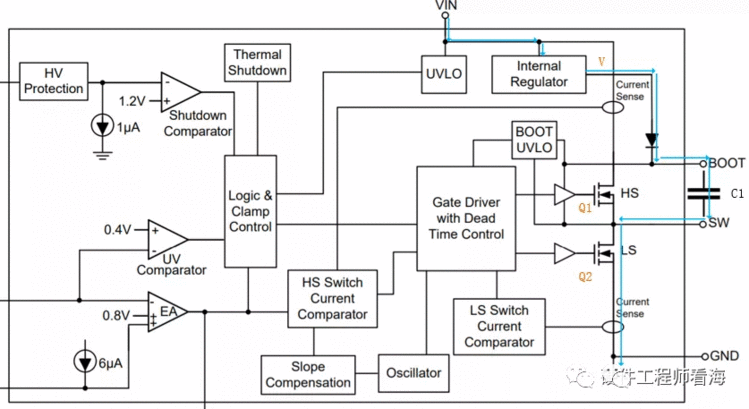
以前写过一篇文章，介绍自举电路在BUCK电源的应用，驱动高边MOS

https://www.dianyuan.com/eestar/article-2127.html

反馈不错，今天再来介绍下自举电路增加输入阻抗的原理，喜欢的同学记得点赞、转发，多多支持！

加微信：chunhou0820

获取自举电路仿真文件

1 输入阻抗的计算方法

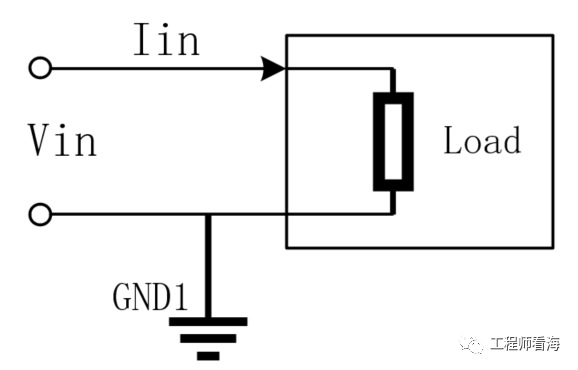
我们从最简单的电路开始一点一点分析，先定义一下输入阻抗的计算过程。我们可以粗略的把负载作为一个黑盒子来对待，所谓的输入阻抗，就是计算输入到这个黑盒子的电压与电流的比值，比如下图，输入阻抗R=Vin/Iin。

2 从最简单的射极跟随器说起

下图是一个射极跟随器，就是输出Vo=Vin（暂时不考虑三极管B极和E极之间的压降）。

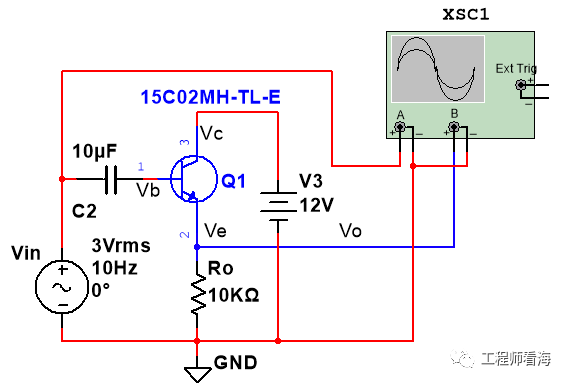
那么它的输入阻抗是多少呢？

假设基极B有一个变换量△Vb，则在发射极E也有一个相应的变换量△Ve，而且二者接近相等，即

△Vb=△Ve

发射极电流的变化量是，

△Ie = △Vb/Ro,

三极管放大倍数为β，则基极B电流变化量

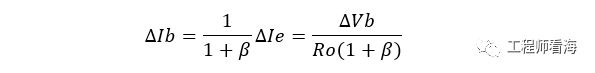
备注：Ie = Ib + Ic = Ib + βIb=（1+β）Ib

输入阻抗为：

三极管放大倍数β很大，一般取100，所以Rin很大，这是它的优点，我们都希望输入阻抗大一些。

其实，我们可以简化分析过程，对于跟随器，Vin=Vb=Ve，则流过基极B的电流变化为

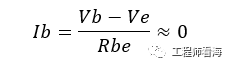
电流很小，因此其阻抗是很大的，这个分析思路后面还会借鉴。

然而这个射极跟随器它有一个巨大的缺点，该电路没有偏执，输出会有失真。

我们看下他的输入和输出波形，红色是输入，蓝色是输出，蓝色峰值电压略低于红色输入，这主要是三极管BE之间的压降引起的，我们不考虑这个压差。最大问题是蓝色没有负电压，只有半波，失真了，没有起到跟随器的作用，因此，我们引入了分压式放大电路，来解决这个失真问题。

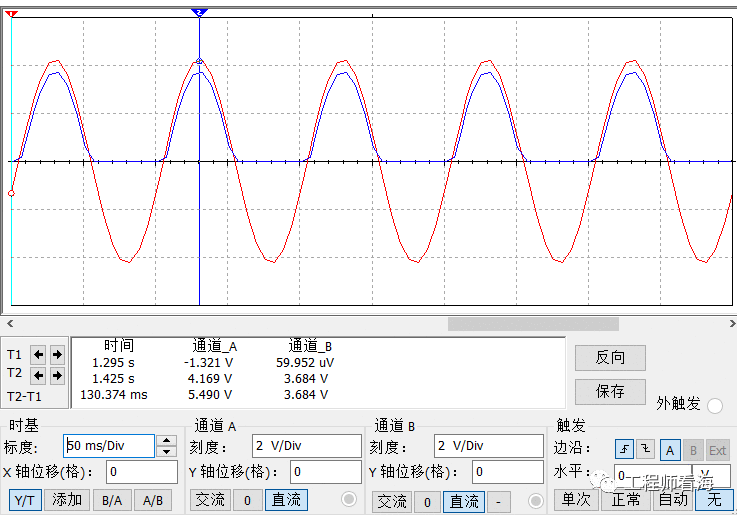
3 分压式共射放大电路

加微信：chunhou0820

获取自举电路仿真文件

分压式共射放大电路全称是分压式负反馈共射放大电路，引入分压式放大电路，提供一个直流偏执后失真就好很多了，R4，R3构成偏执电路，使得输出波形在直流基础之上摆动，避免了负电压失真。

从示波器输出波形可以看到，输出基本跟随输入，只有一点相位延迟，并没有发生失真。

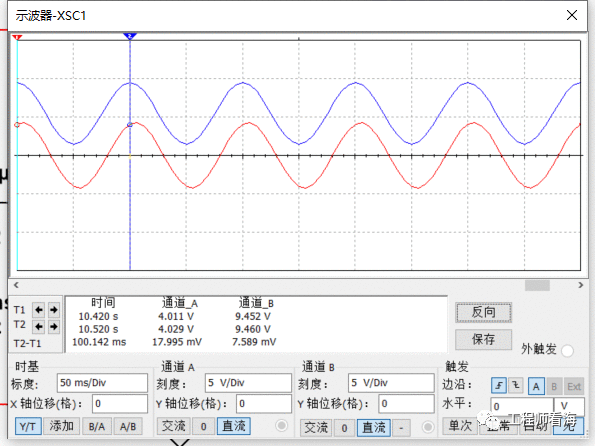
然而这个电路有个稍微不足的地方，那就是输入阻抗低，它的输入阻抗是多少呢？

对于交流信号，交流输入阻抗是R3并R4，大约只有5K，比单纯一个三极管少了不是一点点。这就是他阻抗低的原因，因此可以引入我们今天的主角：

自举电路增加输入阻抗！

铺垫了这么久终于到今天的主角了！

4 分压式共射放大电路与自举电路

这个电路又进化了，有人引入了自举电路。R1与C1构成自举电路，C1的存在使得其对交流通路而言阻抗小很多，可以认为C1两端对于交流而言是短路状态，其结果就导致Vb=Ve，作为射极跟随器使用。

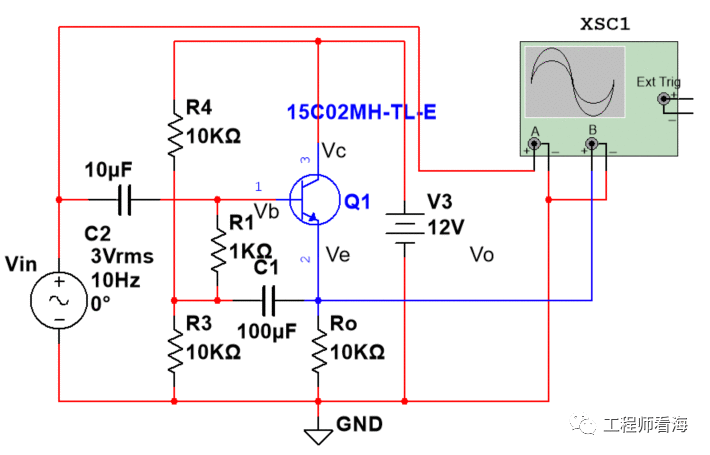
则流过电阻R1的电流：

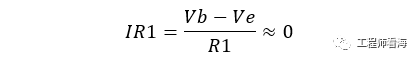
则

因此其输入阻抗是非常大的，这就是自举电路增加输入阻抗的思想。

上面讨论的是分立的三极管，那么对于集成运放又是怎么做的呢？

5 运放与自举电路

对于运放而言，我们就不仿真了，其实原理都是一样的，下图是同向放大，输入阻抗很简单：

R=R4+R5，(比反向放大输入阻抗小很多)

下面是加入自举电路后的同向放大，C1对于交流而言阻抗是非常小的，所以Vc=Vn,

R4两端的电流：

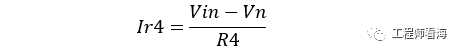
又因为运放的虚短虚断，Vn=Vp=Vin，所以上式变为

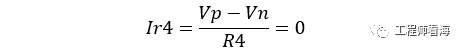
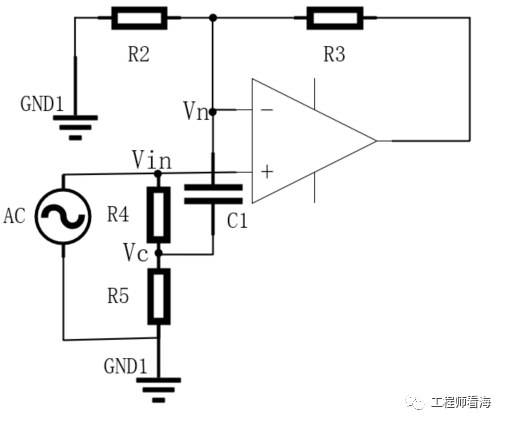
所以流过R4的电流近似为0，其输入阻抗为无穷大，其输入阻抗由普通的同向放大的R4+R5，变为现在的无穷大

Rin=Vin/Ir4=∞

以上就是自举电路增加输入阻抗的分析。

---The end---

限时免费扫码进群，交流更多行业技术

推荐阅读▼

电池、电源

硬件文章精选

华为海思软硬件开发资料

感谢点赞、在看、分享，让知识变得更简单