深入解析KMP算法在字符串匹配中的高效应用

一个主字符串S&＃xff0c;一个模式字符串T&＃xff0c;要求在主字符串中匹配模式字符串&＃xff0c;匹配成功则返回主字符串中和模式字符串匹配成功的第一个字符的位置&＃xff0c;否则返回-1。

字符串匹配简单算法

一个简单的算法思路为&＃xff1a;从主串的第pos个字符起和模式串中的第一个字符比较&＃xff0c;若相等&＃xff0c;则继续比较下一个字符&＃xff1b;若某一个字符不相等&＃xff0c;则从主串的pos&＃43;1个字符起和模式串中的第一个字符再重新比较&＃xff0c;依此类推。若成功则返回第一个字符的位置&＃xff0c;否则返回-1.
代码如下&＃xff1a;

#include
#include
using namespace std;
int index_bf(string S,string T,int pos)
{int i &＃61; pos;int j &＃61; 0;int size_S &＃61; S.size ();int size_T &＃61; T.size ();while(i-j&＃43;size_T <&＃61; size_S && j!&＃61;size_T){if(S[i]&＃61;&＃61;T[j]){i&＃43;&＃43;;j&＃43;&＃43;;}else{i&＃61;i-j&＃43;1;j&＃61;0;}}if(j&＃61;&＃61;size_T)return i-j;elsereturn -1;
}int main()
{string S &＃61; "abcabcabdabba";string T &＃61; "abcabd";int pos &＃61; index_bf(S,T,0);cout<return 0;
}

匹配的过程如下&＃xff1a;
第一轮&＃xff1a;

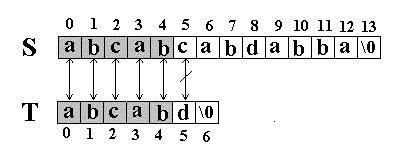
第二轮&＃xff1a;

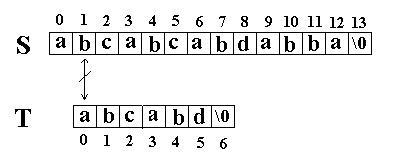
第三轮&＃xff1a;

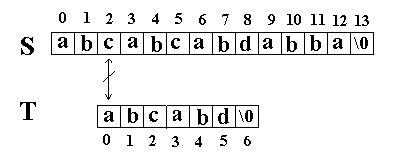
第四轮&＃xff1a;

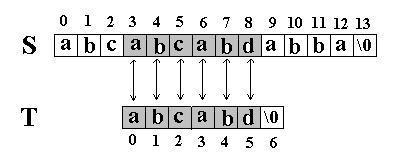
第四轮匹配成功&＃xff0c;函数返回匹配成功的第一个字符的下标&＃xff0c;即3.

在这个算法中&＃xff0c;只要某次匹配不成功&＃xff0c;则T的下标j需要回溯到0&＃xff0c;而S的下标i也回溯同样的距离&＃xff0c;然后S的下标i加1&＃xff0c;从而再次开始匹配。这是一种效率较低的做法&＃xff0c;一种改进的算法是KMP算法。

KMP算法

在KMP算法中&＃xff0c;当某次匹配过程中出现不等时&＃xff0c;不需要回溯指针i&＃xff0c;而是利用已经得到的部分匹配的结果将字符串向右“滑动”尽量远的一段距离&＃xff0c;继续进行比较。
如上面的例子&＃xff0c;当第一次匹配到i&＃61;5&＃xff0c;j&＃61;5时&＃xff0c;出现不等&＃xff0c;S的下标不需要回溯到1&＃xff0c;j的下标也不需要回溯到0&＃xff0c;而是i继续保持5&＃xff0c;j的值变为2&＃xff08;因为next[5]&＃61;2&＃xff09;&＃xff0c;比较S[5]和T[2]。

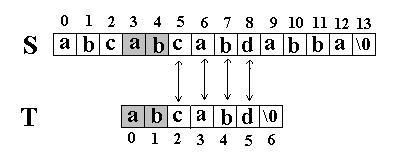
该算法的一个关键是next函数值。
next函数值的定义为&＃xff1a;
1&＃xff09;next[0]&＃61; -1
任何串的第一个字符的模式值规定为-1

2&＃xff09;next[j]&＃61; -1
模式串T中下标为j的字符&＃xff0c;如果与首字符相同&＃xff0c;且j的前面的1—k个字符与开头的1—k个字符不等&＃xff08;或者相等但T[k]&＃61;&＃61;T[j]&＃xff09;&＃xff08;1 ≤ k

3&＃xff09;next[j]&＃61;k
模式串T中下标为j的字符&＃xff0c;如果j的前面k个字符与开头的k个字符相等&＃xff0c;且T[j] !&＃61; T[k] &＃xff08;1 ≤ k

4&＃xff09;next[j]&＃61;0
剩下的其他情况。

next各值的含义&＃xff1a;
假设在字符串S中查找模式串T&＃xff0c;若S[m]!&＃61;T[n]&＃xff0c;则查看T[n]的模式函数值next[n]&＃xff1a;
1&＃xff09;next[n]&＃61; -1 表示S[m]和T[0]间接比较过了&＃xff0c;不相等&＃xff0c;下一次比较 S[m&＃43;1] 和T[0]
2&＃xff09;next[n]&＃61;0 表示比较过程中产生了不相等&＃xff0c;下一次比较 S[m] 和T[0]。
3&＃xff09;next[n]&＃61; k &＃xff08;0

next函数值的求取只与模式串有关&＃xff0c;程序如下&＃xff1a;

void get_next(const string T, int * next)
{int j &＃61; 0;int k &＃61; -1;next[0] &＃61; -1;int len&＃61;T.size ();while( j <len-1 ){if (k &＃61;&＃61; -1 || T[j] &＃61;&＃61; T[k]){&＃43;&＃43;j;&＃43;&＃43;k;if (T[j]!&＃61;T[k])next[j] &＃61; k;elsenext[j] &＃61; next[k];}elsek &＃61; next[k];}
}

获得next函数值后&＃xff0c;就可以根据next的值来进行字符串匹配

int KMP(const string S,const string T)
{int tlen &＃61; T.size ();int slen &＃61; S.size ();int *next&＃61;new int[tlen];get_next(T,next); //求next函数值int index&＃61;0,i&＃61;0,j&＃61;0;while(iif(S[i]&＃61;&＃61; T[j]){&＃43;&＃43;i; //继续比较后继字符&＃43;&＃43;j;}else{index &＃43;&＃61; j-next[j];if(next[j]!&＃61;-1)j&＃61;next[j]; //模式串向右移动else{j&＃61;0;&＃43;&＃43;i;}}} delete[] next;if(j&＃61;&＃61;tlen)return index; //匹配成功elsereturn -1;
}

综合上面的程序&＃xff0c;为&＃xff1a;

#include
#include
using namespace std;void get_next(const string T, int * next)
{int j &＃61; 0;int k &＃61; -1;next[0] &＃61; -1;int len&＃61;T.size ();while( j 1 ){if (k &＃61;&＃61; -1 || T[j] &＃61;&＃61; T[k]){&＃43;&＃43;j;&＃43;&＃43;k;if (T[j]!&＃61;T[k])next[j] &＃61; k;elsenext[j] &＃61; next[k];}elsek &＃61; next[k];}
}int KMP(const string S,const string T)
{int tlen &＃61; T.size ();int slen &＃61; S.size ();int *next&＃61;new int[tlen];get_next(T,next); //求next函数值int index&＃61;0,i&＃61;0,j&＃61;0;while(iif(S[i]&＃61;&＃61; T[j]){&＃43;&＃43;i; //继续比较后继字符&＃43;&＃43;j;}else{index &＃43;&＃61; j-next[j];if(next[j]!&＃61;-1)j&＃61;next[j]; //模式串向右移动else{j&＃61;0;&＃43;&＃43;i;}}} delete[] next;if(j&＃61;&＃61;tlen)return index; //匹配成功elsereturn -1;
}int main()
{string S &＃61; "abcabcabdabba";string T &＃61; "abcabd";int pos &＃61; KMP(S,T);cout<return 0;
}


参考整理自&＃xff1a;http://blog.csdn.net/lin_bei/article/details/1252686