支持向量回归删除异常值Python

支持向量回归&＃xff08;Support Vector Regression&＃xff0c;SVR&＃xff09;不仅可以用于预测&＃xff0c;还可以用于异常值检测。其基本思路是训练一个回归模型&＃xff0c;通过对每个数据点进行预测&＃xff0c;并计算其预测残差&＃xff0c;来判断该数据点是否为异常值。

在SVR中&＃xff0c;我们通过最大化预测出错的容忍度&＃xff08;margin&＃xff09;来寻找最优解。具体地&＃xff0c;我们希望找到一个超平面&＃xff0c;使得所有数据点到该超平面的距离都大于等于一定的阈值&＃xff08;margin&＃xff09;。对于线性回归模型&＃xff0c;该超平面为&＃xff1a;

w^T * x &＃43; b &＃61; 0


其中&＃xff0c;w是超平面法向量&＃xff0c;b是偏置项&＃xff0c;x是输入数据。对于一个输入数据x_i&＃xff0c;其距离超平面的距离为&＃xff1a;

y_pred_i - y_i &＃61; (w^T * x_i &＃43; b) - y_i


其中&＃xff0c;y_pred_i是该数据点的预测值&＃xff0c;y_i是该数据点的真实值。我们定义预测残差为绝对值&＃xff1a;

r_i &＃61; abs(y_pred_i - y_i)


那么&＃xff0c;如果某个数据点的预测残差&＃xff08;r_i&＃xff09;大于某个阈值&＃xff0c;则被视为异常值&＃xff0c;否则视为正常值。

在实际操作中&＃xff0c;我们需要指定SVR的一些超参数&＃xff0c;例如核函数类型、核函数参数、惩罚系数等。这些超参数对于SVR的性能有很大的影响&＃xff0c;需要根据具体问题进行调整。

sklearn.svm.SVR中fit函数常用参数如下&＃xff1a;

• X: 训练数据X&＃xff0c;必选参数&＃xff0c;形状为(n_samples, n_features)。
• y: 目标值y&＃xff0c;必选参数&＃xff0c;形状为(n_samples,)。
• sample_weight: 样本权重&＃xff0c;可选参数&＃xff0c;形状为(n_samples,)&＃xff0c;默认每个样本的权重相等。
• C: 惩罚系数&＃xff0c;可选参数&＃xff0c;默认为1.0&＃xff0c;一般取值为(0, &＃43;∞)之间的数。C越小&＃xff0c;模型越简单&＃xff1b;C越大&＃xff0c;模型越复杂。调整C的值可以防止过拟合或欠拟合的问题。
• kernel: 核函数&＃xff0c;可选参数&＃xff0c;默认为’rbf’&＃xff0c;表示高斯核函数。常用的核函数还有’linear’线性核函数、&＃39;poly’多项式核函数、‘sigmoid’ Sigmoid核函数。核函数的选择决定了模型的复杂度和拟合能力。
• degree: 多项式核函数的次数&＃xff0c;可选参数&＃xff0c;默认为3。
• gamma: 核函数系数&＃xff0c;可选参数&＃xff0c;默认为’scale’&＃xff0c;表示使用1 / (n_features * X.var())作为gamma值。也可以设置为’auto’或一个数值。
• coef0: 核函数的截距&＃xff0c;可选参数&＃xff0c;默认为0。
• epsilon: SVR中的ε&＃xff0c;可选参数&＃xff0c;默认为0.1。控制了对误差的容忍度。如果预测值与真实值的差小于ε&＃xff0c;该点就被视为预测正确。
• shrinking: 是否使用启发式&＃xff08;Hearst&＃xff09;方法来加速计算&＃xff0c;可选参数&＃xff0c;默认为True。建议保持默认值。
• tol: 迭代终止条件&＃xff0c;可选参数&＃xff0c;默认为1e-3。如果模型收敛后两次迭代的损失函数之差小于该值&＃xff0c;则终止训练。
• max_iter: 最大迭代次数&＃xff0c;可选参数&＃xff0c;默认为-1&＃xff0c;表示没有限制。如果收敛前达到该值&＃xff0c;则提前终止训练。
• cache_size: 核函数缓存大小&＃xff0c;可选参数&＃xff0c;默认为200MB。

需要根据具体的情况&＃xff0c;调整SVR的超参数以获得更好的性能和效果。

import pandas as pd
from sklearn.svm import SVR# 加载数据
data &＃61; pd.read_csv(&＃39;data.csv&＃39;)# 训练SVR模型
X &＃61; data.index.values.reshape(-1, 1)
y &＃61; data[&＃39;value&＃39;].values.reshape(-1, 1)
svr &＃61; SVR(kernel&＃61;&＃39;rbf&＃39;, gamma&＃61;&＃39;scale&＃39;, C&＃61;1.0, epsilon&＃61;0.1)
svr.fit(X, y)# 计算每个数据点的预测偏差
y_pred &＃61; svr.predict(X)
residuals &＃61; abs(y - y_pred)# 计算偏差的标准差
std_dev &＃61; residuals.std()# 计算阈值
threshold &＃61; 3 * std_dev# 找到异常值
mask &＃61; (residuals <&＃61; threshold).flatten()
clean_data &＃61; data.loc[mask]# 输出结果
print(clean_data)


测试报错&＃xff1a;
Reshape your data either using array.reshape(-1, 1) 。
dataframe数据需要转换为array。
经测试&＃xff1a;

X &＃61; df[&＃39;X&＃39;].values.reshape(-1, 1)
y &＃61; np.array(df[&＃39;y&＃39;])


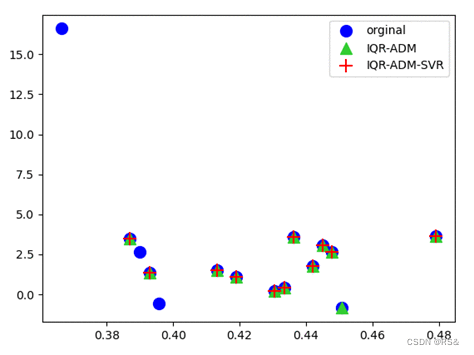
测试结果&＃xff1a;