怎样计算机翼升力大小,如何计算升力和阻力？

在流体流动模拟中，评估流体作用在固体上的力通常很重要，例如机翼或汽车上的升力和阻力。工程师可以通过评估这些物体上的力来量化设计的效率和空气动力学性能。今天，我们将讨论在 COMSOL Multiphysics 中计算升力和阻力的不同方法。

定义升力和阻力

当流体流过一个物体时，它会在物体表面施加一个力。如下图所示，垂直于流动方向的分力称为升力。平行于流动方向的分力称为曳力。为简单起见，我们假设流向与模型的坐标系对齐。稍后，我们将向您展示如何计算与模型坐标系不对齐的方向上的升力和阻力。

流体流过物体时升力和阻力分量的示意图。

升力和阻力有两个不同的来源——压力和黏性力。压力 通常称为压力梯度力，是由于表面压差而产生的力。黏性力 是由于摩擦力产生的力，作用于流体的相反方向。压力和黏滞力的大小有很大的不同，这取决于流体的类型。例如，行驶的汽车周围的气流通常是由压力控制的。

用总应力计算升力和阻力

在 COMSOL Multiphysics 中可以对所有内部变量进行访问，并通过边界积分轻松计算表面力。在这里，我们将演示如何计算 Ahmed 体上的阻力。您可以从我们的案例库中下载这个模型。

Ahmed 体上方气流的模拟。表面图显示了压力分布，流线的颜色表示速度大小。Ahmed 体后面的箭头表面显示了尾流区的环流。

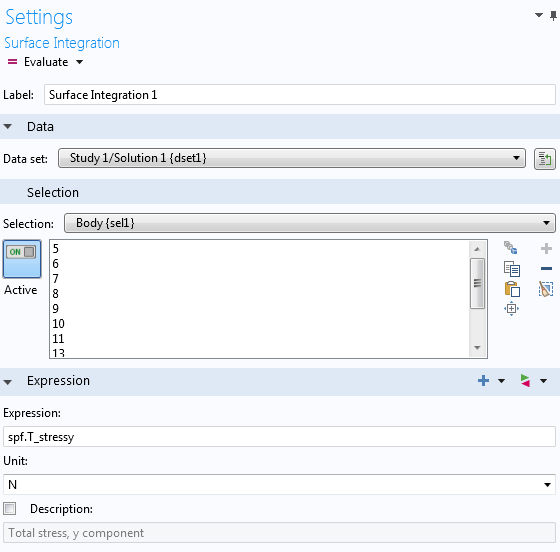
根据物理原理，有几种方法可以计算阻力。最直接的方法是在计算每个方向上的积分总应力——包括压力和黏性力的贡献。为此，我们首先需要在“派生值”节点下定义一个表面积分运算符，如下所示。

提示:另外，您也可以在组件耦合中使用边界探针或积分算子定义这种积分。不同之处在于，可以在模拟过程中使用在物理设置中定义的操作。例如，在优化研究中使用边界探针作为目标或约束来计算阻力。

接下来，我们可以选择边界来执行积分。在这个例子中，我们选择了物体上的所有边界。此模型中的升力位于 y-方向。我们可以输入表达式:spf.T_stressy，表示 y-方向上的总应力。

分别计算压力和黏性力

有时，工程师可以通过分别查看压力和黏性力来获得对设计更深入的了解。对于y-方向的黏性应力，COMSOL Multiphysics 提供了预定义的变量，spf.K_stressy。我们可以很容易地通过积分黏性应力来估算黏性力。

压力如何计算呢？压力由变量表示 p，是一个标量。为了向阻力的方向投射，需要用压力乘以表面法向量 spf.nymesh 的 y-分量。因此，我们可以通过积分 spf.nymesh*p 来评估表面上的压力。

在一些特殊的使用了壁函数的湍流中，使用摩擦速度 spf.u_tau 计算黏性力更加准精确。在 COMSOL Multiphysics 中，k-ε 和 k-ω 湍流模型使用壁函数。

如果需要了解更多关于 COMSOL Multiphysics 湍流模型的信息，请阅读我们的博客文章”我应该为我的 CFD 应用选择哪种湍流模型？“.

我们可以通过以下方法获得壁的局部剪应力:

u_\tau = \sqrt{\frac{\tau_w}{\rho}}

因此，局部剪应力在y-方向表示为:

\tau_{w_{y}} = \rho~u_\tau^2~\frac{u^T_y}{u^T}

其中，u^T 是壁的切向速度。我们可以进一步重新将 u^T 写作 u_\tau*u^+，其中 u^+ 是切向无量纲速度。

不需要在推导上花费太多精力，我们可以把前面的方程转换成 COMSOL 变量。我们可以使用下列表达式: spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus 积分阻力方向上的局部壁面剪应力(y-方向)。在这个表达式中，spf.rho 是流体的密度，spf.u_tangy 是壁在 y-方向上的速度，spf.uPlus 是切向无量纲速度。

下面的表格总结了用于计算每个力的表达式。

无壁函数的流体流动

有壁函数的湍流

压力

spf.nymesh*p

spf.nymesh*p

黏性力

-spf.K_stressy

spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus

总力

-spf.T_stressy

spf.nymesh*p + spf.rho*spf.u_tau*spf.u_tangy/spf.uPlus

注意:在这个例子中，阻力在 y-方向。您可能需要根据模型的方向更改投影方向。

攻角修正

通常，几何形状可能与流动方向不完全一致。几何中心参考线和引入流之间的角度称为攻角 (通常用希腊字母表示)。在航空航天工程中，经常使用攻角，因为它是翼型弦线和自由流方向之间的角度。下图显示了升力、阻力和机翼攻角之间的关系。

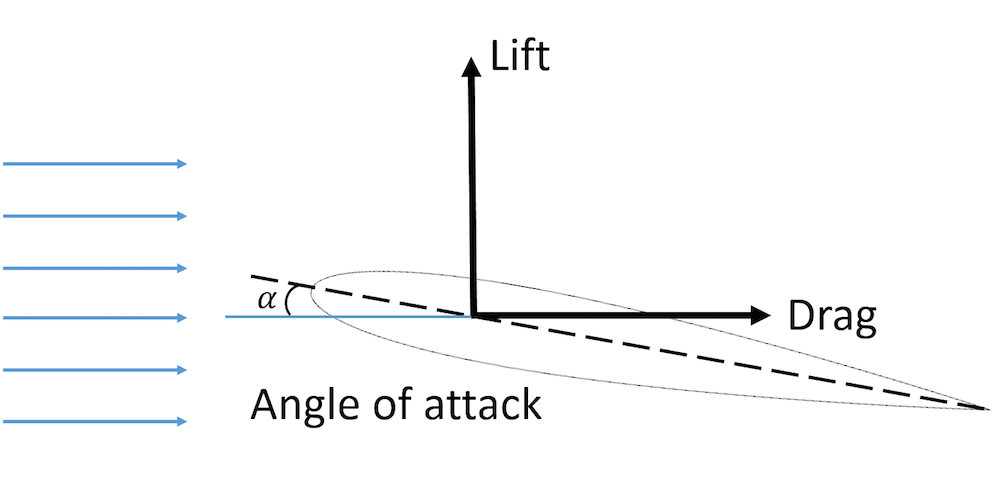
图翼上的升力、阻力和攻角的示意图。

以2D NACA 0012 型机翼为例，我们将向您展示如何用攻角修正来计算升力。这个模型可以在 COMSOL 案例库中找到。

有两种方法可以改变模型的攻角。我们可以旋转几何图形本身，也可以保持几何图形不变，但需要修改入口处的流向。在这里，我们将使用第二种方法。调整进气道边界条件的速度场要简单得多，因为我们不需要为每个攻角重新计算模型。如下图所示，翼型是固定的，而流线显示了由于调整进气速度方向而产生的攻角下的气流。

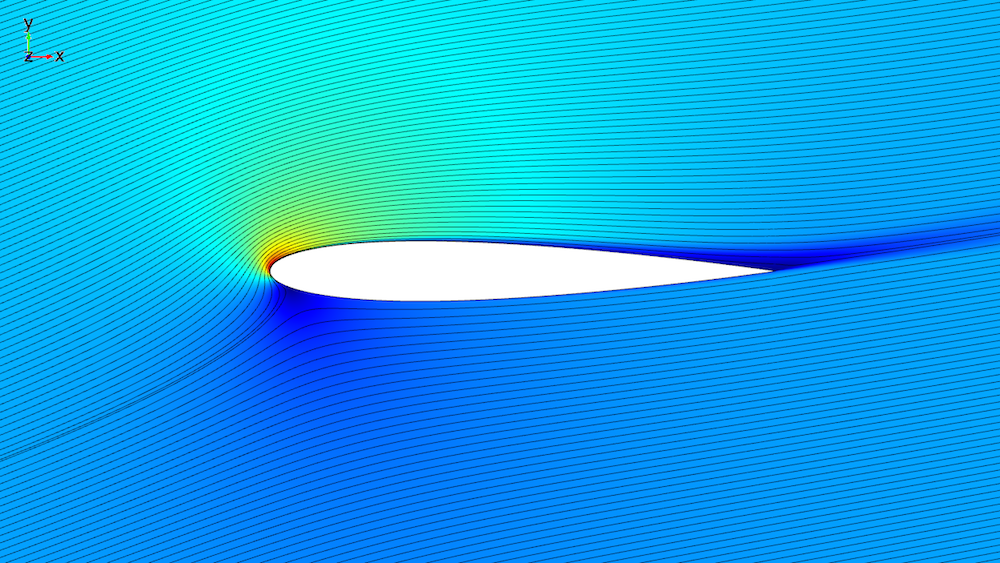
攻角为 14° 时，通过 NACA 0012 型机翼的气流模拟。表面图显示了速度大小以及流线(以黑色显示)。

这个示例使用了 SST 湍流模型，这个模型不使用壁函数。因此，我们将使用总应力来计算升力。在攻角为 0° 时，升力 -spf.T_stressy 很简单。如果攻角不为零，我们可以用下面的表达式把力投射到升力方向上: spf.T_stressx*sin(alpha*pi/180)-spf.T_stressy*cos(alpha*pi/180)。这里，α 代表攻角，单位为度。

升力或阻力系数如何计算呢？

你也可能对升力和阻力的无量纲形式——升力系数和阻力系数感兴趣。为了验证实验数据或者比较不同的设计，通常更容易使用系数来代替尺寸力。二维的升力系数定义为:

既然我们已经计算了空间升力，就可以使用动态压力和弦长简单地将力无量纲化。利用无量纲的升力系数，我们可以将模拟结果与实验数据进行比较(参考文献1).

注:在三维模拟中，升力系数是按面积而不是按长度无量纲化的: C_L = \frac{L}{\frac{1}{2} \rho u^2_\infty A}

不同攻角下，NACA 0012 机翼升力系数的模拟结果和实验数据的比较图。

如上图所示，在本模拟使用的攻角值范围内，计算结果和实验结果之间没有明显的差异。实验结果继续朝向机翼失速的攻角方向发展。

结束语

在这篇博客文章中，我们探索了计算 Ahmed 体和 NACA 0012 机翼升力和阻力的方法。我们演示了如何计算压力和黏性力，同时还研究了在湍流模型中使用壁函数的特殊情况。

我们在这里介绍的方法当然不限于这些特定的模拟。您可以计算任何边界或表面上的力，从而通过多物理场模拟获得对设计的理解。使用优化模块，您可以通过更进一步的分析，优化升力或阻力。

参考文献

C.L. Ladson, “Effects of Independent Variation of Mach and Reynolds Numbers on the Low-Speed Aerodynamic Characteristics of the NACA 0012 Airfoil Section,” NASA TM 4074, 1988.