Java实现优先队列：二叉堆详解

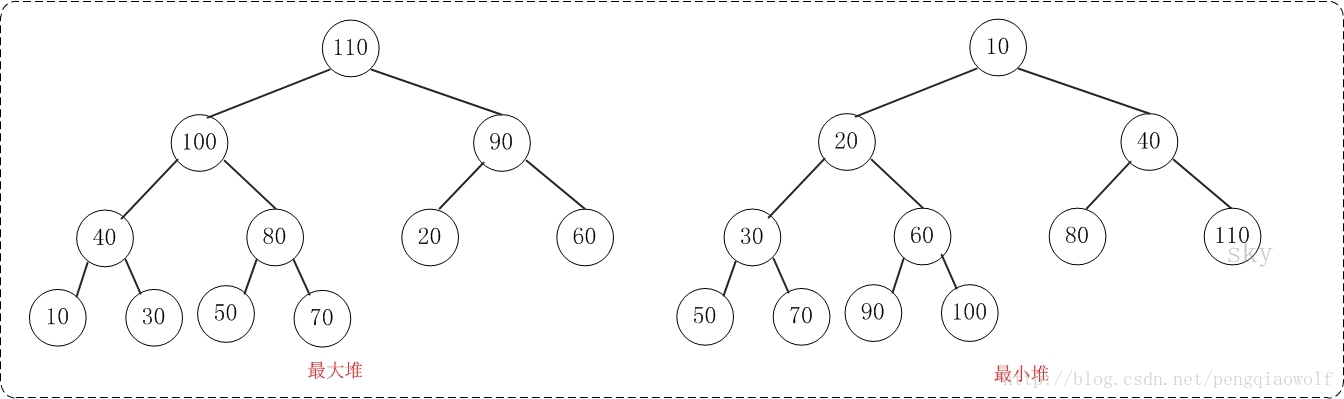
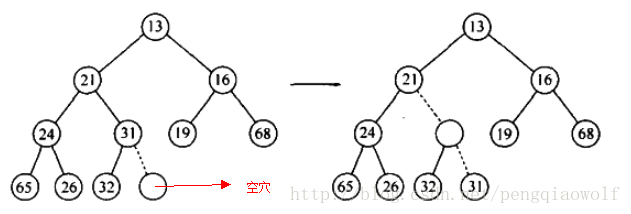
### 一、概念介绍 #### 1. 完全二叉树 完全二叉树是指除了最后一层外，所有其他层都是满的，并且最后一层的节点从左到右依次排列。 #### 2. 堆性质 - **最小堆**：父节点的值小于或等于其子节点的值。 - **最大堆**：父节点的值大于或等于其子节点的值。  由于二叉堆是完全二叉树，因此父节点和子节点的位置存在一定的关系。假设我们将二叉堆的第一个元素放在数组索引为1的位置，则父节点和子节点的位置关系如下： - 索引为i的左孩子的索引是 (2*i) - 索引为i的右孩子的索引是 (2*i+1) - 索引为i的父节点的索引是 (i/2) 因此，我们通常使用数组来实现二叉堆。 ### 二、实现思路 #### 1. 插入（上滤） - 在堆的末尾创建一个空穴。 - 如果新元素可以直接放入该空穴而不违反堆的性质，则插入完成。 - 否则，将空穴的父节点的值移入该空穴，空穴向上移动一步。 - 重复上述过程，直到新元素可以放入空穴中。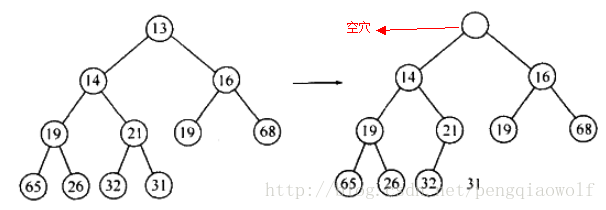  #### 2. 删除根元素（最小值/最大值）（下滤） - 将根节点删除，形成一个空穴。 - 将堆的最后一个元素移到空穴中。 - 如果该元素可以直接放入空穴而不违反堆的性质，则删除完成。 - 否则，将空穴的两个子节点中较小的一个移入空穴，空穴向下移动一步。 - 重复上述过程，直到该元素可以放入空穴中。  #### 3. 创建堆 - **简单方法**：使用N个相继的插入操作来构建堆，每个插入操作的时间复杂度为O(logN)，总时间复杂度为O(N logN)。 - **高效方法**：先保持堆的结构性，然后通过下滤操作确保堆的性质。这种方法的时间复杂度为O(N)。 ### 三、代码实现 ```java import java.util.ArrayList; /** * 头元素存储于1位置 * i节点的左孩子位置2*i，右孩子位置2*i+1，父亲位置i/2 */ public class BinaryHeap> { private ArrayList array; // 存储信息 private int currentSize; // 当前大小 public BinaryHeap() { array = new ArrayList<>(); array.add(null); } /** * 将数组转化为二叉堆 * @param array */ public BinaryHeap(ArrayList array) { currentSize = array.size(); for (int i = 1; i <= currentSize; i++) { this.array.set(i, array.get(i - 1)); // 保证结构性 } for (int i = currentSize / 2; i > 0; i--) { percolateDown(i); // 保证堆性 } } /** * 插入 * @param x */ public void insert(T x) { int hole = currentSize + 1; // 空穴的初始位置 array.add(x); for (; hole > 1 && x.compareTo(array.get(hole / 2)) <0; hole /= 2) { array.set(hole, array.get(hole / 2)); // 上滤 } array.set(hole, x); // 找到合适的位置 currentSize++; } /** * 查找最小元素 * @return */ public T findMin() { return array.get(1); } /** * 删除最小元素 * @return */ public T deleteMin() { if (currentSize <1) { System.out.println("BinaryHeap is Empty"); } T minElement = array.get(1); // 获取最小元素 array.set(1, array.get(currentSize)); // 将末尾元素存入 array.remove(currentSize--); // 移除最后元素，并使大小-1 if (currentSize > 0) { percolateDown(1); // 下滤 } return minElement; } /** * 删除任一元素 * @return 元素不存在，返回-1；删除成功，返回该元素的下标 */ public int delete(T x) throws Exception { if (currentSize <1) { throw new Exception("BinaryHeap is Empty"); } int index = array.indexOf(x); // 获取x的索引 if (index == -1) { return -1; } array.set(index, array.get(currentSize)); array.remove(currentSize--); percolateDown(index); // 下滤 return index; } /** * 下滤 */ public void percolateDown(int hole) { int child; T temp = array.get(hole); // 需要下滤的元素，临时存储 for (; hole * 2 <= currentSize; hole = child) { child = hole * 2; if (child 0) { child++; // child不为最后一个元素，且右元素小于左元素时：child为右元素，否则child为左元素 } if (temp.compareTo(array.get(child)) > 0) { array.set(hole, array.get(child)); // temp大于较小的元素，将空穴下滤一层 } else { break; // 找到合适的位置，跳出循环替换 } } array.set(hole, temp); } public static void main(String[] args) { int numItems = 1000; BinaryHeap h = new BinaryHeap<>(); int i = 37; for (i = 37; i != 0; i = (i + 37) % numItems) { h.insert(i); } for (i = 1; i