因为毕业论文是和贝叶斯理论相关的内容,今天恰巧看到一篇朴素贝叶斯分类算法的文章,写的非常通俗易懂,再结合另外一篇CNN的文章,在这里梳理一下,来帮助自己的理解。
朴素贝叶斯算法是基于朴素贝叶斯定理的一种算法。
在统计学中,贝叶斯的公式如下:
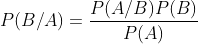
对于分类任务而言,我们都知道,一个分类器需要拿到某些事物的特征之后对其进行判断然后给出分类结果。其实,人类就是个高级分类器,比如,我们可以通过看妈妈的表情来判断出她今天开心还是不开心,于是妈妈的表情就是我们需要以此作为判断依据的特征——(眉头紧锁、嘟着嘴、眼睛放光、嘴角上扬等等),而开心和不开心就是最终的分类结果。
分类的数学定义就是:已知集合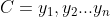 和
和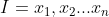 。现需要确定一个映射规则
。现需要确定一个映射规则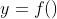 使得任意一个
使得任意一个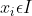 有且仅有一个
有且仅有一个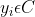 使得
使得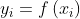 。
。
其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合(特征集合),其中每一个元素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f
那么根据上面的例子,不难看出,C中有两个类别(开心,不开心),I中有(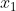 :眉头紧锁、嘟着嘴,
:眉头紧锁、嘟着嘴,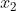 :眼睛放光、嘴角上扬)这两种待分类项。当然,在实际应用中,一个类别的输出是需要非常多特征来支撑的。
:眼睛放光、嘴角上扬)这两种待分类项。当然,在实际应用中,一个类别的输出是需要非常多特征来支撑的。
那么,贝叶斯是如何进行分类的呢?
首先看下贝叶斯分类算法的数学表达式
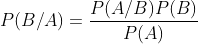
其实就是贝叶斯公式,只是这样无法看出该公式与分类之间的关系,实际上,在做分类时,做了如下的转换:

B代表类别,A代表特征(是一个集合),所以只要我们求出每个类别的P(类别|特征),再对比一下大小,就可以根据已有的特征得出我们想要的分类结果了。
我们就用原文中特征提取‘X’和‘O’的图举例说明吧

在分类的过程中,我们希望无论图像做何种变化(反转、扭曲、旋转,缩小放大等),都可以准确的提取到代表其类别的特征。通过CNN卷积核在图像上滑动来提取图像中的特征是一个非常有效的方法。
卷积是如何做到的呢?我们都知道图像是由千万个像素块组成的,对于灰白图像,每个像素块的值为0、1、-1 ,对于彩色图像而言,像素块值得范围是0-256,且是3通道得。这里得图像只有黑白两个色块, 假设1代表白色、-1代表黑色。

假定给cnn一张这样得X图,于是它可以通过左上角得卷积核对图像进行卷积操作,即从左到右、从上到下依次滑动, 滑动一次做一次卷积操作。 每个卷积核它都可以提取图中得一个特征,得到得结果即为特征图(feature map)。

可以看到,利用这种卷积核,最后得到的特征矩阵其中的值,越接近为1表示对应位置和卷积核代表的特征越接近,越是接近-1,表示对应位置和卷积核代表的反向特征越匹配,而值接近0的表示对应位置没有任何匹配或者说没有什么关联。
但是,我们为什么就要选这样的卷积核?好像有点刻意?实际上,卷积核中的参数起初并不是这样的,而是随机初始化,这里利用了反向传播算法,大白话就是,我先试探性的去猜测一些值,然后真实值给我的反馈是,我预测高了,那我就返回去将参数值调低一点,猜低了就调高点。所以就是通过这种以误差为指导去自适应地调整卷积核的值,来最小化模型预测值和真实值之间差异的目的。
回过头来,我们再说说P(类别|特征)是如何计算的,对于上面的例子,给定一张X图,假设它只提取到了特征1、特征2、特征3,当它输入贝叶斯分类器时,要判断它是不是X,也就是计算P(X|特征1、特征2、特征3)和P(O|特征1、特征2、特征3)谁的概率大。
在训练阶段,对于X的图像,当卷积核在图像滑动时,会提取到很多特征,如下所示:

所以假定在图片训练阶段,特征与分类结果的关系是:
| 特征1 | 特征2 | 特征3 | 特征4 | 特征5 | ... | X/O |
| 有 | 无 | 有 | 无 | 无 | X | |
| 有 | 有 | 有 | 有 | 有 | O | |
| 有 | 无 | 无 | 有 | 有 | O | |
| 有 | 有 | 有 | 有 | 有 | X | |
| 无 | 有 | 无 | 有 | 有 | X | |
| 无 | 无 | 无 | 有 | 有 | O | |
| 有 | 有 | 无 | 无 | 有 | X | |
| ... |
其中,分母P(特征1、特征2、特征3)=P(特征1)*P(特征2)*P(特征3),由于朴素贝叶斯法对条件概率分布做了条件独立性的假设,即每个特征都是相互独立的,故计算可以这样拆解。
于是P(特征1)=5/7;P(特征2)=4/7;P(特征3)=3/7。
分子:P(特征1、特征2、特征3|X)P(X)=P(特征1|X)*P(特征2|X)*P(特征3|X)*P(X) 所以,P(特征1|X)=3/4;P(特征2|X)=3/4;P(特征3|X)=2/4=1/2;P(X)=4/7。
P(X|特征1、特征2、特征3)=[(3/4)*(3/4)*(1/2)*(4/7)]/[(5/7)*(4/7)*(3/7)]
同理可得P(O|特征1、特征2、特征3)=[(2/3)*(1/3)*(1/3)*(3/7)]/[(5/7)*(4/7)*(3/7)]
明显P(X|特征1、特征2、特征3)>P(O|特征1、特征2、特征3)
结论:拥有特征1、特征2、特征3的这张图片,它是X图!
朴素贝叶斯分类的优缺点
优点:
(1) 算法逻辑简单,易于实现
(2)分类过程中时空开销小
缺点:
理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
参考:
https://zhuanlan.zhihu.com/p/26262151
https://zhuanlan.zhihu.com/p/50800849
加群,一起学习吧!


 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有