一维信号双边滤波器_双边滤波器文献总结（一）

因为最后的dde算法中&＃xff0c;最核心的就是滤波器模块&＃xff0c;由于做之前是没有好好攻读相关硬件文献&＃xff0c;加上相关背景写的不好导师一顿痛批&＃xff0c;搞得现在要本末倒置&＃xff0c;拿结果去找自己值得这么做的理由。但其实从研究角度来说应该是一件好事的。

(小吐个槽&＃xff1a;说起来之前也不算是没好好读文献&＃xff0c;实在是调研的时候方向偏差太大&＃xff0c;红外图像增强的VLSI或FPGA实现&＃xff1f;要么没有&＃xff0c;要么都停留在很简单的加速方式&＃xff0c;比如已经被做成ip的直方图均衡类算法&＃xff0c;甚至有人拿C转verilog来凑数的&＃xff01;有参考价值的都只是单单说算法而不是太讲实现的。也都是做rtl设计的时候遇着坑了&＃xff0c;才想到主要问题可能要去分析滤波器&＃xff0c;而搜滤波器的硬件实现才是真的一搜吓一跳&＃xff0c;果然很多时候&＃xff0c;我们思维都容易固化在顶层了&＃xff0c;毕竟做VLSI或者FPGA设计很多时候是没办法细份在某个具体应用领域的&＃xff0c;都是越通用越好&＃xff0c;而用它们加速本身也是一种底层思维&＃xff0c;迭代成本很高&＃xff0c;更需要我们具有这种底层的意识&＃xff09;。

今天就主要聊聊双边滤波器的硬件实现。

首先感觉比较新并且比较系统的应该算是这一篇了

Tseng Y C , Hsu P H , Chang T S . A 124 Mpixels/s VLSI Design for Histogram-Based Joint Bilateral Filtering[J]. IEEE Transactions on Image Processing, 2011, 20(11):3231-3241.

他最好的一点是对很多处理这种滤波器的思路进行了归类总结&＃xff0c;并对时间复杂度和存储消耗做了整理。

Support Pixel First Approach

我最后的采用的设计方法&＃xff0c;也是非常相似于Durand的方法&＃xff0c;所以我先对这种类型做一说明。双边滤波器拥有更多的应用场景就是因为他比一般的空间滤波器&＃xff08;文中称spatial filter&＃xff09;有更好的边缘保持性(edge-preserving)&＃xff0c;理解一下就是边缘&＃xff08;也可以理解为轮廓&＃xff09;越多的地方&＃xff0c;平滑的程度相对于非边缘区域小一点。一般的空间滤波器&＃xff0c;在FPGA和VLSI应用中&＃xff0c;已经有了很好办法了&＃xff0c;就是用寄存器组&＃xff0c;搭建一个卷积核&＃xff0c;并且利用S行缓冲把zig-zag&＃xff08;写Z字母的顺序&＃xff09;的顺序&＃xff0c;变成S行并行。&＃xff08;图画的很丑&＃xff0c;大家理解&＃xff09;

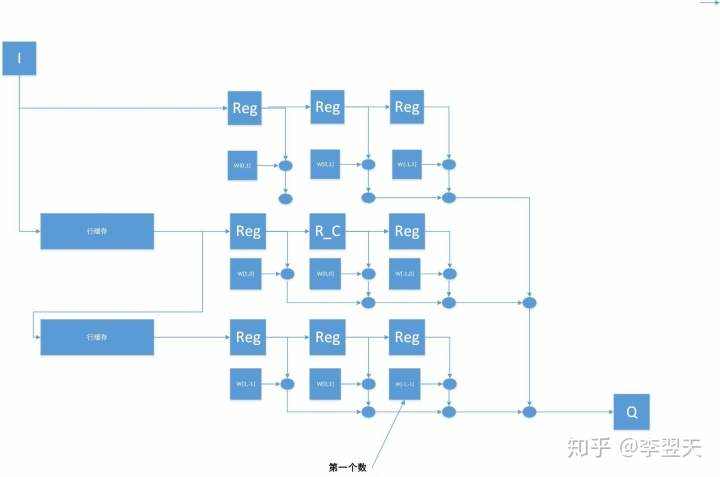
那么能不能把f(|c-q|),g(|Ic-Iq|)也写到这个卷积核里呢&＃xff1f;答案是不能的&＃xff0c;由于位置确定&＃xff0c;计算f其实输入都是常量&＃xff0c;但是g的输入可不是常量&＃xff0c;他需要中心像素点&＃xff0c;而这个卷积核每移动一下&＃xff08;整个运算操作可以等效为卷积核按Z型移动&＃xff09;&＃xff0c;中心像素点都会变。g需要一个单输入超越函数运算模型&＃xff0c;在硬件实现中&＃xff0c;方法有3&＃xff0c;一种是多项式分解&＃xff0c;一种是cordic算法&＃xff0c;一种就是LUT&＃xff08;查找表&＃xff09;。前两个这个表中没有&＃xff0c;就不说了&＃xff0c;LUT顾名思义&＃xff0c;就是有限输入情况&＃xff0c;你拿着输入翻译成地址到RAM里找&＃xff0c;1个周期就能实现&＃xff0c;特别适合现在的情况&＃xff1a;时间短、吞吐率一致&＃xff0c;而且数字图像处理的灰度级本身也是有限的。但是套的时候就发现问题了&＃xff0c;我为了简单只话了一个3x3的卷积核&＃xff0c;如果大了&＃xff0c;对于RAM面积就是几何倍的增长&＃xff0c;如何能让这个增长不太大就是去缩减Ic-Iq的灰度级&＃xff08;subsample&＃xff09;&＃xff0c;或者用线性插值&＃xff08;piecewise-linear&＃xff09;去进一步简化LUT&＃xff08;y&＃61;c--->y&＃61;ax&＃43;b&＃xff09;。当然也有人直接避开这种计算&＃xff0c;比如Paris的方法是直接用近似的方法把二维卷积化成了三维卷积&＃xff08;比较怪异不细说&＃xff09;。memory cost应该没有表里这样&＃xff0c;就basic而言我觉得应该是这样的&＃xff0c;不少于S*&＃xff08;N-1&＃xff09;&＃43;(S*&＃xff08;h&＃43;1&＃xff09;)^2&＃xff0c;第一项是行缓冲&＃xff0c;第二项是查找表加寄存器组&＃xff08;查找表深度h&＃xff09;。

Target Pixel First Approach

我理解的这样的归类方法应该是不做卷积核了&＃xff0c;把整个拆解成一维卷积&＃xff0c;Pham的方法里简要论证了一下&＃xff0c;直接一维卷积做行不行&＃xff0c;但也是说是approximation&＃xff0c;效果咋样见仁见智&＃xff0c;

但是一维以后复杂度可是降了很多个层次&＃xff0c;能用上盒子滤波器就再好不过了&＃xff08;box-filter&＃xff09;。可能是受这个启发&＃xff0c;表里后面的几种方法都在简化维度的同时&＃xff0c;让这个approximation做的更接近一点。本文作者也就是主要借鉴了Porikli的方法&＃xff0c;文中称IH&＃xff08;intergral histogram&＃xff09;,我很细致的去阅读了一下这篇文章&＃xff0c;其本质还是去用多项式分解的形式化解g的运算&＃xff0c;只是不依赖卷积核了&＃xff0c;用内存把所有位置直方图积分结果存储起来&＃xff0c;卷积核(kernel)内的直方图&＃xff0c;直接可以用四个位置的结果计算出来&＃xff0c;利用他的分解方式套入计算g。令我比较疑惑的一点&＃xff0c;直方图化以后&＃xff0c;他便无法考量卷积核内的位置了&＃xff0c;但是按照双边滤波器定义&＃xff0c;即便两个像素相等&＃xff0c;一个若在左侧&＃xff08;3x3举例&＃xff09;&＃xff0c;一个在右上侧&＃xff0c;他们的权值应该是不等的&＃xff0c;文章里好像是直接按相等做近似了。。。那也差的太多了。优点就在于只用存直方图积分结果&＃xff0c;和原图。复杂度上降低了很多。