一阶系统开环传递函数表达式_【推荐阅读】导弹自抗扰姿态控制系统设计

点击上方“蓝字”关注“战术导弹技术”！

摘要：为了使姿态控制系统在模型不确定以及存在干扰的情况下仍具有较强的鲁棒性，提出了自抗扰姿态控制系统设计方法。首先，建立了一般姿态控制系统的数学模型。其次，设计了自抗扰姿态控制系统模型，通过研究自抗扰姿态控制系统回路频带特性，分析了扩张观测器频带对控制性能的影响，并给出了控制参数的设计原则。最后，对自抗扰姿态控制系统进行数学仿真验证。仿真结果表明:相比于传统的带PI校正的姿态控制系统，自抗扰姿态控制系统能获得更好的控制效果，使系统的跟踪性能，抗干扰能力进一步提升。

关键词：自抗扰控制;扩张观测器;姿态控制系统;频域分析;战术导弹

随着战术导弹速度的不断提高，导弹姿态控制面临的典型问题是高不确定性、强耦合、快时变、严重非线性。针对该问题，目前工程上应用较为成熟的控制方法有带“PI校正”姿态控制、基于极点配置的状态反馈控制等。这些方法均是基于误差反馈的控制方法，属于传统的PID控制，而当系统受到较大干扰力矩且干扰力矩变化较快，或者模型存在不确定时，将难以获得好的控制品质。崔世海等综述了导弹控制系统设计方法，在上述传统控制系统设计方法的基础上，提出了现代控制系统设计方法以及综合设计方法，一定程度解决了通道间耦合以及控制系统非线性问题，但是在现阶段，其设计方法结构复杂，需要的信息多，不利于工程化实现。

本文在传统控制系统设计的基础上，采用自抗扰控制技术，将导弹受到的耦合干扰、气动系数偏差以及总体结构偏差等所有不确定因素当作“总的未知扰动”，通过扩张状态观测器进行估计并加以补偿，消除了单一姿态控制系统存在的响应速度慢，抗干扰能力弱的问题，从而降低了通道间耦合效应，且便于工程实现。在本文设计过程中，进一步考虑舵机动力学，将其建立到扩张状态观测器方程中，为快速估计出不确定量，将经过舵机动力学的舵指令作为观测器输入从而实现更大带宽下的稳定回路。

0 1姿态控制系统数学模型

姿态控制系统的典型结构如图1所示，从图1可以看出，典型的姿态控制系统一般由角速度阻尼回路和姿态角主反馈回路两部分组成，控制系统的输入指令是姿态角指令(θ_c)。回路中的角速度信号由角速度陀螺测得，而姿态角信号(θ)可以由姿态陀螺或角速度陀螺信号经积分得到。

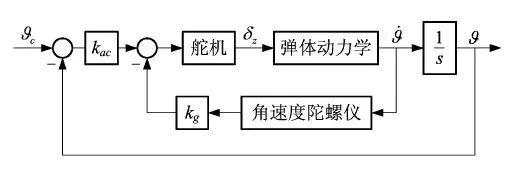
图1 典型姿态控制系统原理框图

由系数冻结法得线性化后的弹体动力学方程组为：

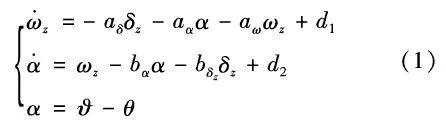
当不考虑模型的不确定时，式(1)两边取拉普拉斯变换，可推导出由舵控指令δ_z到姿态角速度的传递函数为：

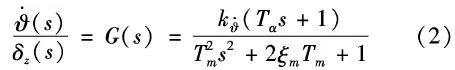
0 2基于ESO的姿态控制系统设计

下面给出稳定回路自抗扰控制器的设计过程。

令δ_z=u，模型的不确定性和干扰为d₁、d₂，系统可以表示为：

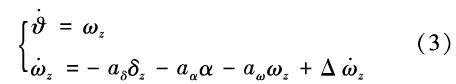
根据系统动力学方程式(3)可写出其对应的状态方程为：

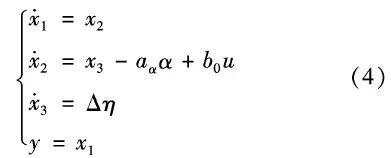
根据式(4)可建立导弹姿态控制系统俯仰方向的扩张状态观测器方程为：

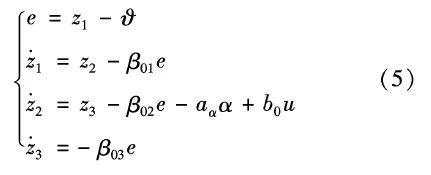
假设观测器的带宽ω_ESO，则观测器增益选取为：

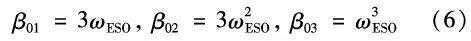
确定观测器的带宽后ω_ESO，即可确定三个增益系数。

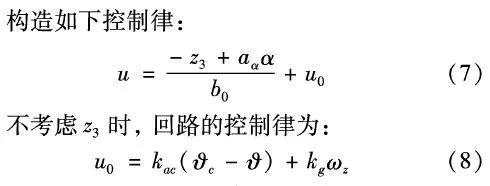
假设控制器带宽为ω_c，则特征多项式为：

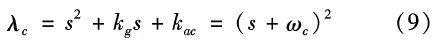
则控制器参数为k_ac=ω_c²，k_g=2ω_c，确定控制器的带宽，即可确定线性反馈控制器的参数。

由此，可以得到自抗扰姿态控制系统工作原理框图如图2所示。相比于传统的姿态控制系统，自抗扰姿态控制系统用ESO将模型不确定性及干扰进行估计并补偿到舵指令中，提高了系统的抗干扰能力。

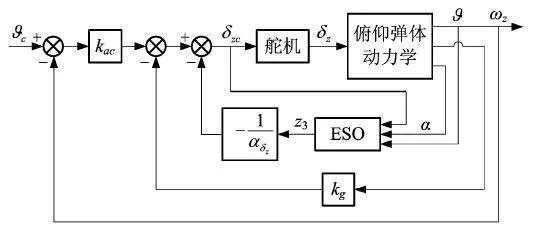
图2 自抗扰姿态控制原理框图 

0 3自抗扰稳定回路特性分析

由图2可以求得自抗扰姿态控制系统的闭环传递函数为：

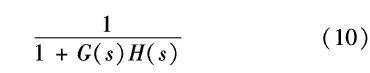
如前所述，k_g、k_ac与控制器带宽ω_c有关，由闭环传递函数可知，当系统稳定时，可使系统的闭环增益为1，即严格响应跟踪指令。系统的稳定性与所设计的参数有关，可采用劳斯判据对稳定性进行判别，即由式(10)闭环传递函数可以得到系统特征方程为D(s)=1+G(s)H(s)，系统的设计目的是使该特征方程所有根均具有负实部，此时系统稳定。

在表达式(10)中，可以设计的参数为控制器带宽ω_c和观测器带宽ω_ESO(ESO频率)，下文研究ω_c与ω_ESO对整个系统的影响。对此分为两种情况讨论，分别为在扩张观测器中考虑舵机动力学补偿与不考虑舵机动力学补偿。

(1)当不考虑舵机动力学补偿时，扩张观测器状态方程为：

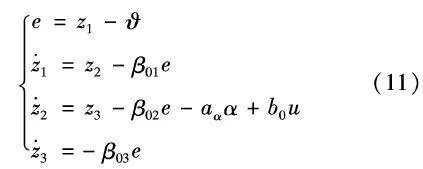
扩张状态观测器结构框图如图3所示。由图3可知，扩张状态观测器的输入量分别是系统的输入量δ_z和输出量θ，它利用系统的输入和输出信息对系统模型不确定性以及内部的干扰进行估计。对观测器方程式(11) 进行拉普拉斯变换并消元整理可得观测器输入量到输出量z₃传递函数为：

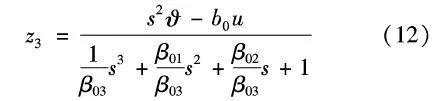
由式(12) 可知，对于系统的模型不确定性及干扰角加速度的估计量，本质上就是将其经过一个低通滤波器滤波后得到的结果。

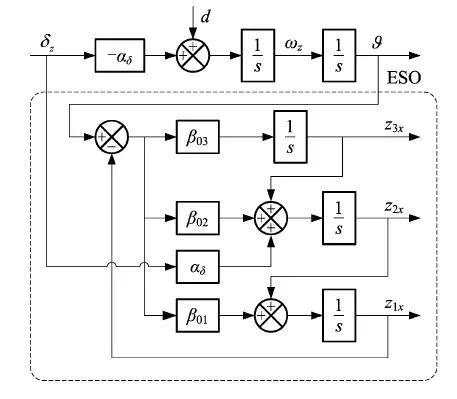
图3 ESO结构图

(2)当考虑舵机动力学补偿时，假设舵机为二阶动力学特性，其传递函数为：

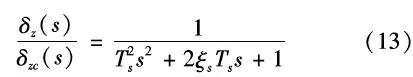
扩张观测器状态方程为：

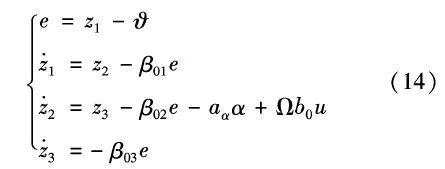
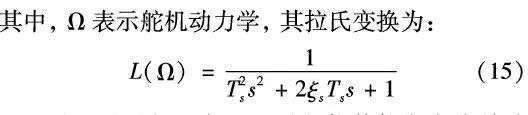
对观测器方程式(14) 进行拉普拉斯变换并消元整理可得观测器输入量到输出量z₃传递函数为：

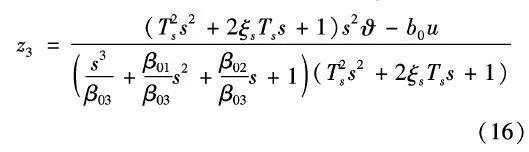
即若在观测器中考虑舵机动力学，ESO输入的舵指令变为经过舵机动力学后的指令。

3.1 稳定回路稳定特性

由上述分析可知，稳定回路的特性取决于控制器带宽ω_c和观测器带宽ω_ESO。对于扩张观测器中不包含舵机动力学的情况，取ω_c=2.5Hz，令ω_ESO从1Hz变化到100Hz，得到系统幅值裕度、相位裕度随ESO频率变化曲线如图4、图5所示。

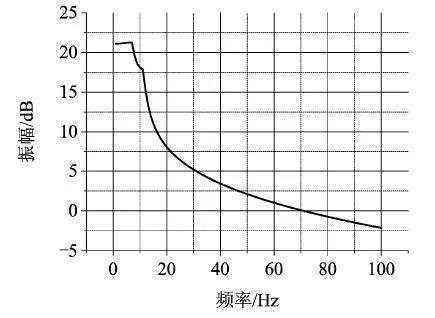
图4 幅值裕度随ESO频率变化曲线

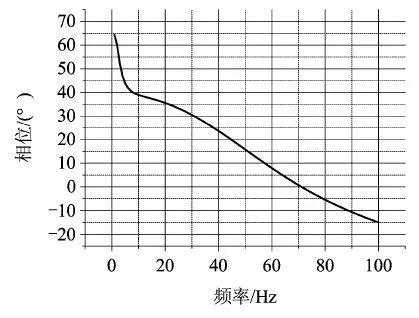
图5 相位裕度随ESO频率变化曲线

由图4、图5可知，当不将舵机动力学补偿到扩张观测器中时，系统幅值裕度与相位裕度随扩张观测器频率的增加而降低，在观测器频率到70Hz左右时，系统幅值裕度和相位裕度开始小于零，系统失稳。

若将舵机动力学补偿到扩张观测器中，同样取ω_c=2.5Hz，令ω_ESO从1Hz变化到100Hz，得到系统幅值裕度、相位裕度随ESO频率变化曲线如图6、图7所示。

图6 幅值裕度随ESO频率变化曲线

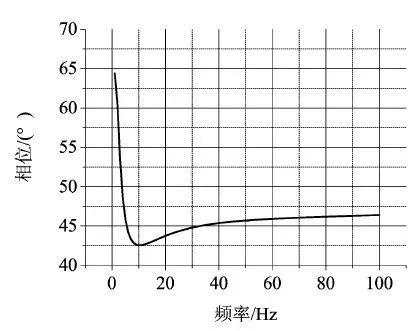
图7 相位裕度随ESO频率变化曲线

由图6、图7可知，若将舵机动力学补偿到扩张观测器中，系统幅值裕度与相位裕度随扩张观测器频率的增加在一定范围内迅速降低，超出一定范围时，系统幅值裕度与相位裕度随扩张观测器频率的增加维持在较稳定的区间内，即随着观测器频率的增加系统不会失稳。

取观测器频率为70Hz，分别在不考虑舵机补偿和考虑舵机补偿情况下得到系统的开环伯德图如图8、图9所示，若不加舵机动力学补偿，系统的幅值裕度0.104dB， 相位裕度0.834°；加入舵机动力学补偿，系统的幅值裕度7.94dB，相位裕度46.2°。可以看出，在扩张观测器中考虑舵机动力学补偿，可使原系统在趋于临界稳定的状态时变为稳定，并且增加了系统的稳定区域。

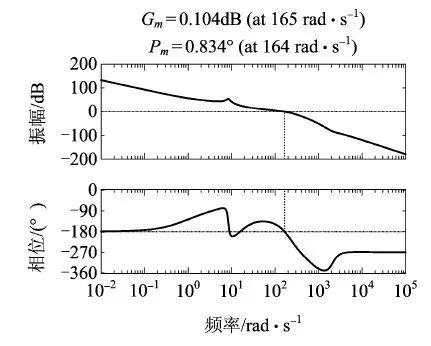
图8 不考虑舵机补偿系统伯德图

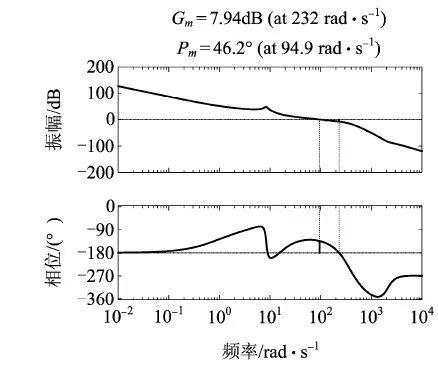
图9 考虑舵机补偿系统伯德图

3.2 稳定回路抗扰特性

考虑ESO对舵机动力学的补偿，当系统存在干扰时，即系统引起角加速度的变化存在一个干扰项，得到系统的闭环阶跃响应如图10所示，可以看出，当存在干扰时，如果不对控制指令进行前馈补偿，系统的阶跃响应会存在一个常值偏差，当对控制指令进行前馈补偿时，系统阶跃响应不存在偏差且动态特性更好。

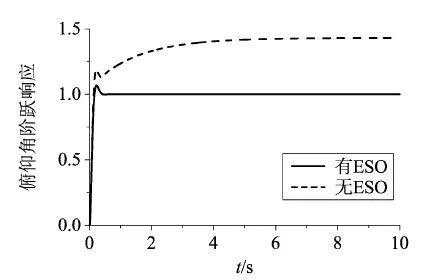
图10 系统阶跃响应

取控制系统频率ω_c=2.5Hz，依次改变ESO频率为1Hz、10Hz和50Hz，干扰大小为97.2s^-2，得到干扰估计以及系统的阶跃响应曲线如图11、图12所示，由图11、图12可知，随着观测器频率的增大，对干扰的估计速度提高，系统阶跃响应曲线的超调量减小，从而更好的跟踪指令。

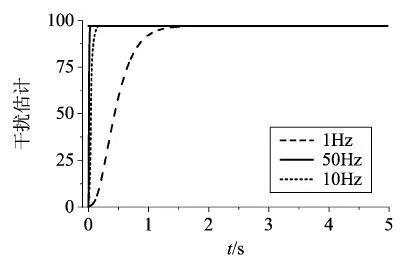
图11 干扰估计

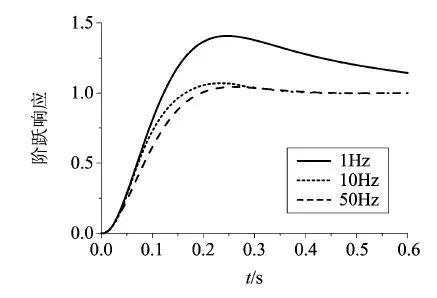
图12 系统阶跃响应

3.3 自抗扰控制器参数确定原则

由上述分析可知，ω_c和ω_ESO对姿态控制系统的稳定性、抗扰性具有重要影响。本节依据上述分析，并结合工程实际，提出如下自抗扰姿态控制系统参数的确定原则。

在确定观测器带宽时，应同时考虑对干扰的估计速度以及系统的稳定裕度，观测器带宽越大，响应速度越快，扰动的抑制能力越强，但会使系统稳定裕度降低，尤其是不考虑舵机动力学补偿时，系统可能失稳。据此，在姿态控制系统的设计过程中，可以先确定控制器带宽ω_c，使系统具有一般的跟踪指令能力，然后加入扩张观测器对系统的模型不确定性及干扰进行估计，补偿到控制指令中。观测器带宽ω_ESO的选取，既要使控制系统能够快速的抑制干扰，又能保持系统一定的稳定裕度，根据文献的推导，一般选取ω_ESO=(3~5)ω_c。

0 4仿真分析

为了验证自抗扰姿态控制系统的控制性能，在表1所示的典型弹体气动参数下，通过数值仿真分析系统的跟踪性能、稳定性能及抗干扰性能，并与传统控制算法进行对比。

表1 典型弹体参数

基于上述设计原则，经过调试选取控制系统带宽ω_c=16rad/s，扩张观测器带宽ω_ESO=62.8rad/s，为了与传统PI校正比较，设计传统PI校正控制系统与自抗扰控制系统带宽相同，传统PI控制器参数为：

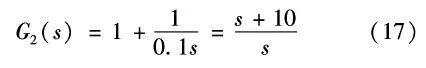
4.1 跟踪性能分析

为了评价系统的跟踪能力，给定期望姿态角为1°，给出系统阶跃响应曲线，如图13所示。由图13中曲线可知，自抗扰控制(ADRC)调节时间0.27s，超调量4.5%，传统PI控制调节时间0.69s，超调量43%，可以看出，自抗扰控制的跟踪效果明显好于传统PI控制。

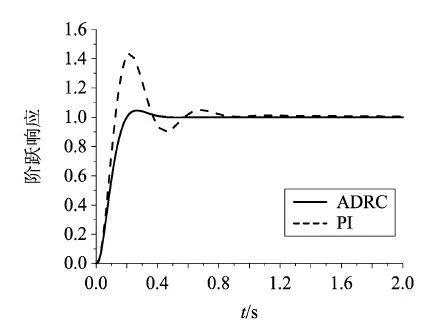
图13 两种控制下单位阶跃响应

4.2 稳定性能分析

图14给出了在两种控制器作用下系统的开环伯德图，表2给出了两种控制算法的稳定裕度对比结果。

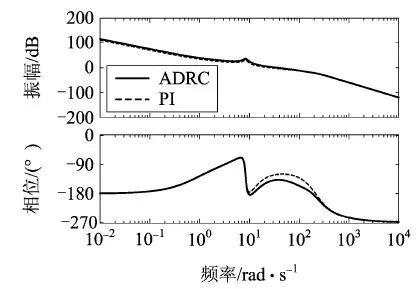
图14 两种控制器下伯德图

表2 两种控制器下稳定裕度对比

图14和表2结果显示，相比于传统PI控制，采用自抗扰控制时系统的稳定裕度略有降低，但可以满足系统的稳定性要求。

4.3 抗干扰性能分析

当系统存在干扰时，干扰大小为2×a_δ=97.2s^-2，系统无输入指令，得到干扰后输出的闭环响应曲线如图15所示，可以看出两种控制器最终都能将干扰消除，采用自抗扰控制器能够更快的消除偏差且干扰引起的偏差的幅值更小，更有利于系统的动态响应；系统存在干扰时，得到的姿态角指令到姿态角的阶跃响应如图16所示，可以明显看出，采用自抗扰的控制器系统的动态响应更好。

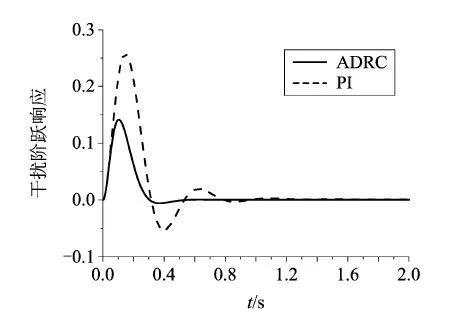
图15 干扰的阶跃响应

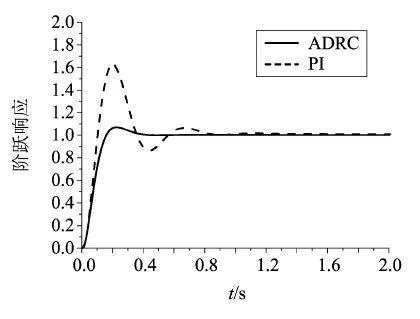
图16 存在干扰时系统的阶跃响应

0 5结论

设计了自抗扰姿态控制系统，并对控制性能进行了仿真分析，得到结论如下:

(1)在姿态控制系统中加入自抗扰控制器对模型不确定性以及干扰进行补偿，提高了系统的鲁棒性。

(2)若在自抗扰控制器中考虑舵机动力学的补偿，可以增加系统的稳定带宽，使系统无论在观测器高频带还是低频带都保持一定的稳定裕度。

(3)通过分析观测器与控制器带宽对回路稳定特性的影响，得出自抗扰控制器参数的确定原则:ω_ESO的选取既要使控制系统能够快速的抑制干扰，又能使系统保持一定的稳定裕度，根据经验，一般选取。ω_ESO=(3~5)ω_c。

(4)仿真结果表明，自抗扰姿态控制系统与传统的带PI校正的控制系统相比，其跟踪性能、抗干扰性能都有明显的提升。

[引用格式]张文杰,阮聪,夏群利,等.导弹自抗扰姿态控制系统设计[J].战术导弹技术,2019，(6): 67-73+98.

本文选自《战术导弹技术》2019年第6期

作者：张文杰,阮聪,夏群利,周建平

转载请务必注明出处

版权所有，违者必究

《战术导弹技术》

《战术导弹技术》由中国航天科工集团有限公司主管，中国航天科工飞航技术研究院主办，北京海鹰科技情报研究所承办，是为导弹的研究、设计、制造、试验、使用等服务的学术期刊。刊物创刊于1980年，为双月刊，是“中文核心期刊”“中国科技核心期刊”，在国内外公开发行。刊物主要刊登导弹和导弹武器系统总体技术、任务规划技术、推进技术、制导、导航与控制技术等方面的学术论文。

通讯地址：北京7254信箱4分箱(100074)

电话：(010)68375662(编辑)

            (010)68375084(发行)

邮箱：zhanshu310@126.com

网址：www.haiying.org.cn

欢迎投稿