主要内容:
1. 行列式按行(列)展开
即:某行元素 X 自己的代数余子式 = 行列式D的值
2. 异乘变零定理
即:某行元素 X 另一行元素的代数余子式 = 0
3.行列式相乘定理
1.1按行展开(1.可以降阶)
(2.选择0多的行或者列展开)因为需要乘以这个元素本身
余子式:去掉某一元素所在的行和列后,将剩下的元素按原来的顺序排列成新的行列式,这个行列式就叫做被去掉元素的余子式。用M表示余子式
如下图为 M32 的余子式,即原行列式 3行2列元素的余子式

代数余子式:前面多一个符号,3+2表示所在行列,用A 表示代数余子式
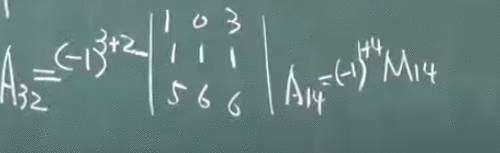
(按某行展开)
i 行的每个元素和他自己的代数余子式的乘机和 就是行列式的值
D = 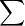 某行元素 X 自己的代数余子式
某行元素 X 自己的代数余子式
D = 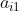
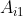 +
+ 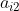
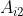 +……+
+……+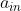
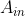
小写的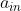 是某一行的元素(第 i 行的元素)
是某一行的元素(第 i 行的元素)
大写的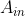 是这个元素对应的(他自己的)代数余子式
是这个元素对应的(他自己的)代数余子式
(按某列展开)也一样
D = 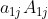 +
+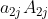 +……+
+……+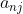

某行元素与另一行元素的代数余子式相乘,乘机之和等于0
图一:用第四行的元素与第一行的代数余子式相乘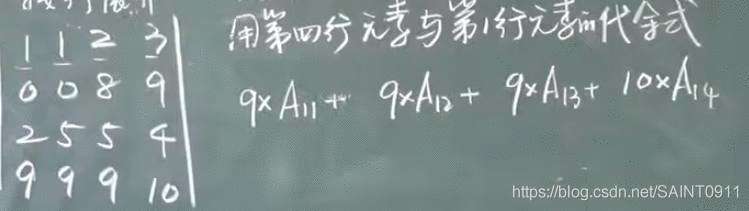
图一
图二:按第一行展开

图二
此时,此行列式的值 D= 某行元素 X 自己的代数余子式。同时,根据行列式的性质,行列式两行相等,值为0
按第一行展开:
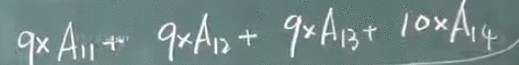
图一与图二展开相同,因此图一的结果也为0
拉普拉斯定理:
定义:
K阶子式:任意取K行,K列,交叉线上的元素

2阶子式余子式,去掉子式所在行和列,剩余的子式
代数余子式,前面加符号(去掉的行列放在一起1+2+1+2)
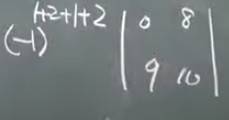
拉普拉斯展开定理:(某些特殊的行列式用此定理展开是比较容易的)
任意取定K行,由K行元素组成的所有K阶子式与代数余子式乘 机之和,等于行列式D的值
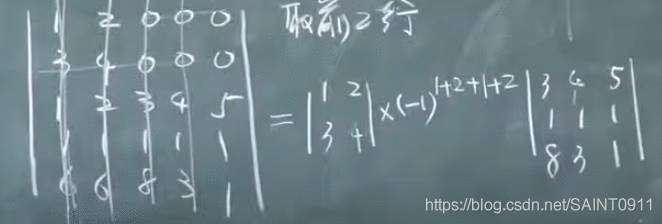
比如,取两行时,对应地该取两列。但在该行列式中,只有取1,2两列时,才不是0。等于0就不用算了。因此该行列式的值如上图所示
3.1行列式相乘定理同阶行列式才能用这个定理来做题
行列式相乘:与矩阵相乘一样
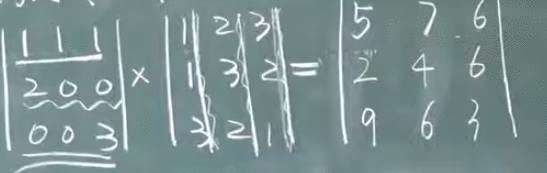
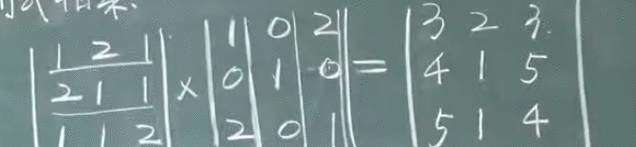
如下图所示 的不同阶的行列式相乘时,可以直接把单个的行列式先算出来再相乘
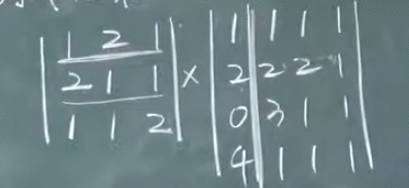

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有