使用线段树解决Luogu1471方差问题

题目来源：Luogu1471
这是一道典型的数据结构题目，需要处理区间方差的计算，并支持区间修改。初看可能会觉得棘手，但通过合理的数学转换和线段树的应用，可以有效地解决问题。

题目给出的方差公式为：

其中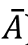， 表示平均值。为了便于处理，我们可以将方差公式展开：

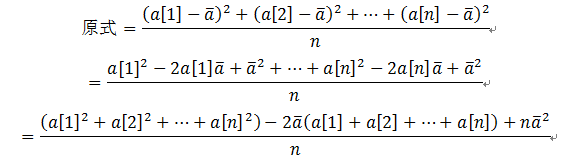
注意到中间项 a[1]+a[2]+...+a[n] 可以简化为 平均值 * n，因此进一步化简得：

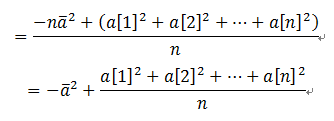
基于上述公式，我们只需要在线段树中维护两个信息：区间的和以及区间的平方和。对于区间修改，假设我们要在区间内增加一个值 v，则更新规则如下：

在懒惰标记（Lazy Tag）传递时，根据上述规则调整即可。此外，虽然分块方法也是一种可行的解决方案，但本篇主要讨论线段树的实现。

以下是具体的C++代码实现：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int n, m, lt[400001], rt[400001];
double t[400001], pt[400001], a[100001], add[400001];
inline double sqr(double x) { return x * x; }
inline void clean(int nod) {
    if (!add[nod]) return;
    if (lt[nod] != rt[nod]) {
        pt[nod*2] += 2 * add[nod] * t[nod*2] + sqr(add[nod]) * (rt[nod*2] - lt[nod*2] + 1);
        pt[nod*2+1] += 2 * add[nod] * t[nod*2+1] + sqr(add[nod]) * (rt[nod*2+1] - lt[nod*2+1] + 1);
        t[nod*2] += (rt[nod*2] - lt[nod*2] + 1) * add[nod];
        t[nod*2+1] += (rt[nod*2+1] - lt[nod*2+1] + 1) * add[nod];
        add[nod*2] += add[nod];
        add[nod*2+1] += add[nod];
    }
    add[nod] = 0;
}
inline void build(int l, int r, int nod) {
    lt[nod] = l; rt[nod] = r; add[nod] = 0;
    if (l == r) {
        t[nod] = a[l];
        pt[nod] = sqr(a[l]);
        return;
    }
    int mid = l + r >> 1;
    build(l, mid, nod*2);
    build(mid + 1, r, nod*2 + 1);
    t[nod] = t[nod*2] + t[nod*2 + 1];
    pt[nod] = pt[nod*2] + pt[nod*2 + 1];
}
inline void update(int i, int j, double v, int nod) {
    clean(nod);
    if (lt[nod] >= i && rt[nod] <= j) {
        add[nod] += v;
        pt[nod] += 2 * v * t[nod] + sqr(v) * (rt[nod] - lt[nod] + 1);
        t[nod] += (rt[nod] - lt[nod] + 1) * v;
        return;
    }
    int mid = lt[nod] + rt[nod] >> 1;
    if (i <= mid) update(i, j, v, nod*2);
    if (j > mid) update(i, j, v, nod*2 + 1);
    t[nod] = t[nod*2] + t[nod*2 + 1];
    pt[nod] = pt[nod*2] + pt[nod*2 + 1];
}
inline double sum(int i, int j, int nod) {
    clean(nod);
    if (lt[nod] >= i && rt[nod] <= j) return t[nod];
    int mid = lt[nod] + rt[nod] >> 1;
    double ans = 0;
    if (i <= mid) ans += sum(i, j, nod*2);
    if (j > mid) ans += sum(i, j, nod*2 + 1);
    return ans;
}
inline double squareSum(int i, int j, int nod) {
    clean(nod);
    if (lt[nod] >= i && rt[nod] <= j) return pt[nod];
    int mid = lt[nod] + rt[nod] >> 1;
    double ans = 0;
    if (i <= mid) ans += squareSum(i, j, nod*2);
    if (j > mid) ans += squareSum(i, j, nod*2 + 1);
    return ans;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%lf", &a[i]);
    build(1, n, 1);
    for (int i = 1; i <= m; i++) {
        int p, x, y;
        scanf("%d%d%d", &p, &x, &y);
        if (p == 1) {
            double z;
            scanf("%lf", &z);
            update(x, y, z, 1);
        } else {
            double a1 = sum(x, y, 1) / (double)(y - x + 1);
            if (p == 2) printf("%.4lf\n", a1);
            else {
                double a2 = squareSum(x, y, 1) / (double)(y - x + 1);
                printf("%.4lf\n", a2 - sqr(a1));
            }
        }
    }
    return 0;
}