作者:ck凯悦风_855 | 来源:互联网 | 2024-10-18 19:32
图基本概念及操作一、思维导图二、重要概念笔记1.图的定义图(Graph)G由顶点集合V(G)和边集合E(G)构成。图可分为有向图和无向图。2.图的存储结构一、邻接矩阵:二、邻接表;
图基本概念及操作
一、思维导图
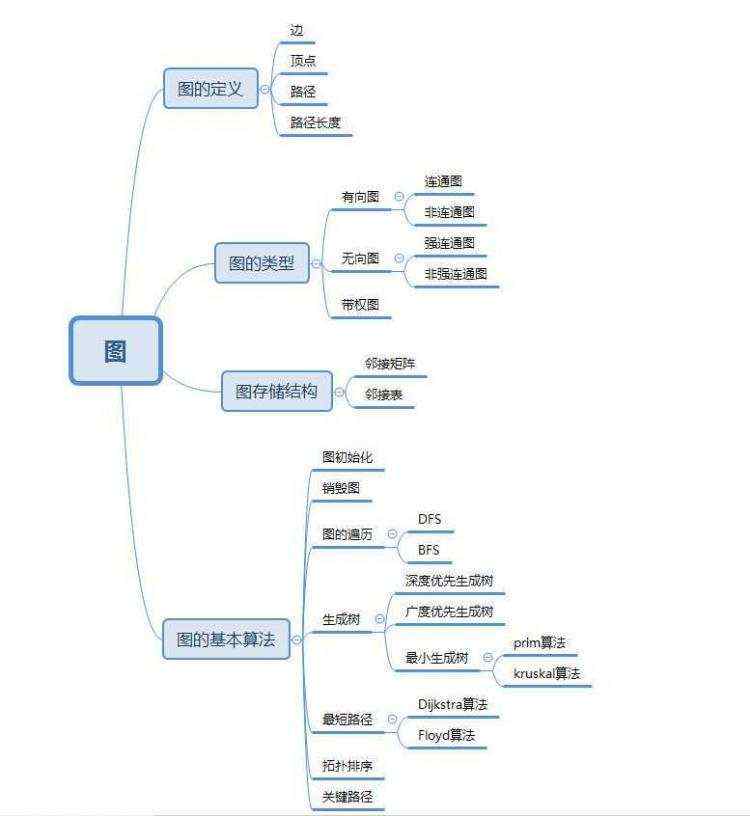
二、重要概念笔记
1.图的定义
图(Graph)G由顶点集合V(G)和边集合E(G)构成。图可分为有向图和无向图。
2.图的存储结构
一、邻接矩阵:
#define MAXVEXNUM 顶点数
//点,边
typedef int VexType;
typedef int ArcCell;
typedef struct {
VexType vexs[MAXVEXNUM];//点的集合
ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
int vexNum, arcNum;
}MyGraph;
二、邻接表;
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
} ArcNode;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct
{ VNode adjlist[MAXV] ; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
三、邻接矩阵图的创建:
void CreateGraphFromConsole(MyGraph &G, int vexNum, int arcNum)
{
G.vexNum = vexNum;
G.arcNum = arcNum;
for (int i = 0; i {
for (int j = 0; j {
G.arcs[i][j] = 0;//初始化
}
}
printf("Please input %d vex name:\n",vexNum);
//输入点的信息
for (int i = 0; i {
printf("i=%d ", i);
cin >> G.vexs[i];
}//输入边的的信息
for (int j = 0; j {
int x, y; ArcCell value;
cout <<"请输入x点、y点的值及x到y的边的值:" < cin >> x; cin >> y; cin >> value;
cout <<" x=" <3、图的遍历DFS算法思想:大概意思就是从某个点一直往深处走,走到不能往下走之后,就回退到上一步,直到找到解或把所有点走完。
BFS算法思想:
从某个点一直把其邻接点走完,然后任选一个邻接点把与之邻接的未被遍历的点走完,如此反复走完所有结点。类似于树的层序遍历。
4.最小生成树
prim算法;
#define INF 32767 //INF表示∞
#define MAXV 顶点数
void Prim(MyGraph g,int v)//v是最开始的顶点
{
int lowcost[MAXV];
int min;
int closest[MAXV], i, j, k;
for (i = 0; i {
lowcost[i] = g.edges[v][i];
closest[i] = v;
}
for (i = 1; i {
min = INF;
for (j = 0; j if (lowcost[j] != 0 && lowcost[j] {
min = lowcost[j];
k = j; //k记录最近顶点编号
}
printf(" 边(%d,%d)权为:%d\n",closest[k],k,min);
lowcost[k] = 0; //标记k已经加入U
for (j = 0; j if (lowcost[j] != 0 && g.edges[k][j] {
lowcost[j] = g.edges[k][j];
closest[j] = k;
}
}
}
5、最短路径
Dijkstra算法:时间复杂度度:o(n^2);
void Dijkstra(MatGraph g,int v)
{ int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0;i { dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i] path[i]=v; //顶点v到i有边时
else
path[i]=-1; //顶点v到i没边时
}
s[v]=1; //源点v放入S中
for (i=0;i { mindis=INF;
for (j=0;j if (s[j]==0 && dist[j] { u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入S中
for (j=0;j if (s[j]==0)
if (g.edges[u][j] { dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
三、疑难问题及解决方案:
1.图着色问题
疑难1:如何对两点间颜色进行判断
解决方案:定义一个数组color [vex]//vex为顶点数+1;color[0] 不用
疑难二:如何判断方案中的颜色种类。
方法:对颜色种类进行排序。使其有序,比便于计算颜色种类。计算重复的颜色树,用输入颜色数删去重复颜色数即可得到颜色的种类。
代码如下:
#include
using namespace std;
#define MAXVEXNUM 501
//点,边
typedef int VexType;
typedef int ArcCell;
typedef struct {
VexType vexs[MAXVEXNUM];//点的集合
ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
int vexNum, arcNum;
int color[MAXVEXNUM];
}MyGraph;
void Creategraph(MyGraph& G, int vexNum, int arcNum);
void program(MyGraph& G,int color);
int Check(MyGraph& G,int color);
int main()
{
MyGraph G;
int vexNum, arcNum;
int color;
cin >> vexNum >> arcNum>>color;
Creategraph(G, vexNum, arcNum);
program(G,color);
}
void Creategraph(MyGraph& G, int vexNum, int arcNum)
{
int x, y;
G.vexNum = vexNum;
G.arcNum = arcNum;
for (int i = 1; i <= vexNum; i++)
{
for (int j = 1; j <= vexNum; j++)
{
G.arcs[i][j] = 0;//初始化
}
}
for (int i = 0; i {
cin >> x >> y;
G.arcs[x][y] = 1;
}
}
void program(MyGraph& G,int color)//方案
{
int i, j, n;
cin >> n;
for (i = 0; i {
for (j = 1; j <= G.vexNum; j++)
{
cin >> G.color[j];
}
if (Check(G,color))
{
cout <<"Yes" < }
else
{
cout <<"No" < }
}
}
int Check(MyGraph& G, int color)//判断
{
int flag = 1;
int count = 0, tmp;
int a[MAXVEXNUM] = { 0 };
for (int i = 1; i <= G.vexNum; i++)
{
a[i] = G.color[i];
}
for (int i = 0; i {
for (int j = 1; j {
if (a[j] > a[j + 1])
{
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
}
for (int i = 1; i {
if (a[i] == a[i + 1])
count++;
}
if (G.vexNum-count > color)
return 0;
for (int i = 1; i <= G.vexNum; i++)
{
for (int j = 1; j <= G.vexNum; j++)
{
if (G.arcs[i][j])
{
if (G.color[i] == G.color[j])
{
flag = 0;
break;
}
}
}
}
return flag;
}
排序算法也可换成查找排序或者其他高效的排序算法。