批标准化
批标准化&＃xff08;batch normalization,BN&＃xff09;是为了克服神经网络层数加深导致难以训练而诞生的。深度神经网络随着深度加深&＃xff0c;收敛会越来越慢&＃xff0c;会导致梯度弥散问题&＃xff08;vanishing gradient problem&＃xff09;。
统计机器学习有一个ICS理论&＃xff0c;这是一个经典假设:源域和目标域的数据分布是一致的。
解决思路是根据训练样本和目标样本的比例对训练样本做一个矫正。
方法
批标准化一般用在非线性映射&＃xff08;激活函数&＃xff09;之前&＃xff0c;对x&＃61;Wu&＃43;b做规范化&＃xff0c;使结果&＃xff08;输出信号各个维度&＃xff09;的均值为0&＃xff0c;方差为1&＃xff0c;让每一层的输入有一个稳定的分布会有利于网络的训练。
优点&＃xff1a;加快收敛速度&＃xff0c;容易跳出局部最小值&＃xff0c;一定程度上缓解过拟合。
示例
对每层的Wx_plus_b进行批标准化&＃xff0c;这个步骤放在激活函数之前&＃xff1a;
#计算的均值和方差&＃xff0c;其中axes&＃61;[0]表示想要标准化的维度
fc_mean,fc_var&＃61;tf.nn.moments(Wx_plus_b,axes&＃61;[0],)
scale&＃61;tf.Variable(tf.ones([out_size]))
shift&＃61;tf.Variable(tf.zeros([out_size]))
epsilon&＃61;0.001
Wx_plus_b&＃61;tf.nn.batch_normalization(Wx_plus_b,fc_mean,fc_var,shift,scale,epsilon)
#也就是在做&＃xff1a;
#Wx_plus_b&＃61;&＃xff08;Wx_plus_b-fc_mean&＃xff09;/tf.sqrt(fc_var&＃43;0.001)
#Wx_plus_b&＃61;Wx_plus_b*scale&＃43;shift
神经元函数及优化方法 激活函数
激活函数&＃xff08;activation function&＃xff09;运行时激活神经网络中某一部分神经元&＃xff0c;将激活信息向后传入下一层的神经网络。
激活函数不会改变输入数据的维度&＃xff0c;即输入和输出维度一样。
TF有以下激活函数&＃xff1a;
平滑非线性的激活函数&＃xff1a;sigmoid、tanh、elu,softplus和softsign,即tf.nn.softplus()等等
连续但是不是处处可微的函数&＃xff1a;relu、relu6、crelu和relu_x&＃xff0c;即tf.nn.relu()等等
随机正则化函数dropout&＃xff1a;tf.nn.dropout(),防止过拟合&＃xff0c;用来舍弃某些神经元
relu是目前最受欢迎的激活函数。
a&＃61;tf.constant([-1.0,2.0])
with tf.Session() as sess:b&＃61;tf.nn.relu(a)print(sess.run(b))
[ 0. 2.]
dropout函数&＃xff1a;一个神经元将以概率keep_pro决定是否被抑制&＃xff1b;如果被抑制&＃xff0c;该神经元的输出就是0,如果不被抑制&＃xff0c;那么该神经元的输出值将被放大到原来的1/keep_pro倍。
a&＃61;tf.constant([[-1.0,2.0,3.0,4.0]])
with tf.Session() as sess:b&＃61;tf.nn.dropout(a,0.5,noise_shape&＃61;[1,4])print(sess.run(b))b &＃61; tf.nn.dropout(a, 0.5, noise_shape&＃61;[1, 1])print(sess.run(b))
[[-0. 4. 6. 8.]]
[[-2. 4. 6. 8.]]
小结&＃xff1a;
当输入数据特征相差明显时&＃xff0c;用tanh的效果会很好。
当输入数据特征相差不明显时&＃xff0c;用sigmoid的效果会很好。
现在大部分卷积神经网络采用relu作为激活函数&＃xff0c;其他的有用tanh&＃xff0c;尤其在NLP上。
卷积函数
卷积函数是构建神经网络的重要支架。
以下分别说明&＃xff1a;
1.计算N维卷积的和的函数tf.nn.convolution()
tf.nn.convolution(input,filter,padding,strides&＃61;None,dilation_rate&＃61;None,name&＃61;None,data_format&＃61;None)
2.对一个四维的输入数据input和四维的卷积核filter进行操作&＃xff0c;然后对输入数据进行一个二维的卷积操作&＃xff0c;最后得到卷积之后的结果。
tf.nn.conv2d(input,filter, strides, padding, use_cudnn_on_gpu&＃61;None, name&＃61;None)
input:为一个Tensor&＃xff0c;数据类型必须是float32或者float64&＃xff1b;
filter:为一个tensor,数据类型必须是与input输入的数据类型相同&＃xff1b;
strides:一个长度是4的一维整数类型数组&＃xff0c;每一维度对应的是input中每一维的对应移动步数&＃xff1b;如strides[1]对应input[1]的移动步数&＃xff1b;
padding&＃xff1a;一个字符串&＃xff0c;取值为SAME或者VALID&＃xff1b;‘SAME&＃39;适用于全尺寸操作&＃xff0c;即输入数据维度和输出数据维度相同&＃xff1b;&＃39;VALID&＃39;适用于部分窗口&＃xff1b;
use_cudnn_on_gpu:一个可选布尔值&＃xff0c;默认情况下是True;
name:为这个操作取一个名字&＃xff1b;
import tensorflow as tf
import os
import numpy as np
input_data&＃61; tf.Variable(np.random.rand(10,9,9,3),dtype&＃61;np.float32)
filter_data&＃61;tf.Variable(np.random.rand(2,2,3,4),dtype&＃61;np.float32)
y &＃61; tf.nn.conv2d(input_data,filter_data,strides&＃61;[1,3,3,1],padding&＃61;&＃39;SAME&＃39;)
print(&＃39;输入的结果为&＃xff1a;&＃39;, y)
输入的结果为&＃xff1a; Tensor("Conv2D:0", shape&＃61;(10, 3, 3, 4), dtype&＃61;float32)
3.函数tf.nn.depthwise_conv2d(input, filter, strides, padding, name&＃61;None,data_format&＃61;None)
input的数据维度[batch,in_height,in_weight,in_channels]
filter的维度[filter_height, filter_width,in_channel, channel_multiplierl]
在通道in_channels上面的卷积深度是3&＃xff0c;
将不同的卷积核独立地应用在in_channels的每条通道上&＃xff0c;
然后将所有的结果进行汇总&＃xff0c;输出通道的总数&＃xff0c;in_channel*channel_multiplier
4.函数tf.nn.separable_conv2d(input, depthwise_filter, pointwise_filter, strides, padding, name&＃61;None,data_format&＃61;None)
利用几个分离的卷积核去做卷积。
depthwise_filter:为一个张量&＃xff0c;数据维度是四维[filter_height, filter_width, in_channels, channel_multiplier]
pointwise_filter:一个四维的张量&＃xff0c;数据维度是四维[1,1,channel_multipliter*in_channels,out_channels]。
pointwise_filter是在depthwise_filter卷积之后的混合卷积&＃xff1b;
strides:一个长度是4的一维整数类型数组&＃xff0c;每一个维度对应的是input中每一维的对应移动步数
5)函数tf.nn.atrous_conv2d(value, filters, rate, padding, name&＃61;None)计算Atrous卷积&＃xff0c;称为扩张卷积
(6)函数tf.nn.conv2d_transpose(value, filter, output_shape,strides, padding&＃61;&＃39;SAME&＃39;,data_format&＃61;&＃39;NHWC&＃39;,name&＃61;None)为conv2d的转置。
(7)函数tf.nn.conv1d(value, filters, stride, padding , use_cudnn_on_gpu&＃61;None,data_format&＃61;None,name&＃61;None)与二维卷积类似
该函数用来计算给定三维的输入和过滤器的情况下的一维卷积。
输入为三维&＃xff0c;[batch, in_width, in_channels]
卷积核的维度为三维&＃xff0c;少了一维filter_heigth,如[filter_width,in_channels, out_channels].
stride是一个正整数&＃xff0c;代表卷积核向右移动每一步的长度。
(8)函数tf.nn.conv3d(input, filter, strides, padding, name&＃61;None)与二维卷积类似。
用来计算给定五维的输入和过滤器的情况下的三维卷积
与二维卷积相对比&＃xff1a;
input的shape中多了一维in_depth,形状为[batch, in_depth, in_height, in_width, in_channels]
filter的shape中多了一维filter_depth,[filter_depth, filter_height, in_channel,channel_multiplierl]构成卷积核大小
strides的shape中多了一维strides_depth, [strides_batch, strides_depth, strides_height, strides_width, strides_channel]
(9)函数tf.nn.conv3d_tranpose(value, filter, output_shape, strides, padding&＃61;&＃39;SAME&＃39;,name&＃61;None)与二维反卷积类似。
池化函数
在神经网络中&＃xff0c;池化函数一般跟在卷积函数的下一层。池化分为最大池化和平均池化两种。每个池化操作的窗口大小由ksize指定&＃xff0c;并根据步长stride决定移动步长。
(1).tf.nn.avg_pool(value,ksize,strides,padding,data_format&＃61;&＃39;NHWC&＃39;,name&＃61;None) 计算池化区域中元素的平均值
def avg_pool(value, ksize, strides, padding, data_format&＃61;&＃39;NHWC&＃39;, name&＃61;None)
value:是一个四维的张量&＃xff0c;数据维度是[batch, height, width, channels]
ksize:是一个长度不小于4的整型数组&＃xff0c;每一位上的值对应于输入数据张量中每一维的窗口对应值
strides:一个长度不小于4的整型数组&＃xff0c;该参数指定滑动窗口在输入数据张量每一维上的步长
padding&＃xff1a;一个字符串&＃xff0c; 取值为SAME或者VALID
data_format:&＃39;NHWC&＃39;代表输入张量维度的顺序&＃xff0c;N为个数&＃xff0c;H为高度&＃xff0c;W为宽度&＃xff0c;C为通道数
name:为这个操作取一个名字&＃xff1b;
(2)tf.nn.max_pool(value,ksize, strides, padding, data_format&＃61;&＃39;NHWC&＃39;, name&＃61;None)
计算池化区域中元素的最大值
(3).tf.nn.max_pool_with_argmax(input, ksize, strides, padding ,Targmax&＃61;None, name&＃61;None)
计算池化区域中元素的最大值和该最大值所在的位置
(4).tf.nn.avg_pool3d()和tf.nn.max_pool3d()
分别为在三维下的平均池化层和最大池化层
(5).tf.nn.fractional_avg_pool()和tf.nn.fractional_max_pool()
分别为在三维下的平均池化和最大池化
(6)tf.nn.pool()执行一个N维的池化操作
&＃xff08;https://www.sogou.com/link?url&＃61;DOb0bgH2eKh1ibpaMGjuy9i2Gol-5JTB43wDyFcvlbGHDDTl0xsUWrBn4VA8J3Sxh3Iic7Mnfz-YMEr0L5a9ww..&＃xff09;
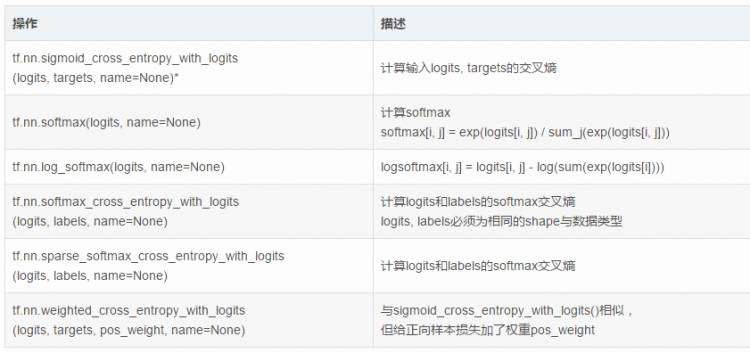
分类函数
优化方法
重点有8个&＃xff0c;如下&＃xff1a;
tf.train.GradientDescentOptimizer()
tf.train.AdadeltaOptimizer()
tf.train.AdagradOptimizer()
tf.train.AdagradDAOptimizer()
tf.train.MomentumOptimizer()
tf.train.AdamOptimizer()
tf.train.FtrlOptimizer()
tf.train.RMSPropOptimizer()
&＃xff08;具体&＃xff1a;https://blog.csdn.net/imfengyitong/article/details/70808544&＃xff09;
京公网安备 11010802041100号