▽算子公式证明_最优化导论(MachineLearning)机器学习中所用的基础数学公式总结...

Day 2

人工智能必需的线性代数&＃xff0c;微积分部分基础公式整理

• 生成子空间概念

         令V表示Rn的一个子集&＃xff0c;如果V在向量加和运算以及标量乘积运算下是封闭的 那么称V为Rn的子空间

         也即&＃xff0c;如果a和b是V中的向量&＃xff0c;那么a&＃43;b或者∂a(∂为任意标量)也为V中的向量

         假定a1, a2, a3, ......, ak为Rn中的任意向量&＃xff0c;他们所有线性组合的集合成为(a1, a2, a3, ......, ak)的生成子空间

         记做&＃xff1a;span[a1, a2, a3, ......, ak] &＃61; {∑i&＃61;1~k ∂iai: a1, a2, a3, ......, ak ∈ R}

         对于向量a&＃xff0c;生成子空间span(a1, a2, a3, ......, ak)由向量∂a组成&＃xff0c;∂为任意实数(∂ ∈ R)同理&＃xff0c;若a可以表示为a1, a2, ......, ak的线性组合&＃xff0c;则有&＃xff1a;

                span[a1, a2, ......, ak, a] &＃61; span[a1, a2, ......, ak]

• 基&＃xff0c;标准基

         给定子空间V&＃xff0c;如果存在线性无关的向量集合{a1, a2, ......, ak}  ⊂ V 使得V&＃61; span[a1, a2, ......, ak]那么称{a1, a2, ......, ak}是子空间V的一组基 子空间中所有基都有相同数量的向量&＃xff0c;这一适量成为V的维数&＃xff0c;记做dim V.

• 矩阵的秩Rank

         m * n维的矩阵A &＃61;  [a11, a12, ......, a1n]

                                         [a21, a22, ......, a2n]

                                         [:,          :, .........,    :]

                                         [am1, am2, ......, amn]

         A的第K列 ak &＃61; [a1k, a2k, ......, amk]T

         矩阵A中线性无关列的最大数目称为矩阵A的秩&＃xff0c;rank A

         *rank A为span[a1, a2, ......, an]的维数

         矩阵A的行数等于列数&＃xff0c;则称该矩阵为方阵&＃xff0c;行列式为与每一个方阵A相对应的一个标量. 记为det A或者&＃xff5c;A&＃xff5c;

         行列式性质&＃xff1a;1.矩阵A &＃61; [a1, a2, ......, an]的行列式为各列的线性函数&＃xff0c;即&＃xff0c;对任意的∂,ß ∈ R 和ak(1), ak(2) ∈ Rn 都有&＃xff1a;

1. det[a1, ..., ak-1, ∂ak(1) &＃43; ßak(2),  ak&＃43;1, ... an] &＃61; ∂det[a1, ..., ak-1, ak(1), ak&＃43;1, ... an] &＃43; ßdet[a1, ..., ak-1, ak(2),  ak&＃43;1, ... an]

2. 对于某个k&＃xff0c;有ak &＃61; ak&＃43;1那么有&＃xff0c;det[a1, ..., ak-1, ak&＃43;1, ... an] &＃61; det[a1, ..., ak, ak, ... an] &＃61; 0

3. 若令In &＃61; [e1, e2, ......, en] &＃61; [1, 0, ......, 0]

                                               [0, 1, ......., 0]

                                               [..................]

                                               [0, 0, ......, 1]

则有det In &＃61; 1

         给定m*n阶矩阵A&＃xff0c; 其P阶子式为一个p*p矩阵的行列式&＃xff0c;该p*p矩阵由矩阵A去掉m-p行&＃xff0c;去掉n-p列获得。其中p<&＃61;min{m, n}, [min{m,n}表示m和n中娇小的那个数]

         若矩阵A具有r阶子式&＃xff5c;M&＃xff5c;&＃xff0c;具备以下性质&＃xff1a;

1. &＃xff5c;M&＃xff5c;!&＃61; 0

2. 从A中再抽取一行和一列增加到M中&＃xff0c;由此得到的新子式为0&＃xff0c;有rank A &＃61; r; 因此&＃xff0c;矩阵A的秩等于他的非零子式最高阶数.

*一个非奇异(可逆)矩阵是一个行列式非0的方阵&＃xff0c;假定A为m*n方阵&＃xff0c;A为非奇异的&＃xff0c;当且仅当存在m*n的方阵B&＃xff0c;使得&＃xff1a;

            AB &＃61; BA &＃61; In &＃61;&＃61;&＃61;&＃61;> B &＃61; 1/A(逆矩阵)

*欧式内积&＃xff1a;x, y ∈ Rn,  &＃61; ∑i&＃61;1~n xiyi &＃61; x^Ty (此处^T为矩阵转置)

                     向量x的欧式范数(第二范数)||x|| &＃61; (x, x)^1/2 &＃61; (x^Tx)^1/2

*柯西施瓦茨不等式&＃xff1a;

        对于Rn中任意两个向量x, y&＃xff1b;|(x,y)| <&＃61; ||x|| ||y||

        柯西-施瓦茨不等式证明&＃xff1a;

            [证明]:先假定x, y为单位向量&＃xff0c;即||x|| &＃61; ||y|| &＃61; 1

                有0 <&＃61; ||x-y||^2 &＃61; &＃61; (x-y)(x-y)^T

                                            &＃61; ||x||^2 - 2 &＃43; ||y||^2

                                            &＃61; 2 - 2

                0 <&＃61; 2 - 2 &＃61;&＃61;&＃61;&＃61;>  <&＃61; 1 当且仅当x&＃61;y是等式成立.

*线性变换(定义)

        给定函数L: Rn -> Rm 若&＃xff1a;

            1. 对于任意x ∈ Rn, a ∈ R,都有L(ax) &＃61; aL(x);

            2. 对任意的x, y ∈ Rn&＃xff0c;都有L(x&＃43;y) &＃61; L(x) &＃43; L(y);

        则称函数L为一个线性变换

*特征值和特征向量

        A: n*n阶实数方阵&＃xff0c;存在标量 λ(可能为复数)和非零向量V满足等式AV &＃61; λV&＃xff0c;λ称为A的特征值&＃xff0c;V称为A的特征向量

         λ为A的特征值的充要条件&＃xff1a;矩阵λI - A是奇异的&＃xff0c;即det[λI - A] &＃61; 0&＃xff0c; I为n*n阶单位矩阵&＃xff0c;即有n次方程成立

                det[λI - A] &＃61; λ^n &＃43; an-1λ^n-1 &＃43; ...... a1λ &＃43; a0 &＃61; 0

        多项式det[λI - A]称为矩阵A的特征多项式&＃xff0c;而上面的方程称为特征方程(特征方程存在n个根&＃xff0c;即为A的n个特征值&＃xff0c;若A有n个相异的特征值&＃xff0c;那么他也有n个线性无关的特征向量)

*矩阵范数

        矩阵集合Rm*n可视为实数向量空间Rmn&＃xff0c;故矩阵向量范数向量同等于正则向量范数表记矩阵A的范数为||A||&＃xff0c;满足如下条件的任意函数||.||

1. 若A !&＃61; 0&＃xff0c;则有||A|| > 0, ||0|| &＃61; 0, 0为零矩阵

2. 对任意C ∈ R&＃xff0c;有||CA|| &＃61; |C| ||A||

3. ||A &＃43; B|| <&＃61; ||A|| &＃43; ||B||

4. ||AB|| &＃61; ||A|| ||B||

*Forbenius范数&＃xff1a;||A||F &＃61; (∑i&＃61;1~m∑j&＃61;1~n (aij)^2)^1/2 <&＃61;&＃61;&＃61;&＃61;>等价于Rmn上的欧式范数

矩阵范数与向量范数兼容&＃xff1a;||.||(n) : Rn和 ||.||(m) : Rm 为上的向量范数

任意矩阵A ∈ Rmn和任意向量x ∈ Rn存在如下不等式关系&＃xff1a;

                                ||Ax||(m) <&＃61; ||A|| ||x||(n)

则称该矩阵范数可由向量范数导出&＃xff0c;或者称其与向量范数兼容

*导出矩阵范数定义&＃xff1a;||A|| &＃61; max ||Ax||(m)

                                            ||x||(n)&＃61;1

            [||A||是向量Ax范数的最大值&＃xff0c;向量x是范数为1的任意向量]

*导数矩阵

        任意从Rn到Rm的线性变换&＃xff0c;特别是f:Rn -> Rm的导数L&＃xff0c;都可以表示为一个m*n的矩阵&＃xff0c;为了确认可微函数f:Rn -> Rm的导数L&＃xff0c;所对应的矩阵表示为l&＃xff0c;引入Rn空间的标准基&＃xff5c;e1, e2, ......, en&＃xff5c;考虑向量

            xj &＃61; x0 &＃43; tej&＃xff0c;j &＃61; 1, 2, ......, n

            根据导数定义&＃xff1a;lim(t->0) [f(xj) - (tlej &＃43; f(x0))]/t &＃61; 0

这表示&＃xff0c;对于j &＃61; 1, 2, ......, n 有&＃xff1a;

            lim(t->0) f(xj) - f(x0)/t &＃61; Iej

    [*Iej是矩阵I的第j列&＃xff0c;向量xj与x0仅仅在第j个元素上存在差异&＃xff0c;该元素上的差值为t]

        因此&＃xff0c;上式左侧等于偏导 ∂f/∂xj(x0)&＃xff0c;通过向量中每个元素求极限的方式来计算向量极限&＃xff0c;因此:

        f(x) &＃61; [f1(x)]

                   [.......]

                   [fm(x)]

---------->则有∂f(x)/∂xj(x0) &＃61; [∂f1/∂xj(x0)]

                                                      [.................]

                                                      [∂fm/∂xj(x0)]

上述矩阵可以写为&＃xff1a;

    [∂f/∂x1(x0) .......... ∂f/∂xn(x0)] &＃61; SHIFT NEXT

        [∂f1/∂x1(x0), ........., ∂f/∂xn(x0)]

        [.............................................]

        [∂fm/∂x1(x0), ......, ∂m/∂xn(x0)]

         matrix size : m*n]

*矩阵I称为f在点x0的雅可比矩阵或者导数矩阵&＃xff0c;记做Df(x0)&＃xff0c;方便起见&＃xff0c;常用Df(x0)表示f在点x0处的导数

*Hessian Matrix黑塞矩阵

        如果f: Rn -> R是可微的&＃xff0c;那么函数&＃xff1a;

                ▽f(x) &＃61; [∂f/∂x1(x)]

                             [...............]

                             [∂f/∂xn(x)]

                        &＃61;    Df(x)^T        称为f的梯度

        梯度是从Rn到Rm的函数&＃xff0c;如果绘制梯度向量▽f(x)&＃xff0c;其起点为点x&＃xff0c;箭头方向为梯度下降方向&＃xff0c;可将梯度表示为向量场

*给定函数f: Rn -> Rm&＃xff0c;如果梯度▽f可微&＃xff0c;则称f是二次可微的

         ▽f的导数记做&＃xff1a;

D^2f &＃61; [∂^2f/∂x1^2, ∂^2f/∂x2∂x1, .........., ∂^2f/∂xn∂x1]

           [∂^2f/∂x1∂x2, ∂^2f/∂x2^2, .........., ∂^2f/∂xn∂x2]

           [.....................................................................]

           [∂^2f/∂x1∂xn, ∂^2f/∂x2∂xn, .........., ∂^2f/∂xn^2]

        其中&＃xff0c;∂^2f/∂xi∂xj表示f先对xj求导&＃xff0c;再对xi求导的偏导数

**矩阵D^2f(x)称为f在点x的黑塞矩阵Hessian Matrix

*微分法则

        利用函数f: R -> Rn和函数g:Rn -> R可构成复合函数g(f(x))&＃xff0c;对其进行微粉时需要使用链式法则

        :如果g: D -> R在开集合D ⊂ Rn上是可微的&＃xff0c;且f:(a, b) -> D在(a,b)上可微&＃xff0c;复合函数h:(a,b) -> R, h(t) &＃61; g(f(x)) 在(a, b)上是可微的&＃xff0c;且导数为&＃xff1a;

        h&＃39;(t) &＃61; Dg(f(t))Df(t) &＃61; 

                ▽g(f(t))^T [f&＃39;(1)]

                                 [......]

                                 [fn&＃39;(t)]

*水平集和梯度特性

        函数f: Rn -> R在水平C上的水平集定义为

                    S &＃61; {x: f(x) &＃61; C}

        对于f: R2 -> R 水平集S是一条曲线(二维空间中)

        对于f: R3 -> R 水平集S是一组曲面(三维空间中)

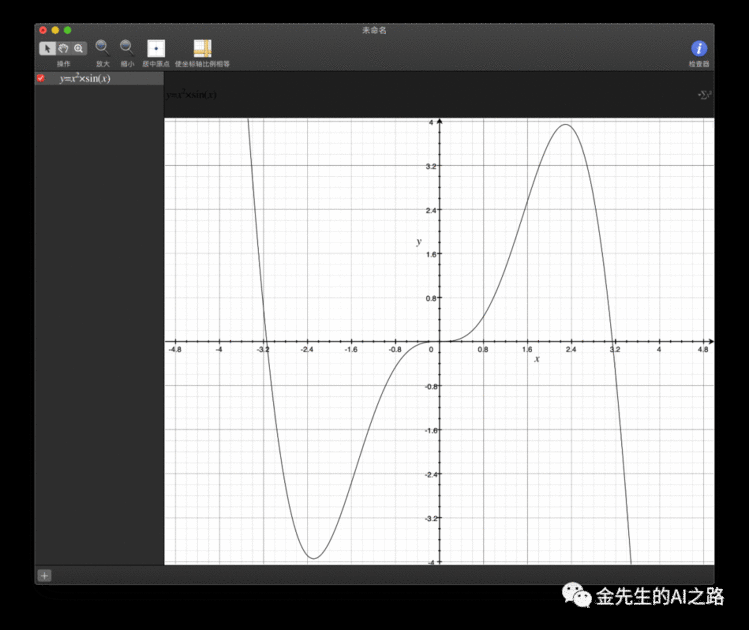
[以上图像绘制自MacBookPro Grapher简单二维曲线和RosenBrock香蕉函数]

*当提到点x0位于函数f的水平为C的水平集上时&＃xff0c;即&＃xff1a;f(x0) &＃61; C

        设存在一条位于S中的曲线γ,可以用一个连续的可微函数g:R-> Rn进行参数化&＃xff0c;同时设定g(t0) &＃61; x0且Dg(t0) &＃61; γ !&＃61; 0&＃xff0c;v为γ在x0点的切线向量

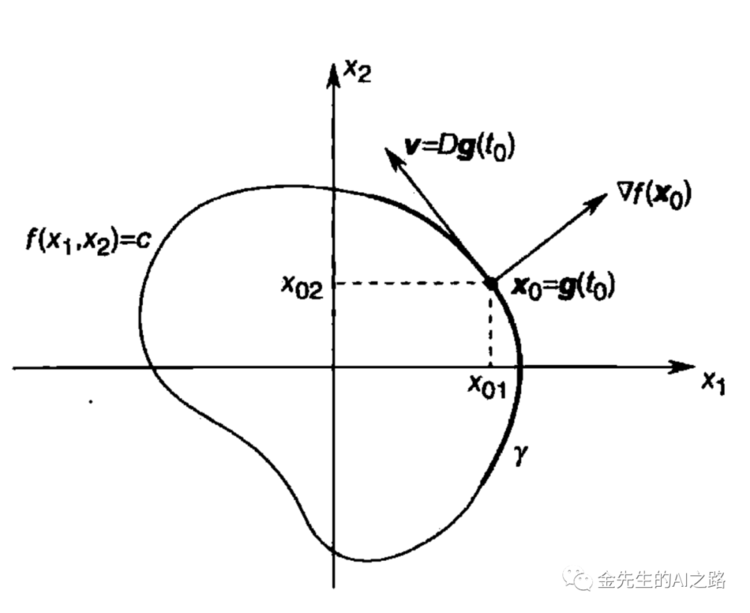
        *利用链式法则求解函数h(t) &＃61; f(g(t))/x0 在点t0上的导数

          h&＃39;(t0) &＃61; Df(g(t0))Dg(t0) &＃61; Df(x0)v

        γ存在于水平集S中。h(t) &＃61; f(g(t)) &＃61; C h为常数&＃xff0c;因此h&＃39;(t0) &＃61; 0且

Df(x0)v &＃61; ▽f(x0)^Tv &＃61; 0 (此处Df(x):导数矩阵or黑塞矩阵)

        *水平集和梯度的几大特征总结&＃xff1a;

          (1). :对于水平为f(x) &＃61; f(x0)的水平集中的任意一条经过点x0的光滑曲线其在点x0的切向量与函数f在点x0的梯度▽f(x0)正交(垂直)

          (2).▽f(x0)在点x0处正交于水平集S(或者可理解为▽f(x0)为在x0点外水平集S的法向量)

          (3).▽f(x0)为函数f在点x0处增加最快的方向&＃xff0c;一个实值可微函数在某点增加/缩小速度最快的方向正交于函数f在该点的水平集(此处的结论为日后神经网络等算法的梯度下降法提供了理论根据)

• 마지막으로 공식 보충(最后公式补充):

        가: 그레디언트(梯度公式)

        나 :자코비안(雅可比矩阵)

        다: 헤시안 행렬(黑塞矩阵)

参考文献&＃xff1a;An Introduction to Optimization (Fourth Edition)

인공지능 튜링 테스트에서 딥러닝까지생능출판 이건명 지음

end

AI技术交流 &＃43; 兴趣讨论&＃xff1a;