作者:以下犯上LOVE_845 | 来源:互联网 | 2024-11-14 19:31
蒜头君将两杯热水分别倒入两个杯子中,每杯水的初始量分别为a毫升和b毫升。为了使水冷却,蒜头君采用了一种特殊的方式,即每次将第一杯中的x%的水倒入第二杯,同时将第二杯中的y%的水倒入第一杯。这种操作会重复进行k次,最终求出两杯水中各自的水量。
问题描述
蒜头君将两杯热水分别倒入两个杯子中,第一杯中有a毫升,第二杯中有b毫升。由于水温过高,蒜头君决定通过交替倒水的方式来加速冷却。
每次倒水时,蒜头君会将第一杯中的x%的水倒入第二杯,同时将第二杯中的y%的水倒入第一杯。这个过程是同时进行的,没有先后顺序。
蒜头君会重复上述倒水操作k次,最终求出两杯水的容量。
输入格式
第1行包含两个正整数a和b(0 ≤ a, b ≤ 10^8),表示两杯水的初始容量。
第2行包含两个正整数x和y(0 ≤ x, y ≤ 100),表示每次倒水的比例。
第3行包含一个整数k(1 ≤ k ≤ 10^9),表示倒水的次数。
输出格式
输出两个浮点数,用空格隔开,分别表示第一杯水和第二杯水的最终容量(毫升)。输出结果的误差在10^-2以内均视为正确。
样例输入
样例输出
此问题可以通过矩阵快速幂来高效解决。首先,我们构建一个转移矩阵来表示每次倒水操作后的水量变化:
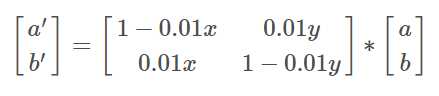
1 #include
2 using namespace std;
3 typedef long long LL;
4
5 struct matrix
6 {
7 double a[105][105];
8 };
9 matrix matrix_mul(matrix A, matrix B) // 矩阵A乘B
10 {
11 matrix C;
12 int i, j, k;
13 for(i = 0; i <= 1; i++)
14 {
15 for(j = 0; j <= 1; j++)
16 {
17 C.a[i][j] = 0;
18 for(k = 0; k <= 1; k++)
19 {
20 C.a[i][j] += A.a[i][k] * B.a[k][j];
21 }
22 }
23 }
24 return C;
25 }
26 matrix unit() // 单位矩阵
27 {
28 matrix res;
29 int i, j;
30 for(i = 0; i <= 1; i++)
31 {
32 for(j = 0; j <= 1; j++)
33 {
34 if(i == j)
35 res.a[i][j] = 1;
36 else
37 res.a[i][j] = 0;
38 }
39 }
40 return res;
41 }
42 matrix matrix_pow(matrix A, int n) // 矩阵快速幂
43 {
44 matrix res = unit(), temp = A;
45 for(; n; n /= 2)
46 {
47 if(n & 1)
48 res = matrix_mul(res, temp);
49 temp = matrix_mul(temp, temp);
50 }
51 return res;
52 }
53
54 int main()
55 {
56 double a, b, x, y, k;
57 scanf("%lf %lf %lf %lf %lf", &a, &b, &x, &y, &k);
58 matrix A, B, C;
59 // 转移矩阵
60 A.a[0][0] = 1 - x / 100; A.a[0][1] = y / 100;
61 A.a[1][0] = x / 100; A.a[1][1] = 1 - y / 100;
62 B.a[0][0] = a;
63 B.a[1][0] = b;
64 C = matrix_mul(matrix_pow(A, k), B);
65 printf("%.2lf %.2lf\n", C.a[0][0], C.a[1][0]);
66 return 0;
67 }
-
蒜头君的倒水问题(矩阵快速幂优化)