算法学习–广度优先搜索和深度优先搜索

广度优先搜索BFS

一、相关概念

1.图的遍历： 从图中某一顶点出发，按照某种搜索方法沿着图中的边对图中的所有节点访问一次且仅访问一次

二、算法流程

• 首先访问起始顶点 v ;


• 接着由出发依次访问 v 的各个未被访问过的邻接顶点 \(w_1,w_2,...,w_i\) ;


• 然后以此访问 \(w_1,w_2,...,w_i\) 的所有未被访问过的邻接顶点；


• 再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点；


• ......, 以此类推；

方法：队列 + 辅助标记数组（标记节点是否被访问过）

三、算法实现过程图示

• 初始化数组和队列，0表示为未被访问过

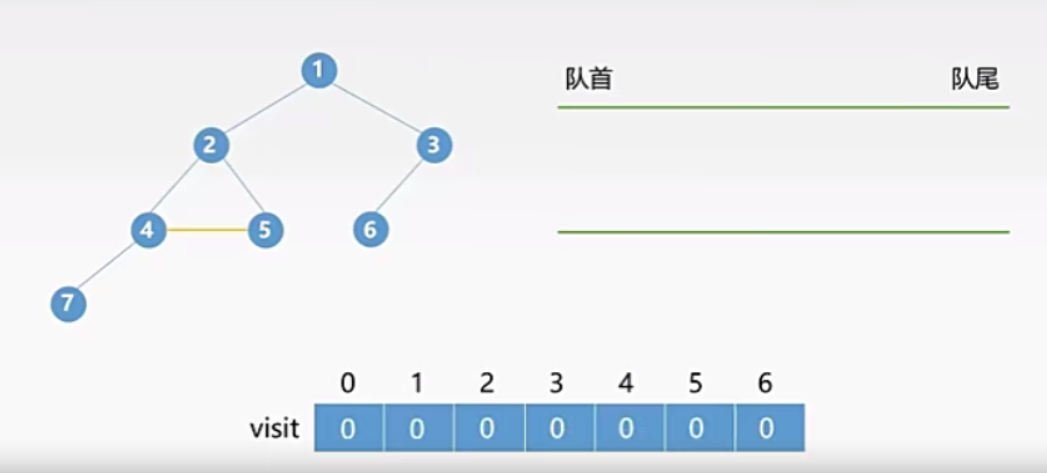
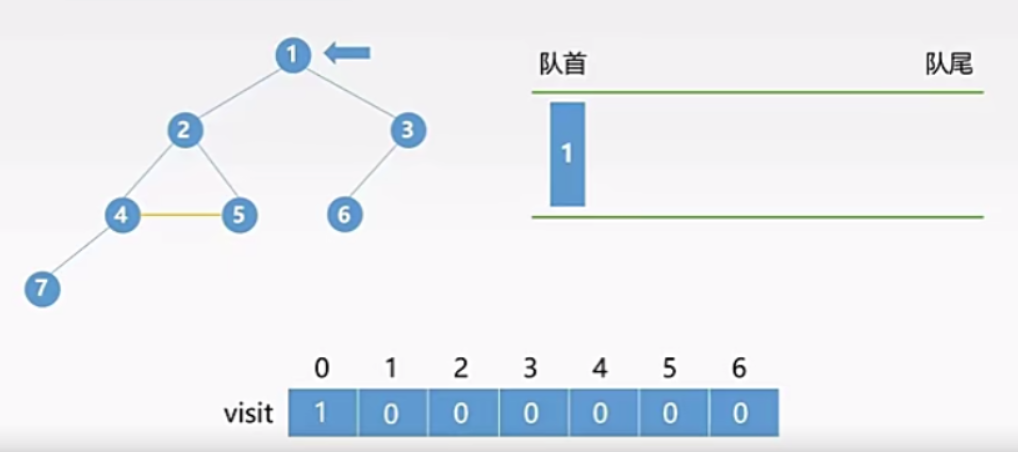
• 将结点 1 入队，并修改标记数组中对应的0位置的值为1(表示结点1已经被访问过)

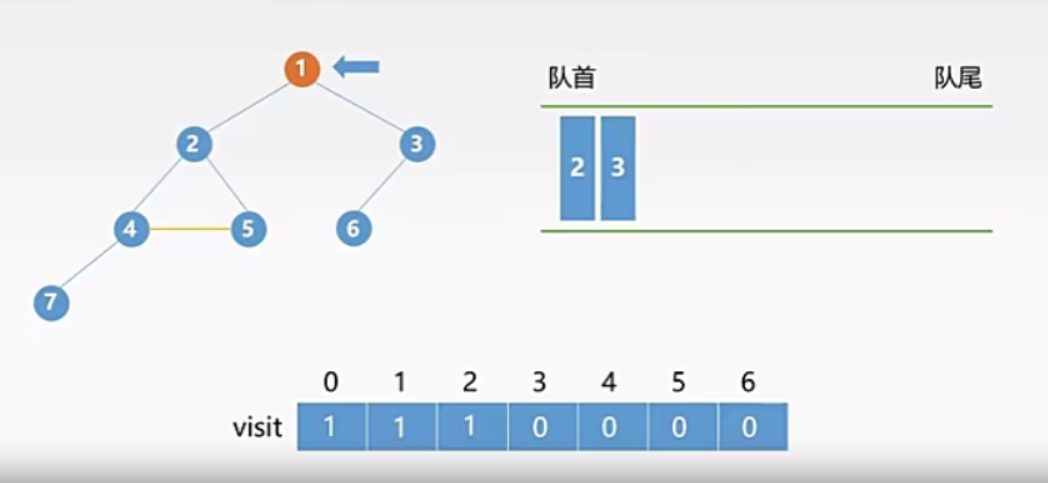
• 将队首元素 1 出队，并将它的所有未被访问的邻接结点(要求辅助标记为0)入队，并修改相应辅助数组下标的值

• 依次类推......

四、算法实现

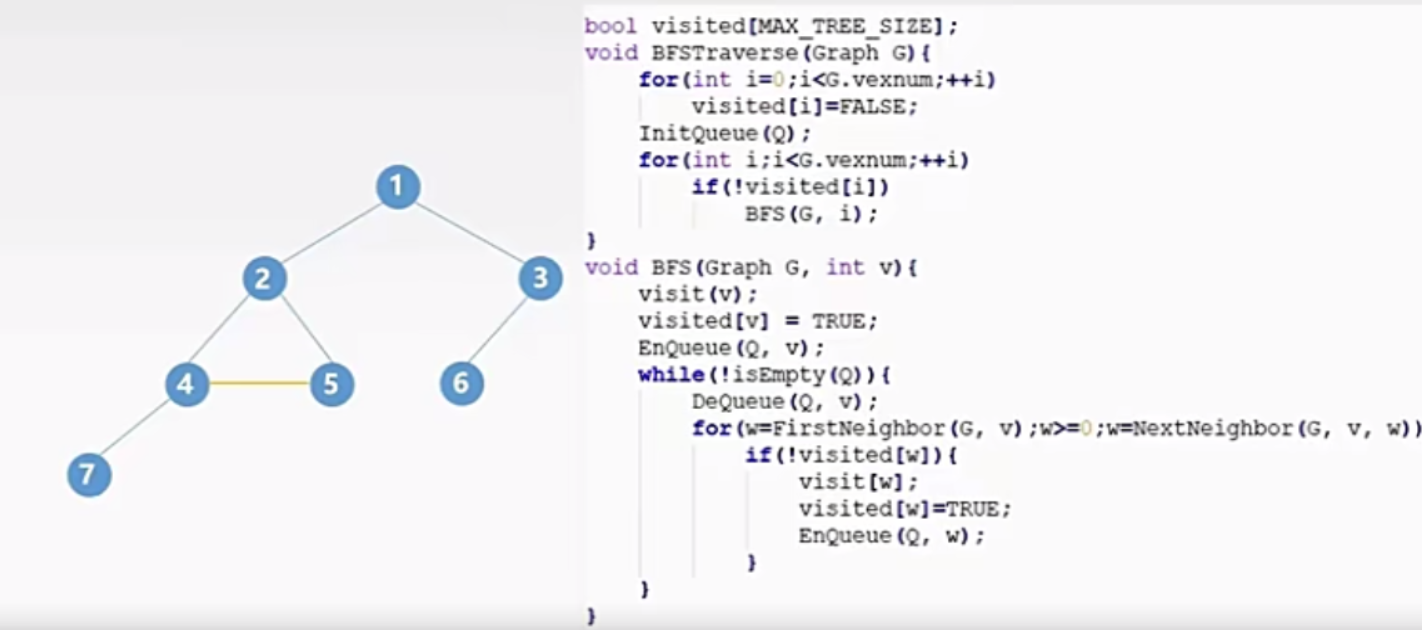
五、算法性能分析

• 空间复杂度： \(O(|V|)\) , 即顶点的数量大小（队列和辅助数组用到的空间大小都是顶点的数量大小）


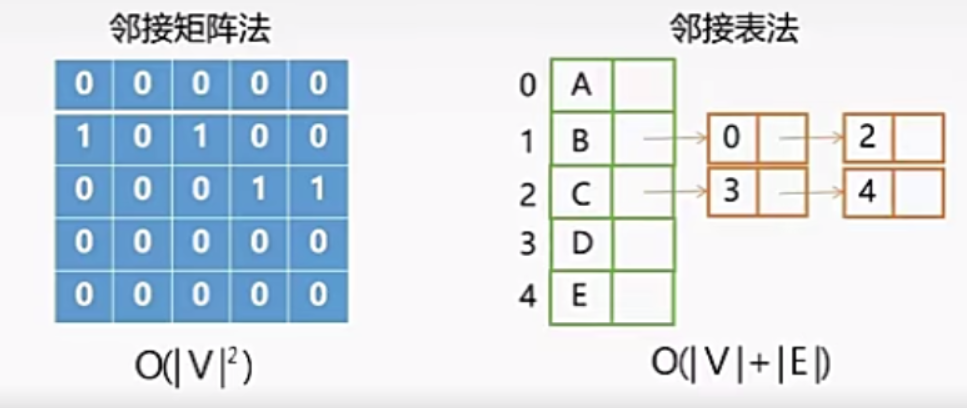
• 时间复杂度：取决于找邻接顶点的方法

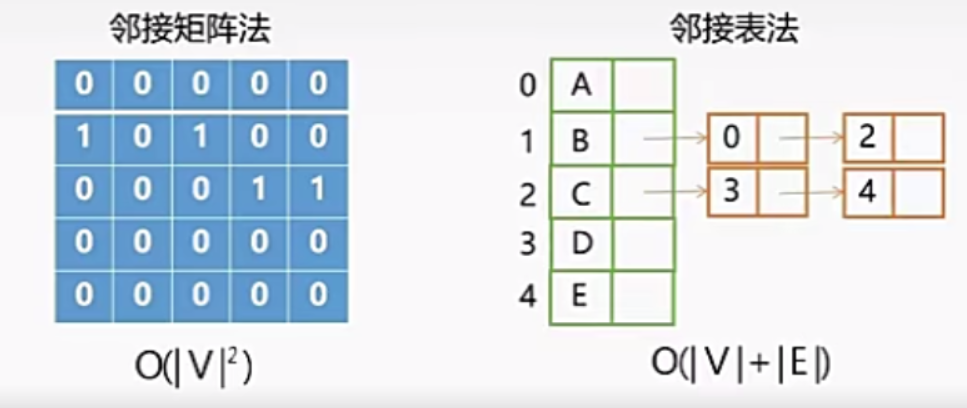
邻接矩阵法的DFS(BFS)序列唯一，邻接表法的不唯一

深度优先搜索DFS

一、算法流程

• 首先访问起始顶点 v ；


• 接着由 v 出发访问 v 的任意一个邻接且未被访问的邻接顶点 \(w_i\);


• 然后再访问与 \(w_i\) 邻接且未被访问过的任意顶点 \(y_i\);


• 若 \(w_i\) 没有邻接且未被访问的顶点时，就退回到它的上一层顶点 v ;


• 重复上诉过程，知道所有的顶点被访问完为止。

方法：栈 + 辅助标记数组

二、算法实现

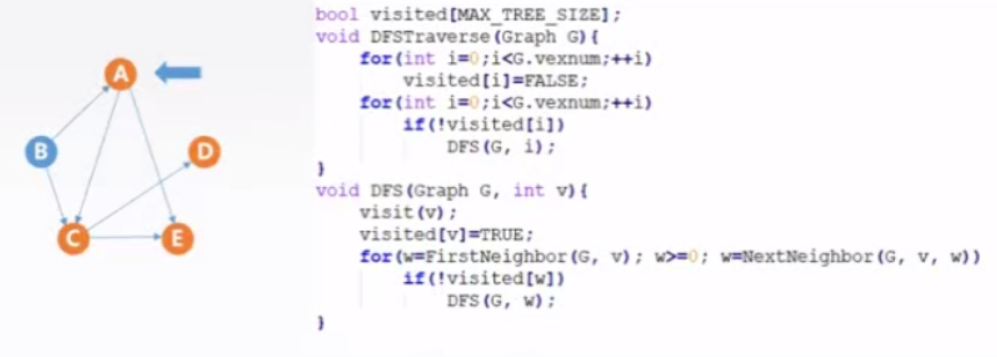
三、算法性能分析

• 空间复杂度： \(O(|V|)\) , 即顶点的数量大小（工作栈和辅助数组用到的空间大小都是顶点的数量大小）


• 时间复杂度： 根据找邻接结点的方式而定

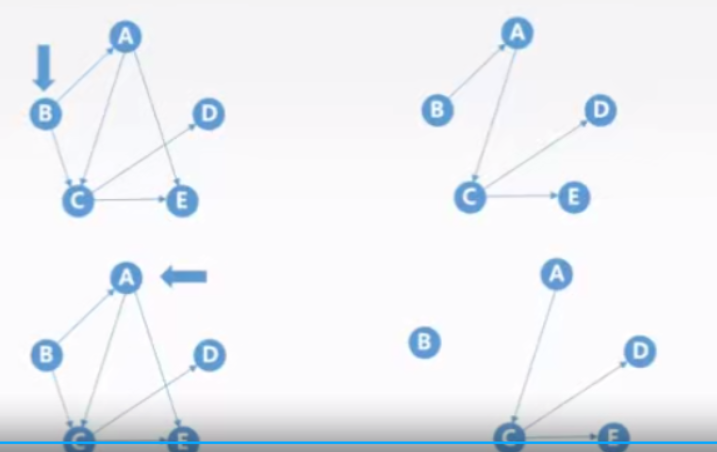
四、如何通过遍历来判断连通性

• 在无向图当中，在任意结点出发进行一次遍历 (调用一次BFS或者DFS)，若能访问全部结点，说明该无向图是连通的；


• 在无向图中，调用遍历函数(BFS或者DFS) 的次数为连通分量的个数；


• 针对有向图，上述结论不成立：因为有向图是有方向的，从一个顶点出发不一定能返回来，但是无向图可以。