串的模式匹配也称为子串的定位操作,即查找子串在主串中出现的位置。它是经常用到的一个算法,也是数据结构中的一个难点之一。串的模式匹配算法常见的有两种:Brute-Force朴素模式匹配算法和KMP算法。
【Brute-Force算法】
子串的定位操作串通常称为模式匹配,是各种串处理系统中最重要的操作之一。设有主串S和子串T,如果在主串S中找到一个与子串T相等的串,则返回T的第一个字符在串S中的位置。其中,主串S又称为目标串,子串T又称为模式串。
Brute-Force算法的思想是:从主串S=“s0s1s2…sn-1”的第pos个字符开始与模式串T=“t0t1t2…tm-1”的第一个字符进行比较,如果相等则继续逐个比较后续字符;否则从主串的下一个字符开始重新与模式串T的第一个字符进行比较,依此类推。如果在主串S中存在与模式串T相等的连续字符序列,则匹配成功,函数返回模式串T中第一个字符在主串S中的位置;否则返回-1表示匹配失败。
假设主串S=”ababcabcacbab”模式串T=”abcac”,S的长度n=13,T的长度m=5。用变量i表示主串S当前正在比较字符的下标,变量j表示子串T中当前正在比较字符的下标。模式匹配的过程如图
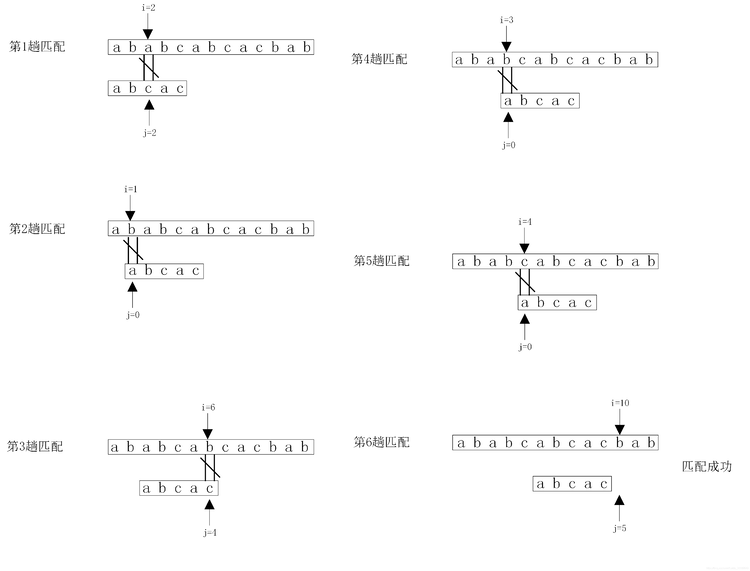
【BMP算法】
KMP算法是由D.E.Knuth、J.H.Morris、V.R.Pratt共同提出的,因此被称为KMP算法(Knuth-Morris-Pratt算法)。KMP算法在Brute-Force算法的基础上有较大的改进,可在O(n+m)时间数量级上完成串的模式匹配,主要是消除了主串指针的回退,使算法效率有了很大的程度的提高。
根据Brute-Force算法,遇到不相等的字符,将子串后移一位,再从头逐个比较。这样做虽然可行,但是效果很差,因为你要将主串和子串的指针都退回到原来的位置,将已经比较过的字符重新比较一遍。
KMP算法思想是:在每一趟匹配过程中出现字符不等时,不需要回退主串的指针,而是利用已经得到前面“部分匹配”的结果,将模式串向右滑动若干个字符后,继续与主串中的当前字符进行比较。
假设主串S=”ababcabcacbab”模式串T=”abcac”。KMP算法匹配过程如图
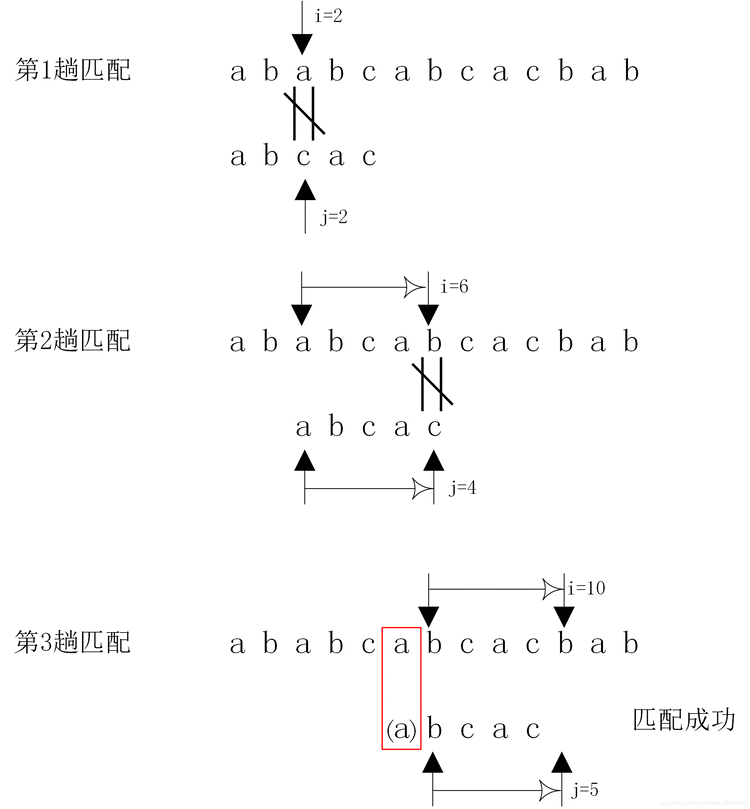
从图中可以看出,KMP算法的匹配次数从原来的6趟减少为3趟。而对于Brute-Force算法,在第3趟匹配过程中,当i=6,j=4时,主串中的字符与模式串中的字符不相等,又从i=3,j=0开始比较。经过仔细观察,其实在i=3,j=0,i=4,j=0,i=5,j=0这三次比较过程都是没有必要的。因为从第3趟的部分匹配课得出:S2=T0=’a’,S3=T1=’b’,S4=T2=’c’,S5=T3=’a’,S6≠T4,因为S3=T1且T0≠T1,所以S3≠T0,所以没有必要从i=3、j=0开始比较。又因为S4=T2,且T0≠T2,故S4≠T0,所以S4与T0也没有必要从i=4、j=0开始比较。又因为S5=T3且T0=T4,故S5=T0,所以也没有必要将S5与T0进行比较。
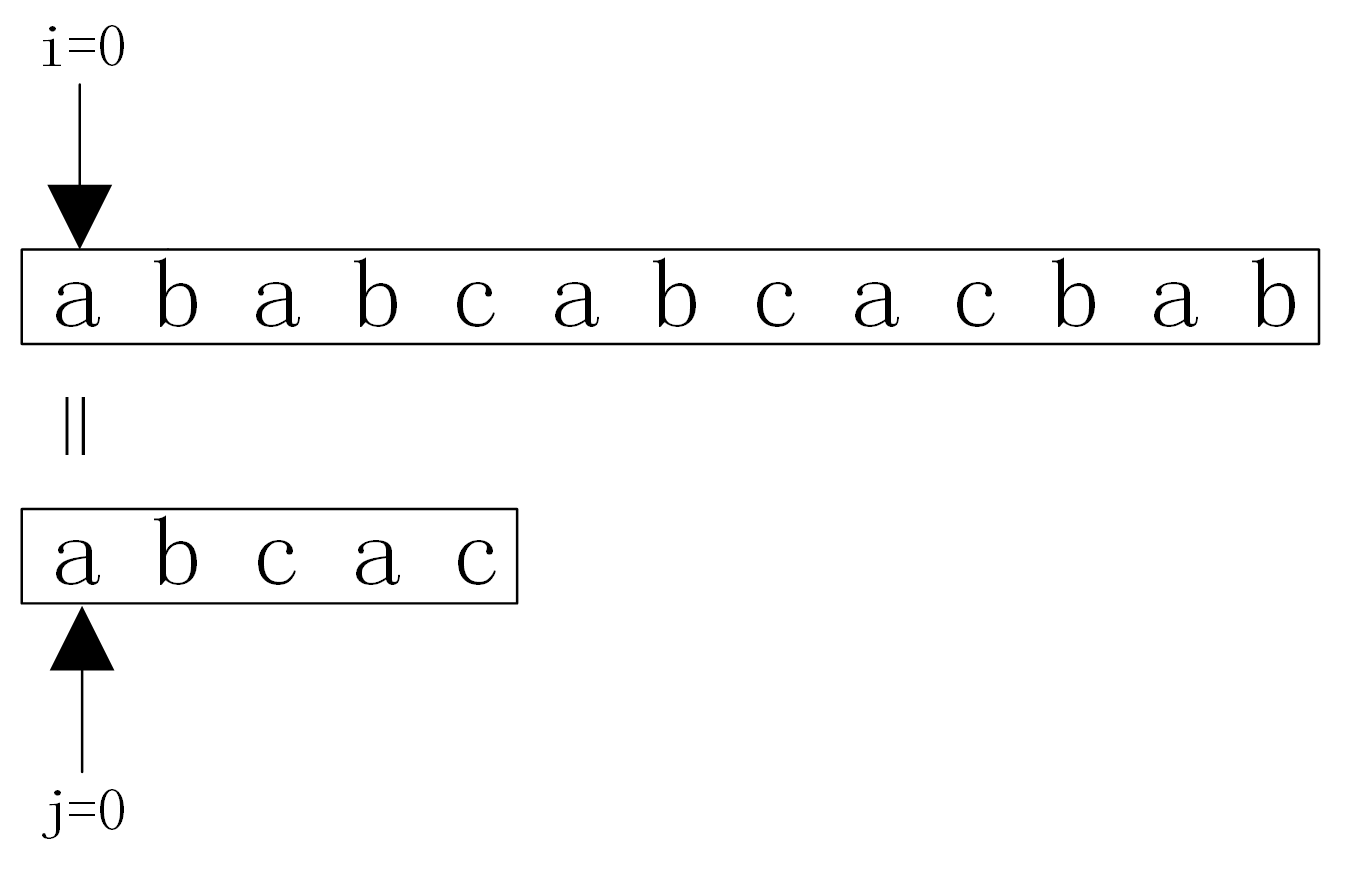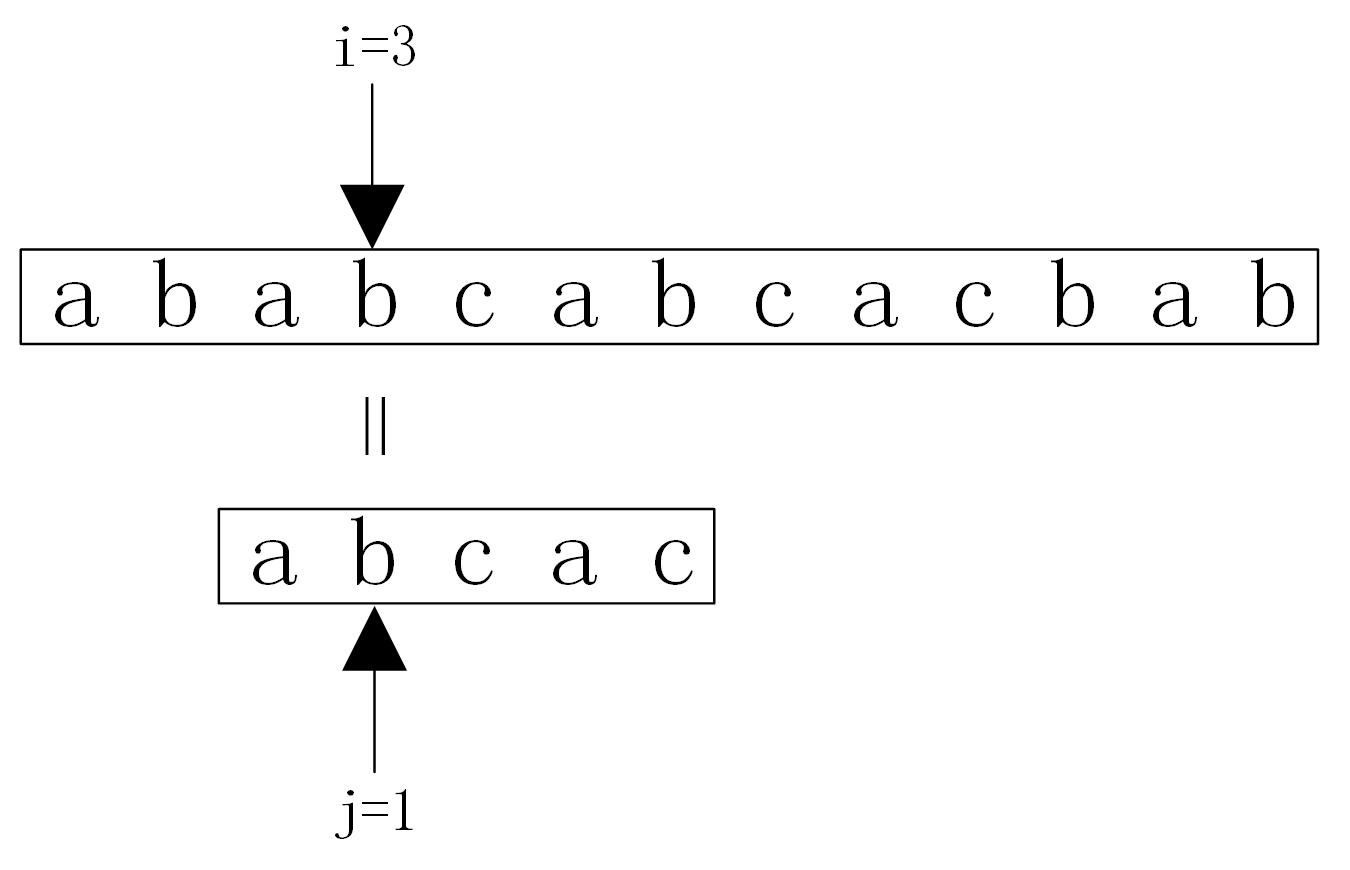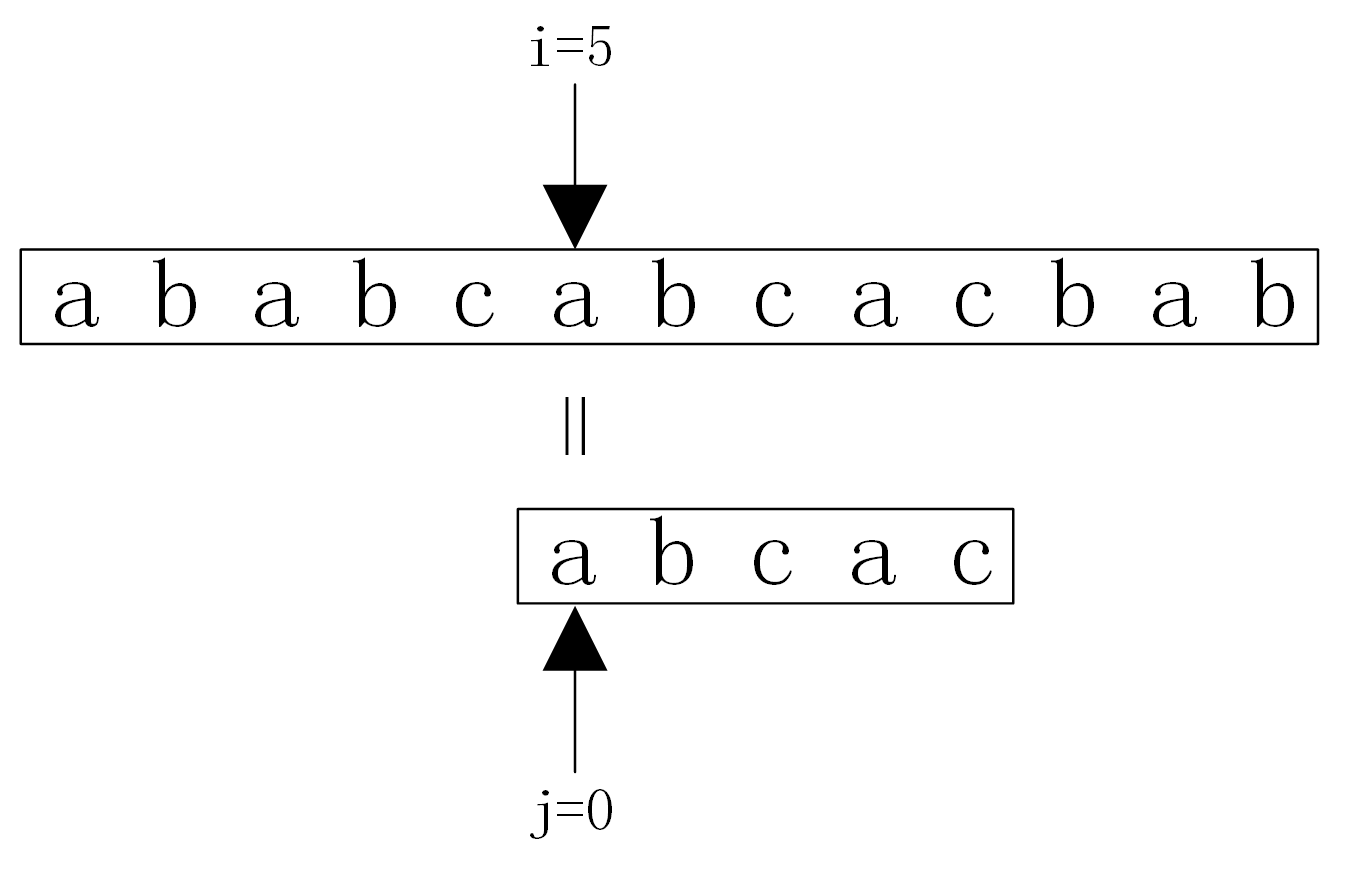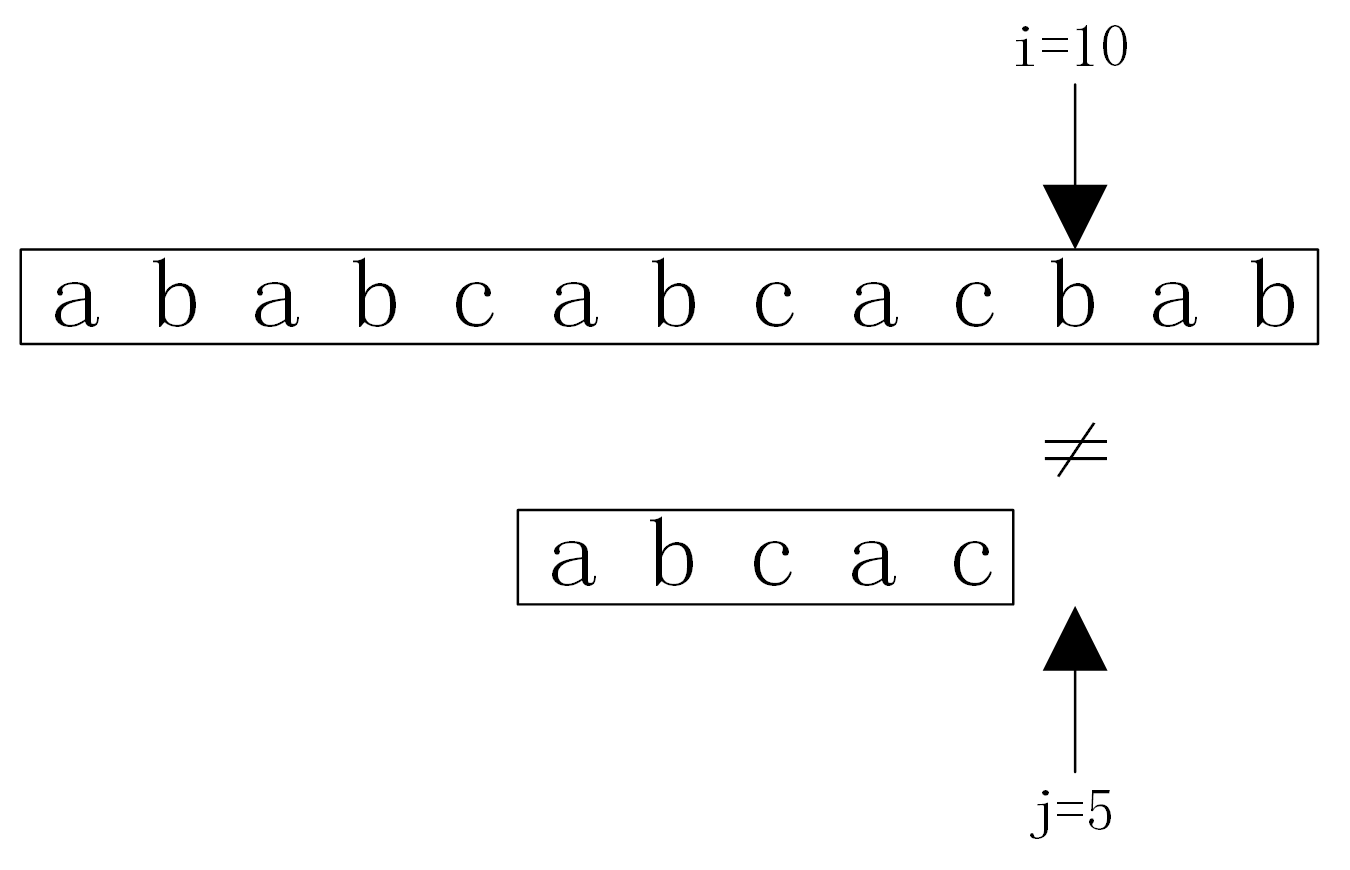
也就是说,根据第3趟的部分匹配也可以得出结论:Brute-Force算法算法的第4、5趟是没有必要的,第6趟也没有必要将主串的第6个字符与模式串的第1个字符比较。

因此,只需要将模式串向右滑动3个字节,从i=6,j=1开始比较。同理,在第1 趟匹配的过程中,当出现字符不相等时,只需将模式串向右滑动2个字符,从i=2、j=0开始比较即可。在整个KMP算法中,主串中的i指针没有回退。 “si-j si-j+1 … si-1″=”tj-k tj-k+1 … tj-1″(1) 即说明至少在字符si之前有一部分字符是相等的。 若子串(即模式串)中存在收尾重叠的真子串,即: “t0 t1 … tk-1” = “tj-k tj-k+1 … tk-1″(2) 根据(1)(2)可以得出: “si-k si-k+1 … si-1” = “t0 t1 …tk-1” 如图 因此,在匹配的过程中,主串中的第i个字符与模式串的第j个字符不等时,仅需将子串向右滑动,使si与tk对齐,接着进行后续的比较,此时,模式串中的子串”t0 t1 … tk-1″ 必与主串中的子串”si-k si-k+1 … si-1″ 相等。 如图 【求next函数值】 下面就来确定模式串需要滑动的具体位置。令next[j]=k,则next[j]表示当模式串中的第j个字符与主串中对应的字符不相等时,需要重新与主串比较的模式串字符位置,也就是需要将模式串滑动到第几个字符与主串比较。 求模式串中的next函数定义如下图: 其中,第1种情况,next[j]的函数是为了方便算法设计而定义的; 由此可以得到模式串“abcac”的next函数值 如图 KMP算法的模式匹配过程:如果模式串T中存在真子串”t0 t1 … tk-1″ = “tj-k tj-k+1 … tj-1″,当模式串T的tj与主串的si不相等,按照next[j]=k将模式串向右滑动,从主串中的si与模式串的tk开始比较。如果si=tk,则继续比较下一字符。如果si≠tk,则按照next[next[j]]将模式串继续向右滑动,将主串中的si与模式串中的next[next[j]]字符进行比较。如仍然不相等,则按照以上方法,将模式串继续向右滑动,直到next[j]=-1为止。这时,模式串不再向右滑动,从si+1开始与t0进行比较。 利用next函数值的一个模式匹配例子 如图 KMP模式匹配算法是建立在模式串的next函数值已知的基础上的。下面讨论如何求模式串的next函数值。 从上面的分析可以看出,模式串的next函数值的取值与主串无关,仅与模式串相关。根据模式串next函数定义,next函数可以由地推的方法得到。 设next[j]=k,表示在模式串T中存在以下关系: “t0 t1 … tk-1” = “tj-k tj-k+1 … tj-1” 其中,0 (1)若tj=tk,则表示在模式串T中满足以下关系: (2)若tj≠tk,则表示模式串T中满足以下关系: “t0 t1 … tk” ≠ “tj-k tj-k+1 … tj” 此时,已经有”t0 t1 … tk-1″ = “tj-k tj-k+1 … tj-1″,但是tj≠tk,把模式串T向右滑动到k’=next[k](0 因此得到 next[j+1]=k’+1 即next[j+1]=next[k’]+1 如果tj≠tk’ ,则将模式串继续向右移动到next[k’]个字符与tj比较。如果仍不相等,则将模式串继续向右滑动到下标为next[next[k’]]字符与tj进行比较。依此类推,直到tj和模式串中某个字符相等或者不存在任何k’满足”t0 t1 … tk’ ” = “tj-k tj-k+1 … tj”,则有 next[j+1]=0 上述讨论的是根据next函数的定义如何得到next函数值的方法。例如,模式串为T=”abcdabcdabe”的next函数值 如图 例如,在已经得到的前3个字符next函数值的基础上,如果求next[3]。因为next[2]=1,且t2=t0,则next[3]=next[2]+1=2。接着求next[4],因为t2=t0,但“t2t3”≠“t0t1”,所以需要将t3与下标为next[1]=0的字符即t0进行比较,因为t0≠t3,所以next[4]=1。
下面来讨论一般情况。设主串S=“s0s1s2…sn-1”模式串T=“t0t1t2…tm-1”。在模式匹配过程中,若出现字符不匹配的情况,即当si≠tj(0≤i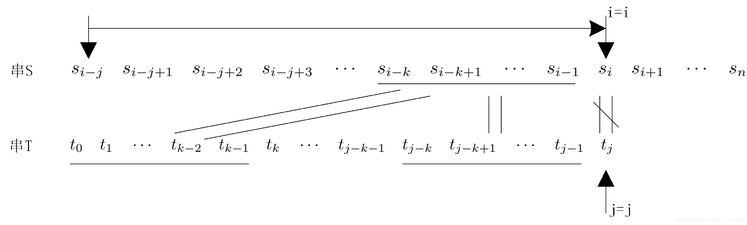
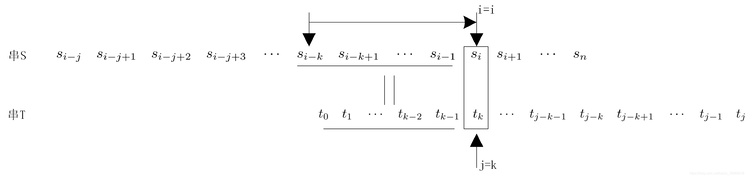
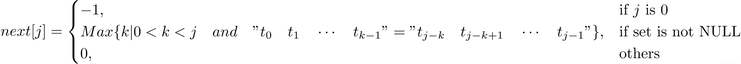
第2种情况,如果子串(模式串)中存在首尾重叠的真子串,则next[j]的值就是k,即模式串的最长子串的长度;
第3种情况,如果模式串中不存在重叠的子串,则从子串的第一个字符开始比较。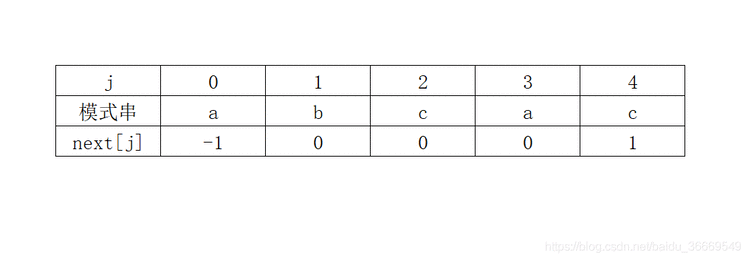
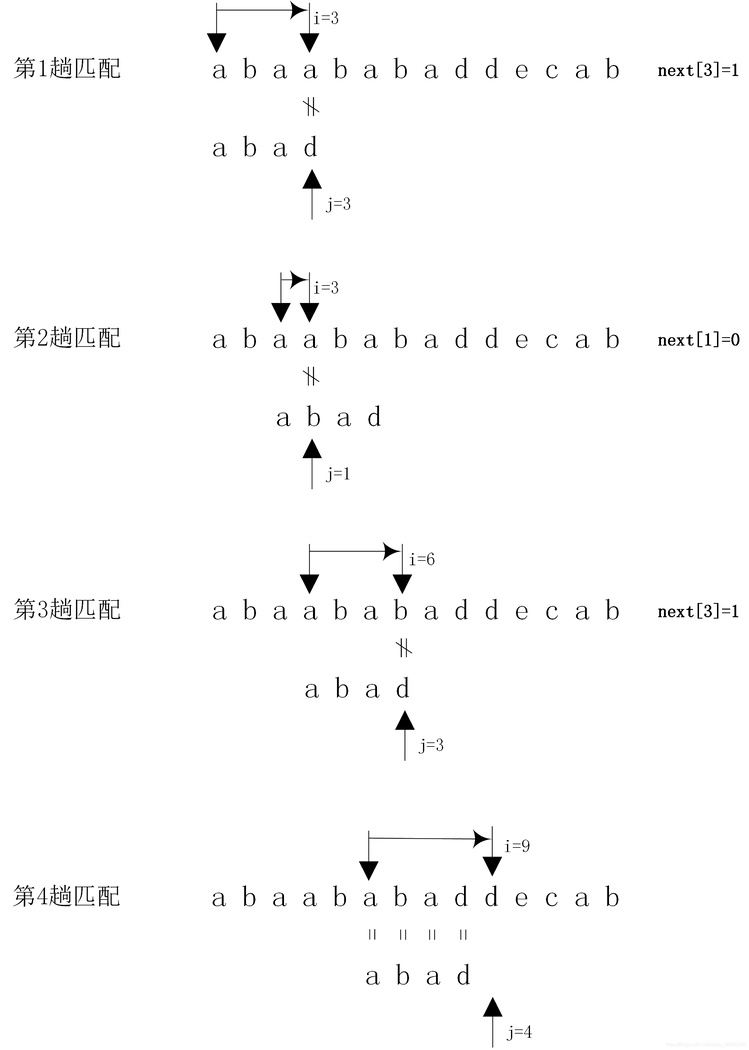
“t0 t1 … tk” = “tj-k tj-k+1 … tj”
并且不可能存在k’>k满足以上等式。因此有
next[j+1]=k+1,即next[j+1]=next[j]+1

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有