一、Matlab简介•Matlab名字是由Matrix和Laboratory两个词的前三个字母组合而成的,是由MathWorks公司于1982年推出的一套高性能的数值计算和可视化
一、Matlab 简介
• Matlab名字是由Matrix和Laboratory两个词的前三个字母组合而成的,是由MathWorks公司于1982年推出的一套高性能的数值计算和可视化数学软件。
• Matlab编程运算与人进行科学计算的思路和表达方式完全一致。不像学习其它高级语言如Basic、Fortran和C等那样难于掌握。
• 其基本元素是矩阵 。
• 具有强大的数值计算和图示能力。
• 具有丰富的工具箱(ToolBox)。
• 在高校中,Matlab已成为数学,信息,控制等诸多学科有关课程的有效教学工具。
二、Matlab 的安装与启动
下载安装自行百度即可;
附一个更改Matlab默认保存文件路径的方法,R2015b实测有效:
https://blog.csdn.net/u012210613/article/details/52346842
三、Matlab 编程基础
• 1 变量
变量无需定义即可使用。
变量名的大小写是敏感的。
变量的第一个字符必须为英文字母,而且不超过31个字符。
变量名可以包含下连字符、数字,但不能为空格符、标点 。
• 2 数组,向量与矩阵的创建和访问
• 在Matlab中,这三个概念在创建和显示的时候没有任何区别。
• 向量的创建 要创建一个向量,在命令窗口下输入:
t=0:1:10
屏幕显示:
t =
0 1 2 3 4 5 6 7 8 9 10
注意:
向量的第一个元素的下标是1,而不是0。
T=0:1:10产生了0~10步长为1的共11个数,保存在t(1),t(2), ┉t(11)中。
• 矩阵的创建
例如:创建一个3×3的矩阵,输入 :
a=[1 2 3;4 5 6;7 8 9]
屏幕输出
a =
1 2 3
4 5 6
7 8 9
• 访问矩阵的某一个元素:
a(3,2)
ans=
8
访问矩阵某行(列)的所有元素:
a(3,:) a(:,2)
注意:这两个符号分别是1*3行向量和3*1列向量
• 3 部分特殊变量和常数
• ans 最近生成的无名结果
• eps 浮点数的相对误差
• pi 圆周率(3.1415926)
• i 虚数单位
• j 虚数单位
• inf 无穷大,如n/0
• 4 部分常用运算符
1 算术运算符
• + 加
• - 减
• * 乘(包括标量乘,矩阵乘,标量与矩阵乘)
• / 除(包括标量除,矩阵除标量,数组除标量)
• ^ 矩阵求幂(矩阵必须为方阵)
• .* 数组相乘
• ./ 数组相除
• .^ 数组求幂
注意:.* ./ 表示两个同维数组中的对应元素做乘,除;. ^ 表示对数组的每个元素求幂
2 关系运算符
• <小于
• <= 小于等于
• > 大于
• >= 大于等于
• == 等于
• ~= 不等于
运算法则:若关系式成立,结果为1;若关系式不成立,结果为0
3 逻辑运算符
• & 与
• | 或
• ~ 非
运算法则: 若逻辑真,结果为1;若逻辑假,结果为0。
4 其他常见符号
• = 变量赋值
• % 注释符
• ‘ 共轭转置符
• : 冒号运算符
• n:s:m 产生n~m,步长为s的序列,s可以为
正或负或者小数,默认值为1。
• 5 Matlab的程序设计
• Matlab的工作方式有二种
1. 交互式的指令操作方式。即用户在命令窗口中输入命令并按下回车键后,系统执行该指令并立即
给出运算结果。
2. m文件的编程方式。m文件是由 matlab语句构成的文件,且文件名必须以.m为扩展名,如example.m。用户可以用任何文件编辑器来对M文件进行编辑。
• 顺序结构:
Matlab 从上到下依次执行各语句,该结构最简单。
• 循环结构
(1)for-end 循环
用于循环次数事先确定的,格式为
for i=n:s:m
语句体
end
s 为步长,可以为正数,负数或小数。
(2)while-end 循环
用于循环次数不能事先确定的,格式为
while 表达式
语句 体
end
只有表达式为真,就执行语句体,表达
式为假,终止该循环。
• 分支结构
• (1) if 语句
格式为
if 表达式1
语句体1
elseif 表达式2
语句体2
………..
else
语句体
end
• 6 m文件的创建,保存
• 创建
【File】菜单下【New】菜单选项的【M-File】命 令 打开matlab的m文件编辑器窗口 。
• 保存
单击M文件编辑器窗口工具栏中的【 Save】图标,打开保存对话框
• 7 基本数学函数和基本绘图函数
sin(x) cos(x) tan(x) cot(x) exp(x)
log(x) :自然对数
log10(x): 以10为底的对数
log2(x):以2为底的对数
abs(x):取模
conj(x):取共轭
real(x):取实部
imag(x):取虚部
• Matlab提供了强大的图形绘制功能。
在大多数情况下,用户只需要指定绘图的方式,提供绘图数据,利用Matlab提供的丰富的二维,三维图形函数,就可以绘制出所需的图形。
• 1 .绘制二维连续函数
Matlab中最常用的绘图函数是plot,plot的命令格式有以下几种:
• (1) plot(y)
当y为一向量时,以y的序号作为x轴,按向量y的值绘制曲线。
• (2) plot(x,y)
x,y均为向量时,以x向量作为X轴,向量y作为Y轴绘制曲线。
注意:x和y种元素的个数必须相同!
在Matlab用stem命令实现离散序列的绘制。
stem命令的格式有以下几种:
(1)stem(y)
以x=1,2,3……为各点数据的x坐标,以y向量的各个对应元素为y坐标,在(X,Y)坐标面画一个空心小圆圈。
(2)stem(x,y,’filled’)
以x向量的各个元素为x坐标,以y向量的各个对应元素为y坐标,在(X,Y)坐标面画一个实心小圆圈,并连接一条线段到X轴。
• 8 编程举例
例一.用图形表示连续调制波形y=sin(t)sin(9t)及其包络。
程序如下:
t=(0:pi/100:pi)’;% 长度为101 的时间采样列向量
y1=sin(t)*[1,-1];% 包络线函数值,是(101x2 )的矩阵
y2=sin(t).*sin(9*t); % 长度为101 的调制波列向量
t3=pi*(0:9)/9;
y3=sin(t3).*sin(9*t3);
plot(t,y1,&#39;r:&#39;,t,y2,&#39;b&#39;,t3,y3,&#39;bo&#39;)
axis([0,pi,-1,1]) %控制轴的范围
运行结果:

四、Matlab 在数字信号处理课程中的应用
• 常见连续信号
• 周期信号:正弦信号,周期方波
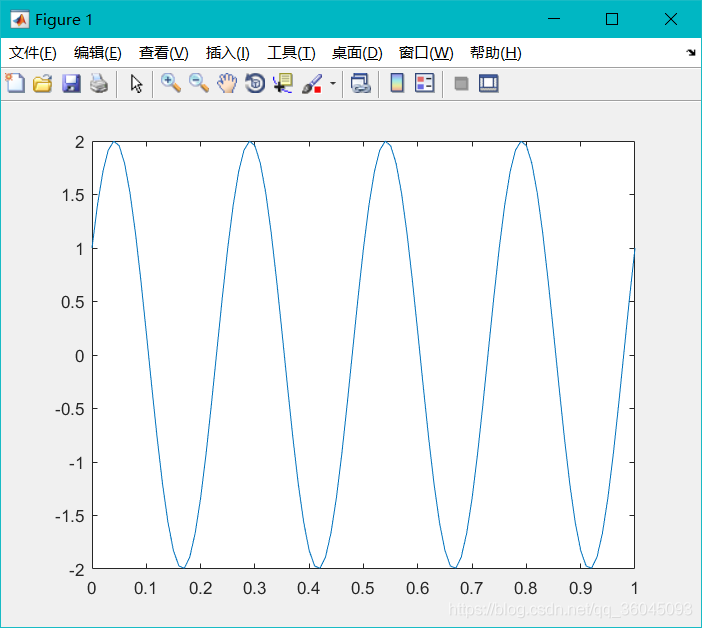
例二 产生一个幅度为2,频率为4Hz,相位为π/6的正弦信号
A=2;% 振幅
f=4;% 频率
phi=pi/6;% 初相位
w0=2*pi*f;% 角频率
t=0:0.01:1;% 描点
x=A*sin(w0*t+phi);% x取值
plot(t,x);
运行结果:
• 非周期信号:指数信号,阶跃信号,取样函数Sa(x)等
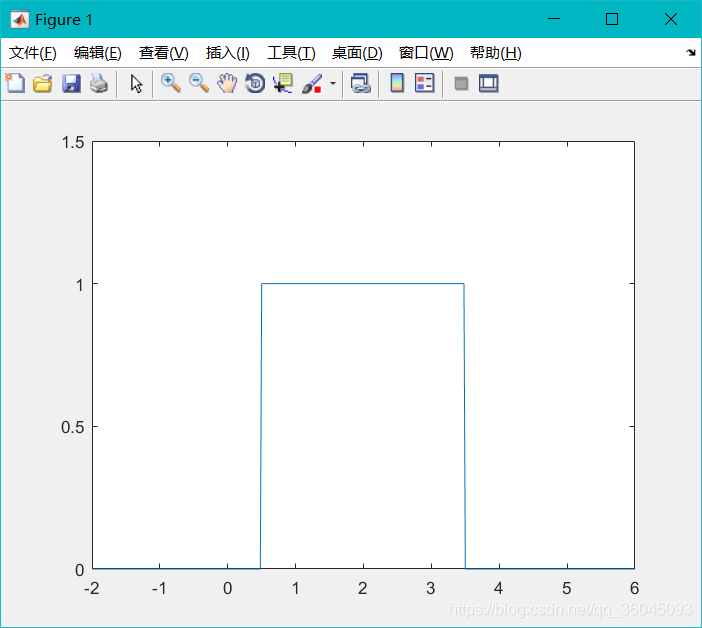
例三 产生一个高度为1,宽度为3,延时为2秒的矩形脉冲信号
t=-2:0.02:6;% 自变量取值范围
plot(t,rectpuls(t-2,3));
% rectpuls(t,width)用以产生一个幅值为1,宽度为width,
% 相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,
% 是以t=0为中心向左右各展开width/2的范围,width的默认值为1。
% t-2根据“左加右减”,即对称轴为x=2
axis([-2,6,0,1.5]);
运行结果:
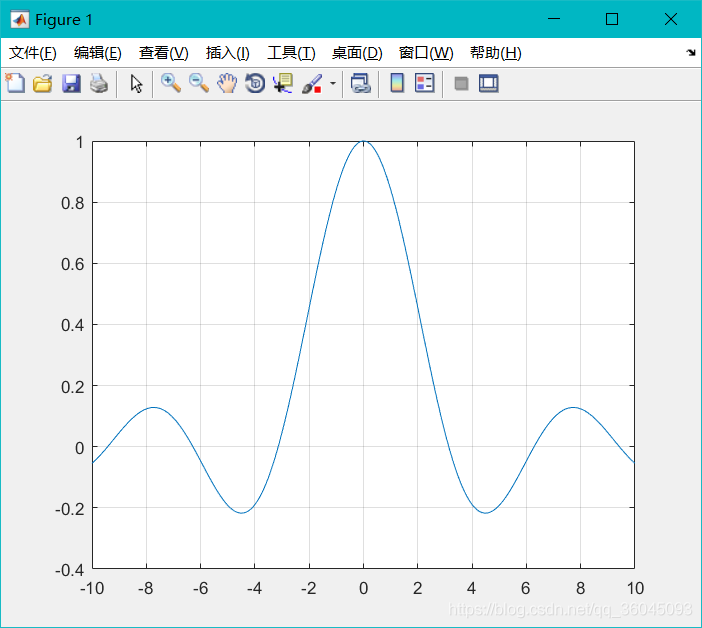
例四 取样函数:用sinc(x)命令
N=1000;
t=-10:20/N:10;
x=sinc(t/pi);
plot(t,x);
grid on
运行结果:
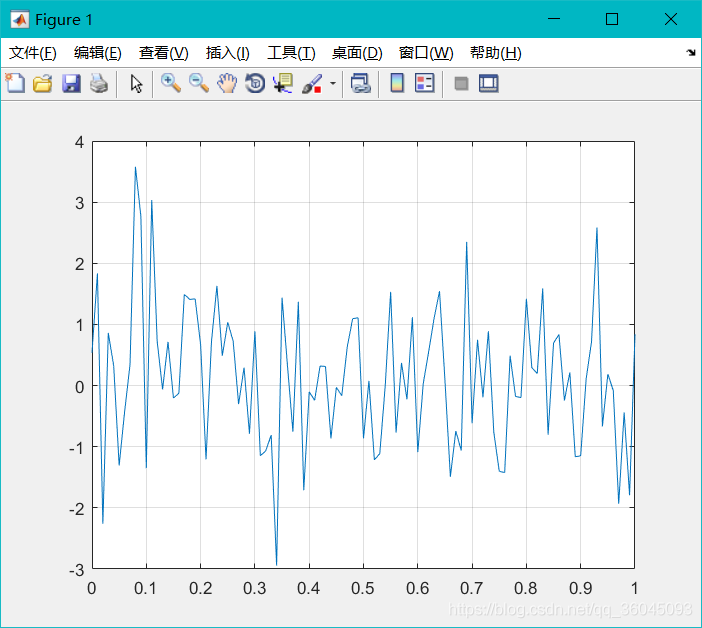
• 随机信号:
rand产生均匀分布的白噪声,randn产生高斯分布的白噪声
t=0:0.01:1;
y=randn(1,length(t));
plot(t,y);grid on;
运行结果:
• 离散信号
• 周期序列
例五 产生一个幅度为2,频率为4Hz,相位为π/6的正弦信号
A=2;% 幅值
phi=pi/6;% 初相位
omega=2*pi/12;% 角频率
n=-10:10;% 自变量范围:21个点
x=A*sin(omega*n+phi);
stem(n,x,&#39;fill&#39;);% 描实心点
grid on;% 打开网格
运行结果:
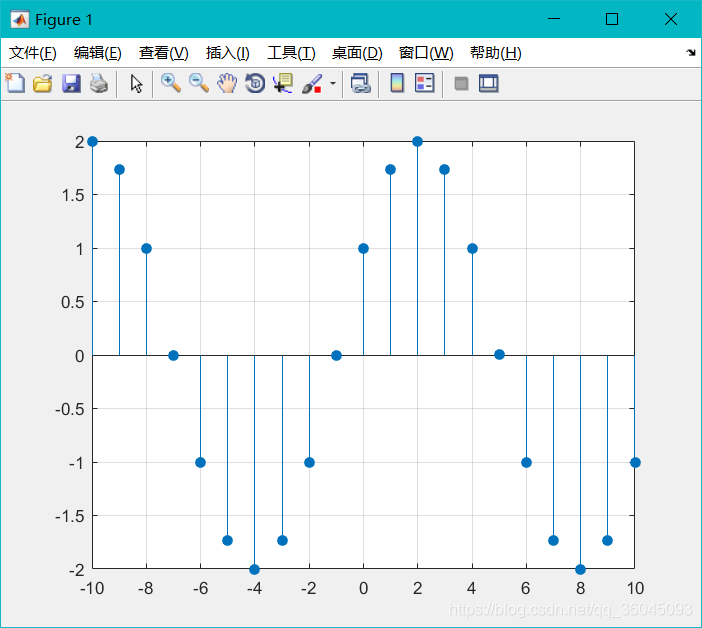
例六 产生单位脉冲序列δ[n]和单位阶跃序列u[n-3]
• 单位脉冲序列δ[n]和单位阶跃序列u[n]可以用ones(1,n)和zeros(1,n)来生成单位脉冲序列和单位阶跃序列
ones(1,n)命令产生1行n列的1值
zeros(1,n)命令产生1行n列的0值
n=-5:30;
x=[zeros(1,8),1,zeros(1,27)];% 该数组前1-5为0,6位为1,后27位为0
y=[zeros(1,8),ones(1,28)];% 该数组前1-5位为0,后28位为1
subplot(2,1,1);
stem(n,x,&#39;fill&#39;);grid on;
subplot(2,1,2)
stem(n,y,&#39;fill&#39;);grid on;
运行结果:
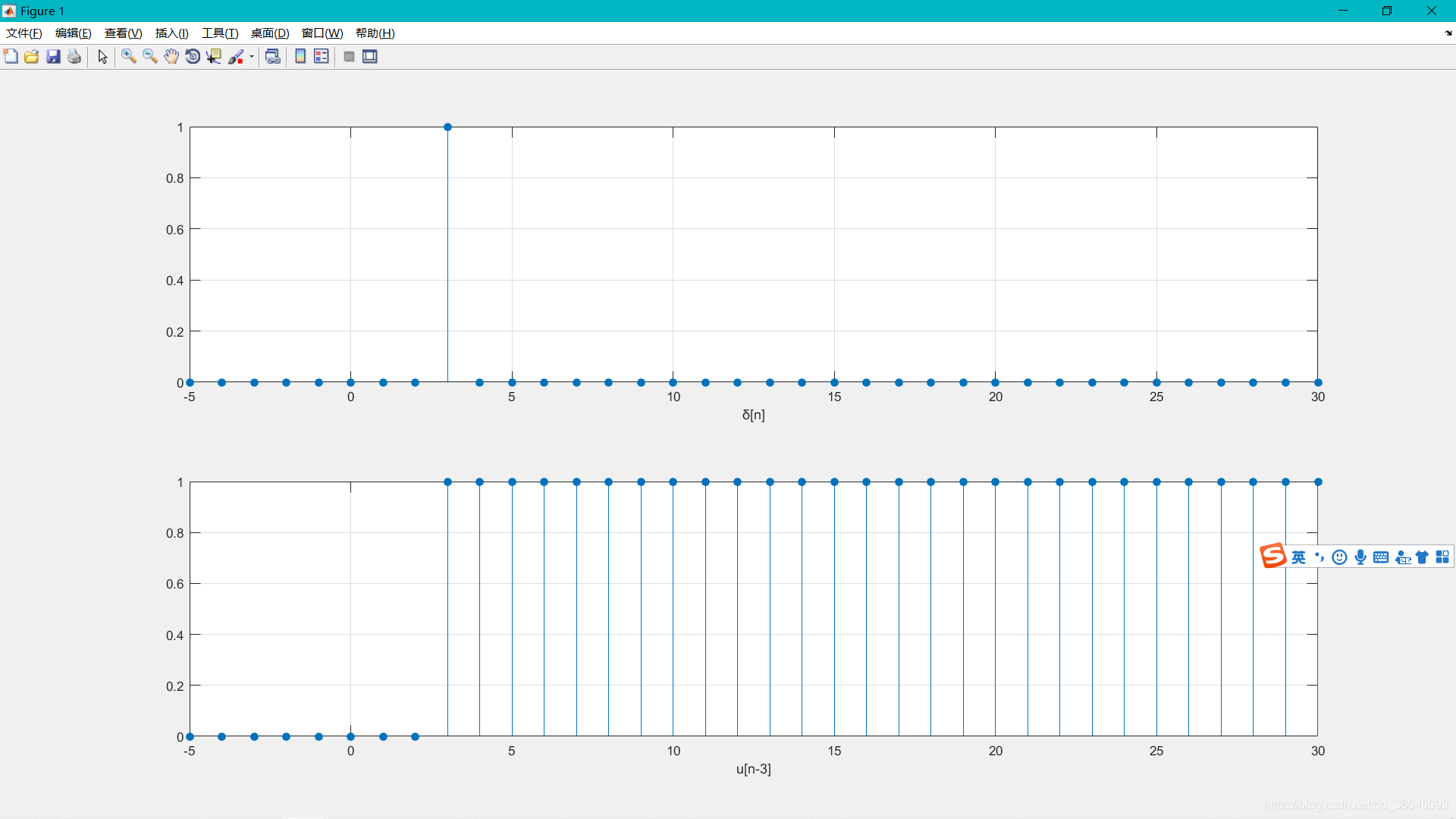
• 离散卷积
• matlab 中卷积运算的指令是c=conv(a,b),其中a和b是有限长的序列
例七 计算下面两个序列的卷积
a=[-2 0 1 –1 3]; b=[1 2 0 -1];
两个序列的都从0开始的
a=[-2 0 1 -1 3];% L(a)=5
b=[1 2 0 -1];% L(b)=4
c=conv(a,b);% L(c)=8
M=length(c)-1;% a卷积b的长度为L(a)+L(b)-1, L(M)=7
n=0:1:M;% n=0:1:7 L(N)=8
stem(n,c,&#39;fill&#39;);grid on;
xlabel(&#39;Time index n&#39;);% 给横坐标加注释
运行结果:
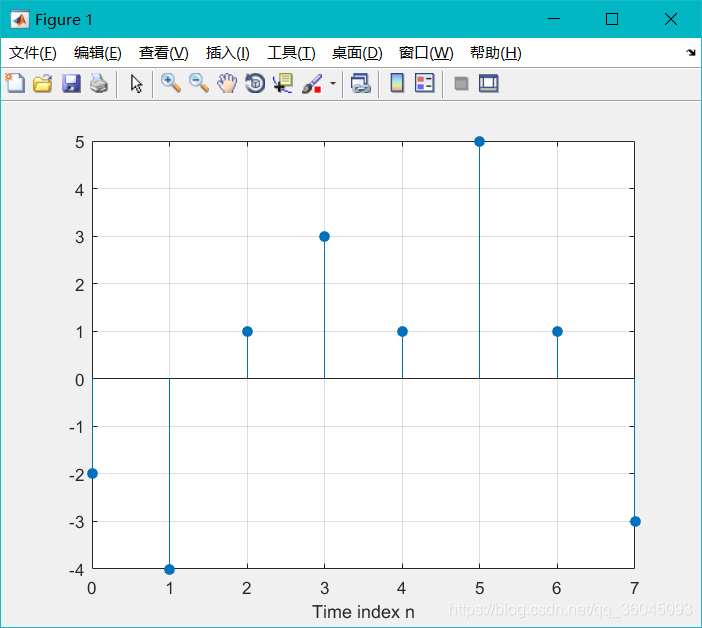
• LTI系统
• 因果LTI系统的零状态响应,在matlab中可以用函数y=filter(num,den,x) 实现
其中:
num------系统传递函数分子系数组成的行向量
den-------- 系统传递函数分母系数组成的行向量
x-------输入的离散序列
y-------输出的离散序列,y的长度与x的长度一样
• 因果LTI系统的幅频响应和相频响应曲线,在matlab中可以用函数freqz(num,den,n,Fs)
该函数可以同时作出幅频和相频响应图
其中:
num-----系统传递函数分子系数组成的行向量
den------系统传递函数分母系数组成的行向量
n---------是频率响应的点数,最好为2的幂缺省值512
Fs--------采样频率
例八 已知一个系统的传递函数为
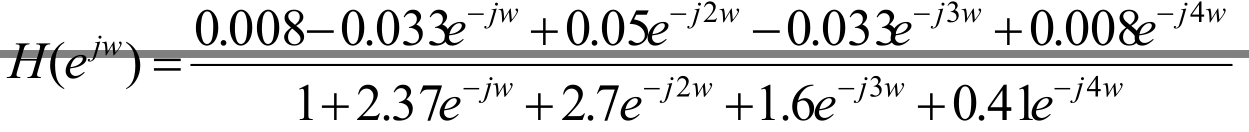
求系统单位冲激响应h[n],以及h[n]的幅频相频响应图
运行结果:
N=64;
x=[1 zeros(1,N-1)]; %产生单位冲激函数δ[n]
num=[0.008 -0.033 0.05 -0.033 0.008];% 分子系数
den=[1 2.37 2.7 1.6 0.41];% 分母系数
y=filter(num,den,x); %计算零状态响应以画出单位冲激响应h[n]
figure(1);% 画图1
n=1:N;
stem(n,y,&#39;fill&#39;);grid on; title(&#39;单位冲激响应&#39;);
figure(2)% 画图2
Fs=1024;
freqz(num,den,N,Fs);grid on; %做出幅频和相频响应曲线
title(&#39;幅频相频响应&#39;)
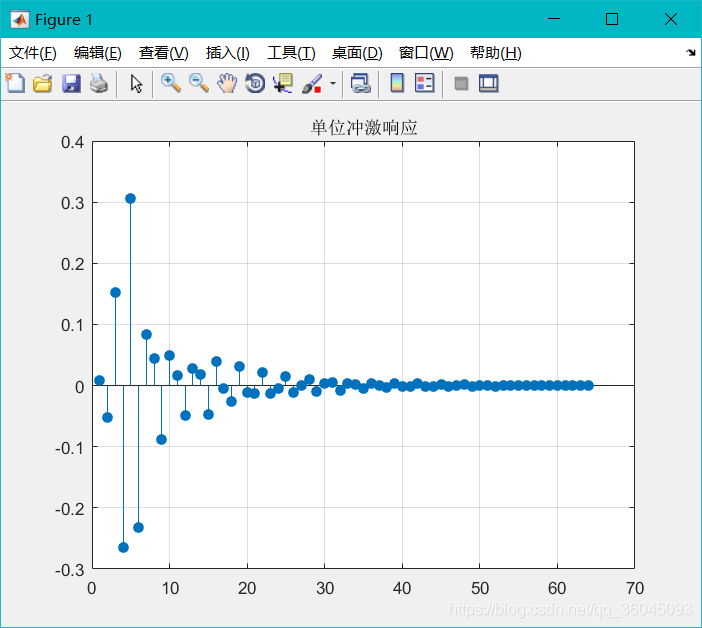

补充:
单边指数序列
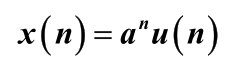
n=0:10;
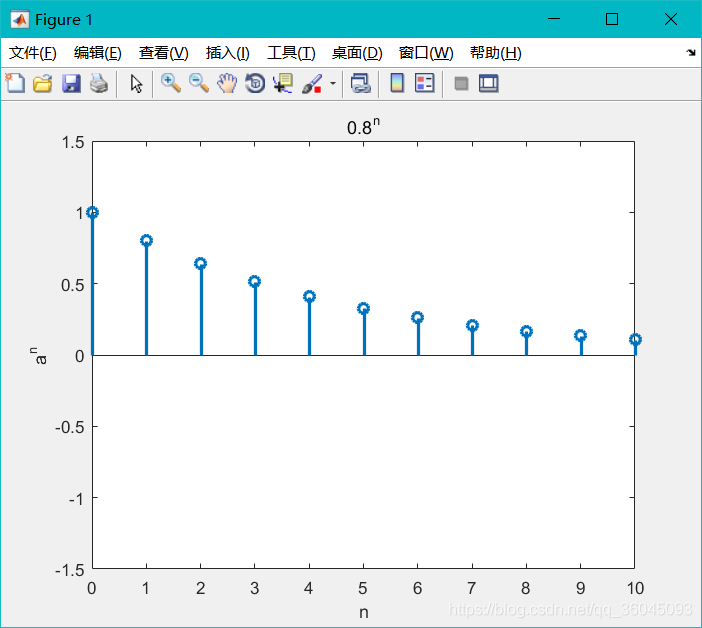
x1=power(0.8,n);
stem(n,x1,&#39;linewidth&#39;,2);
xlabel(&#39;n&#39;);
ylabel(&#39;a^n&#39;);
axis([n(1) n(end) -1.5 1.5]);
title(&#39;0.8^n&#39;);
运行结果:
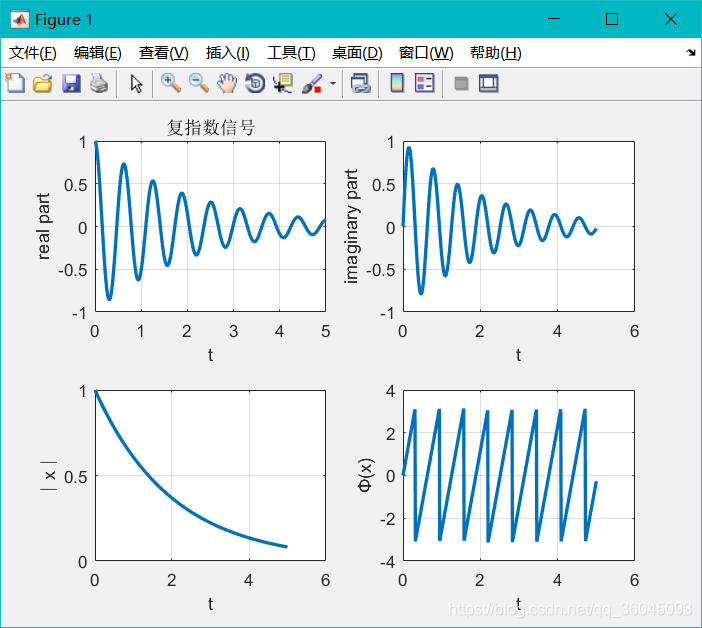
连续复指数信号
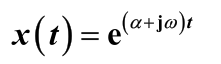
ts=0;
te=5;
dt=0.01;
t=[ts:dt:te];% t:0-5
alpha=-0.5;w=10;% 参数设置
x=exp((alpha+j*w)*t);
title(&#39;复指数信号&#39;);
subplot(2,2,1);plot(t,real(x),&#39;linewidth&#39;,2);% Re(x)
title(&#39;复指数信号&#39;);
xlim([t(1) t(end)]);
grid on;xlabel(&#39;t&#39;);ylabel(&#39;real part&#39;);subplot(2,2,2);plot(t,imag(x),&#39;linewidth&#39;,2);
grid on;xlabel(&#39;t&#39;);ylabel(&#39;imaginary part&#39;);subplot(2,2,3);plot(t,abs(x),&#39;linewidth&#39;,2);
grid on;xlabel(&#39;t&#39;);ylabel(&#39;∣x∣&#39;);subplot(2,2,4);plot(t,angle(x),&#39;linewidth&#39;,2);
grid on;xlabel(&#39;t&#39;);ylabel(&#39;Φ(x)&#39;);
运行结果:
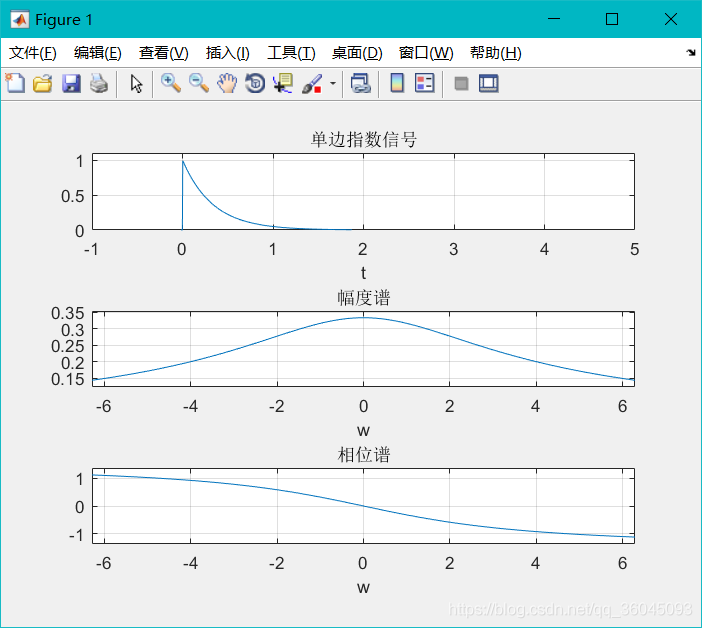
求连续非周期信号的幅频响应与相频响应曲线
exp(-3*t)*u(t)
% exp(-3*t)*u(t)的幅频、相频曲线
x=sym(&#39;exp(-3*t)*heaviside(t)&#39;);
subplot(311)
ezplot(x),grid on
axis([-1 5 0 1.1])
title(&#39;单边指数信号&#39;)
X=simplify(fourier(x));
subplot(312)
ezplot(abs(X)),grid on
title(&#39;幅度谱&#39;);
phase = angle(X);
subplot(313)
ezplot(phase),grid on
title(&#39;相位谱&#39;)
运行结果:
在实际应用中,经过抽样所获得的信号是离散的数值量x(k),无法表示为符号表达式,对于此类信号不能使用fourier函数进行处理,但是可以用MATLAB数值计算法进行求解。