数学系列-概率论-泊松分布和(负)指数分布简单概率分布图的意义

本文主要介绍关于概率论的知识点，对【数学系列 - 概率论 - 泊松分布和(负)指数分布】和【简单概率分布图的意义】有兴趣的朋友可以看下由【奶油松果】投稿的技术文章，希望该技术和经验能帮到你解决你所遇的【】相关技术问题。

简单概率分布图的意义

概率论-泊松分布和负指数分布 1. 泊松分布（1）引语（2）含义与公式（3）泊松分布图像：(4)期望与方差： 2.(负)指数分布(1) 例子(2) 含义与公式(3)图像

参考链接1
参考链接2

1. 泊松分布 （1）引语

日常生活中，有很多事情是有固定频率的。我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。

（2）含义与公式

泊松分布就是描述某段时间内，事件具体的发生概率。

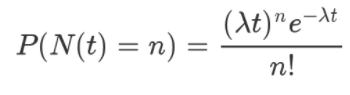
公式解释：
等号的左边，P 表示概率，N表示某种函数关系，t 表示时间，n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) 。
等号的右边，λ 表示事件的频率。

（3）泊松分布图像：

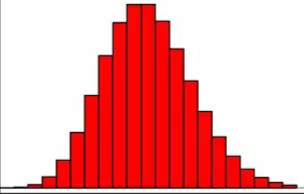
在频率附近，事件的发生概率最高，然后向两边对称下降，即变得越大和越小都不太可能。每小时出生3个婴儿，这是最可能的结果，出生得越多或越少，就越不可能。

(4)期望与方差：

泊松分布的期望和方差

由泊松分布知E[N(t) ? N(t0)] = D[N(t) ? N(t0)] = λ(t ? t0)
特别的，令t_0=0.由于假设N(0)=0,故可推知泊松过程的均值函数和方差函数分别为E[N(t)] = λt,D[N(t)] = λt,
泊松过程的强度lambda （常数）等于单位长时间间隔内出现的质点数目的期望值。即对泊松分布有：E(X) = D(X) = λ

2.(负)指数分布 (1) 例子

这些例子都属于指数分布

婴儿出生的时间间隔来电的时间间隔奶粉销售的时间间隔网站访问的时间间隔 (2) 含义与公式

指数分布是事件的时间间隔的概率。
如果下一个婴儿间隔时间 t ，就等同于 t 之内没有任何婴儿出生。

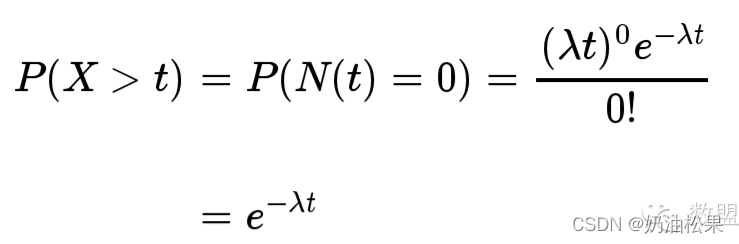
(3)图像

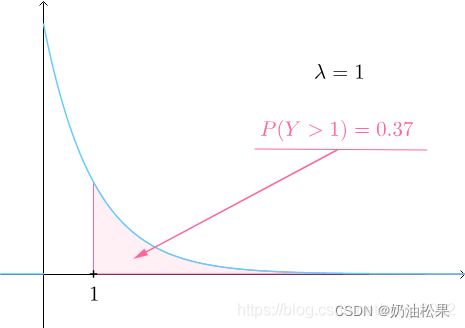
随着间隔时间变长，事件的发生概率急剧下降，呈指数式衰减。想一想，如果每小时平均出生3个婴儿，上面已经算过了，下一个婴儿间隔2小时才出生的概率是0.25%，那么间隔3小时、间隔4小时的概率，是不是更接近于0？

本文《数学系列 - 概率论 - 泊松分布和(负)指数分布》版权归奶油松果所有，引用数学系列 - 概率论 - 泊松分布和(负)指数分布需遵循CC 4.0 BY-SA版权协议。