数据挖掘知识点串烧：逻辑回归

本文为数据茶水间群友原创&＃xff0c;经授权在本公众号发表。

关于作者&＃xff1a;DD-Kylin&＃xff0c;一名喜欢编程与机器学习的统计学学生&＃xff0c;勤学好问&＃xff0c;乐于钻研&＃xff0c;期待跟大家多多探讨机器学习的相关内容~

0x00 前言

我们知道&＃xff0c;回归模型可以解决因变量为连续变量的问题&＃xff0c;但是&＃xff0c;如果因变量为分类变量的话&＃xff0c;用回归的方法就行不通了。这个时候我们就得选择用其他的分类方法了&＃xff0c;如决策树、随机森林、SVM等。而本篇文章要说的逻辑回归也是一种很好的分类方法。我们需要明确的一点是&＃xff0c;逻辑回归虽然是“回归”&＃xff0c;但是它本质上是一种二分类算法&＃xff0c;用来处理二分类问题的。

0x01 走近逻辑回归

问题1&＃xff1a;你能说说什么是逻辑回归吗&＃xff1f;

回答&＃xff1a;逻辑回归是一种二分类算法&＃xff0c;一般用来解决二分类问题&＃xff0c;但是它也可以用来解决多分类问题&＃xff0c;当使用它来解决多分类问题的时候&＃xff0c;由于逻辑回归的特点&＃xff0c;我们一般将多分类问题转化为二分类问题。这里多分类问题的转化有三种拆分策略&＃xff0c;分别是一对一、一对其余和多对多。通过多分类拆分策略&＃xff0c;我们可以使用逻辑回归来进行多分类问题的预测。但是这种方法我们一般不用&＃xff0c;因为多分类问题我们可以使用随机森林、朴素贝叶斯、神经网络这些更好的算法进行预测。

问题2&＃xff1a;逻辑回归是二分类算法&＃xff0c;那它究竟是如何进行分类的&＃xff1f;

回答&＃xff1a;逻辑回归是通过判断数据属于某一类的概率值大小来决定要将该数据判为哪一类。这里需要引入sigmoid函数(Y &＃61; 1/(1&＃43;e^-z) , 其中z &＃61; w^Tx&＃43;b

0x02 再会逻辑回归

问题1&＃xff1a;逻辑回归进行分类时的阈值是一定的吗&＃xff1f;可不可以人为地进行调整呢&＃xff1f;

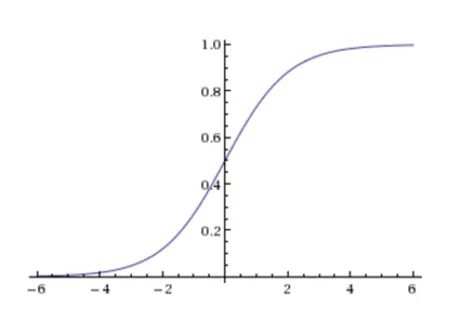
回答&＃xff1a;不一定。可以通过人为地进行修改的。逻辑回归输出的是概率&＃xff0c;即将Sigmoid函数输出的y视为正例的可能性&＃xff0c;我们可以自定义分类阈值来改变分类的结果。

问题2&＃xff1a;逻辑回归中的极大似然法是用来做什么的&＃xff1f;

回答&＃xff1a;因为sigmoid函数中&＃xff0c;z &＃61; w^Tx&＃43;b,其中 w和b都是未知的&＃xff0c;使用极大似然估计法是为了求出w和b使得每个样本属于其真实标记的概率值越大越好。 但是最大化似然函数的求解有点困难&＃xff0c;所以将其转为求解最小值&＃xff0c;即在求得的目标似然函数前面加上一个负号转为求解最小值。由于改变符号后的目标函数是高阶可导连续凸函数&＃xff0c;于是可以使用梯度下降法、牛顿法等来求解它的最小值&＃xff0c;通过函数的转化就可以较为轻松地求出w和b&＃xff0c;进而也就能知道sigmoid函数的输出了。

注&＃xff1a;逻辑回归是一种判别模型

问题3:逻辑回归有哪些应用&＃xff1f;

回答&＃xff1a;逻辑回归的应用其实跟它的算法特点有很大的关系。由于逻辑回归是一种性能很好的二分类算法。所以逻辑回归几乎可以应用于任何需要二分类的问题。如癌症检测、垃圾邮件分类、广告点击预测、医疗效果分析等。

0x03 优点VS缺点

问题:逻辑回归的优点是什么&＃xff1f;缺点又是什么&＃xff1f;

回答&＃xff1a;

逻辑回归的优点分别是&＃xff1a;

• 1、形式简单&＃xff0c;模型的可解释性非常好。从特征的权重可以看到不同的特征对结果的影响程度。如果特征的权重较大&＃xff0c;则说明这个特征对数据结果的影响程度较大。
• 2、它不是仅仅预测出类别&＃xff0c;还能知道近似概率预测&＃xff0c;这对许多需利用概率辅助决策的任务很有用。
• 3、逻辑回归求解的目标函数是任意可导的凸函数&＃xff0c;有很好的数学性质&＃xff0c;现有的许多优化算法都能直接用于求解最优值

逻辑回归的缺点分别是&＃xff1a;

• 1、很难处理数据不平衡的问题。举个栗子&＃xff0c;如果某个平台用户不下单与用户下单的数量比为10000&＃xff1a;50&＃xff0c;那么这个数据是一个类别很不平衡的数据&＃xff0c;机器可以把所有的样本都预测为用户不下单&＃xff0c;这样也可以使损失函数变得很小。但是作为一个分类器&＃xff0c;它对正负样本的分类就显得很不友好了。
• 2、逻辑回归本身无法筛选特征&＃xff0c;如果特征高度相关&＃xff0c;会拉低训练的速度。而特征数量过多的时候&＃xff0c;则会造成过拟合现象。
• 3、逻辑回归处理非线性的问题较为麻烦。逻辑回归在不引入其它方法的情况下&＃xff0c;只能处理线性可分的问题或者说是二分类的问题。

0x04 总结

关于逻辑回归&＃xff0c;我一直觉得它是一个很简单但是很强大的算法&＃xff0c;直到在写这篇文章的时候&＃xff0c;才发现原来它有那么多知识点需要理解。本文也只是起到一个抛砖引玉的作用&＃xff0c;如果大家想了解更多的话&＃xff0c;建议各位可以去看一下书&＃xff0c;练一下真实的案例&＃xff0c;肯定可以收获更多的理解&＃xff01;下面留几个讨论题&＃xff1a;

• 1、逻辑回归输出的概率值是真实的概率吗&＃xff1f;
• 2、逻辑回归中是如何区别正例跟反例的呢&＃xff1f;
• 3、如何衡量逻辑回归的模型效果&＃xff1f;
• 4、手推逻辑回归~

更多数据挖掘内容&＃xff1a;

数据挖掘面试题之&＃xff1a;梯度提升树

数据挖掘面试题之&＃xff1a;朴素贝叶斯

数据挖掘面试题之&＃xff1a;生成模型 VS 判别模型

数据挖掘知识点串烧&＃xff1a;SVM

特征工程系列&＃xff1a;数据清洗

特征工程系列&＃xff1a;特征筛选的原理与实现&＃xff08;上&＃xff09;

特征工程系列&＃xff1a;特征筛选的原理与实现&＃xff08;下&＃xff09;

特征工程系列&＃xff1a;特征预处理&＃xff08;上&＃xff09;

特征工程系列&＃xff1a;特征预处理&＃xff08;下&＃xff09;