目录

一、问题提出

数据依赖与冗余

二、函数依赖

2.1定义

2.2函数依赖类型

2.2.1函数依赖

2.2.2平凡函数依赖与非平凡函数依赖

2.2.3完全函数依赖与部分函数依赖

2.2.4传递函数依赖

2.3函数依赖的推导

2.3.1 Armstrong公理

2.3.2属性集的闭包

2.3.3函数依赖集的极小覆盖

三、范式

3.1码

3.2范式种类

3.2.1 1NF

3.2.2 2NF

3.2.3 3NF与 BCNF

四、关系模式分解

4.1无损连接分解

4.2保持函数依赖的分解

五、关系模式分解成高级范式

5.1具有无损连接性的 BCNF分解

5.2具有无损连接性和保持函数依赖的 3NF分解

• 关系名R是符号化的元组语义
• U为一组属性
• D为属性组U中的属性所来自的域
• DOM为属性到域的映射
• F为属性组U上的一组数据依赖&＃xff08;关系内部属性与属性之间的一种约束关系&＃xff0c;主要分函数依赖和多值依赖&＃xff09;

由于D、DOM与模式设计关系不大&＃xff0c;本博客中把关系模式看作一个三元组&＃xff1a;R

一、问题提出

数据库设计的不好可能导致多个问题&＃xff1a;冗余&＃xff0c;修改异常&＃xff0c;插入异常&＃xff0c;删除异常

数据依赖与冗余

数据依赖是关于诸属性值之间内在相关性的陈述&＃xff0c;它规定了关系模式的合法关系实例所必须满足的条件&＃xff0c;可分为函数依赖和多值依赖

依赖和冗余是密不可分的&＃xff1a;承认某种数据依赖&＃xff0c;就能发现关系中的某些冗余&＃xff1b;而不承认数据之间的依赖关系&＃xff0c;也没理由认为某些信息是多余的

冗余的产生原因和处理总是联系在一起

二、函数依赖

2.1定义

字母表开头的大写字母 A,B,…,H表示单个属性

字母表尾部的大写字母 U,V,…,Z一般表示属性集&＃xff0c;也可能是由单个属性构成的集合。U常用于表示关系的全部属性组成的集合

串接表示并。A1A2…An表示集合 {A1,A2,…,An}&＃xff0c;XY是 X 

• 某一关系模式R为第n范式&＃xff0c;可简记为R∈nNF

一个低一级范式的关系模式&＃xff0c;通过模式分解可以转换为若干个高一级范式的关系模式的集合&＃xff0c;这种过程就叫规范化

3.2.1 1NF

条件&＃xff1a;每个分量必须是不可分开的数据项

解释&＃xff1a;在一列中不能插入两个及以上不同属性的值

3.2.2 2NF

定义&＃xff1a;对于任意的非平凡函数依赖 X->A 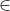 F&＃43;&＃xff0c;必须满足下列两个条件之一&＃xff1a;A是主属性&＃xff0c;或 X不是 R的任何码的真子集

解释&＃xff1a;第二范式&＃xff08;2NF&＃xff09;要求数据库表中的每个实例或记录必须可以被唯一地区分。选取一个能区分每个实体的属性或属性组&＃xff0c;作为实体的唯一标识&＃xff0c;即要有主码

举例&＃xff1a;如果在成绩表SG中添加一列姓名变成下面这样&＃xff0c;SG表的主码是学号加CID(课程号)&＃xff0c;但是&＃xff08;学号&＃xff09;->姓名&＃xff0c;所以姓名部分函数依赖于&＃xff08;学号&＃xff0c;CID(课程号)&＃xff09;&＃xff0c;不符合2NF

成绩表SG

成绩表SG 2.0

3.2.3 3NF与 BCNF

1、3NF

定义&＃xff1a;对于任意的非平凡函数依赖 X->A 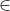 F&＃43;&＃xff0c;必须满足下列两个条件之一&＃xff1a;A是主属性&＃xff0c;或 X是 R的码&＃xff08;在2NF基础上消除传递依赖&＃xff09;

解释&＃xff1a;第三范式&＃xff08;3NF&＃xff09;要求一个关系中不包含已在其它关系已包含的非主属性信息

举例&＃xff1a;如果在课程表SC中添加一列老师姓名&＃xff0c;变成如下&＃xff0c;存在CID(课程号)->TID(授课老师ID)&＃xff0c;TID(授课老师ID)->教师姓名&＃xff0c;TID(授课老师ID) !->CID(课程号)&＃xff0c;所以教师姓名传递函数依赖于CID(课程号)&＃xff0c;不满足3NF&＃xff0c;但是满足2NF&＃xff0c;主码是CID

课程表SC

课程表SC 2.0

2、BCNF

对于任意的非平凡函数依赖 X->A 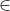 F&＃43;&＃xff0c;X是 R的码

范式总结

• 1NF&＃xff1a;关系模式的任何一个属性都是原子属性
• 2NF&＃xff1a;任一个非主属性都不能依赖于码的一部分
• 3NF&＃xff1a;任一个非主属性都不能传递依赖与码
• BCNF&＃xff1a;非主属性和主属性都不能依赖于码的一部分或传递依赖于码

四、关系模式分解

4.1无损连接分解

检测无损分解的连接性

输入&＃xff1a;关系模式 R(A1,A2,...,An)&＃xff0c;R的函数依赖集 F和分解 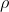 &＃61;{R1,R2,...Rk}

输出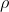&＃xff1a; 是否是关于 F的无损连接分解的判定

方法

1. 建立一张 n列 k行的表&＃xff0c;每一列对应一个属性&＃xff0c;每一行对应一个关系模式。若属性Aj 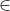 Ri&＃xff0c;则表的第 i 行第 j 列上为 aj&＃xff0c;否则为 bij
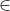2. 重复如下过程&＃xff0c;直到表不再变化&＃xff1a;在每一轮&＃xff0c;考察每个 X->Y  F。如果表中存在两行或多行在 X的属性上对应相同&＃xff0c;则按如下方法使得这些行在 Y上的符号相同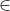&＃xff1a;对于每个 Aj  Y&＃xff0c;如果这些行存在 aj&＃xff0c;则将这些行的第 j 列都改为 aj&＃xff0c;否则将它们都改为 bij&＃xff0c;其中 i 是这些行的最小行号
3. 如果存在一行是a1...an&＃x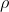ff0c;则  是无损连接分解&＃xff0c;否则不是

例&＃xff1a;关系模式 R(A,B,C,D,E)的分解是 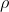 &＃61;{R1(A,B,C), R2(C.D), R3(D,E)}&＃xff0c;其中 R的函数依赖集 F&＃61;{AB->C,C->D,D->E}

解&＃xff1a;

构造初始表

A	B	C	D	E
a1	a2	a3	b14	b15
b21	b22	a3	a4	a5
b31	b32	b33	a4	a5

得出最终表

A	B	C	D	E
a1	a2	a3	a4	a5
b21	b22	a3	a4	a5
b31	b32	b33	a4	a5

第一行是a1a2a3a4a5&＃xf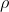f0c;所以  是无损连接分解

如果 R被分解成两个关系模式 R1和 R2&＃xff0c;可用如下简单方法进行判定

设 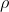 &＃61;{R1,R2}是关系模式 R的一个分解&＃xff0c;F是 R上的函数依赖集。 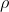关于 F是无损连接分解当且仅当&＃xff1a;

(R1 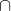 R2) -> (R2 - R1) 或 (R1  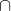R2) -> (R2 - R1)

4.2保持函数依赖的分解

输入&＃xff1a;关系模式 R的函数依赖集 F和分解 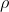 &＃61;{R1,R2,...,Rk}

输出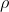&＃xff1a; 是否保持函数依赖的判定

方法

for (每个 X->Y包含于 F) do
beginif (不存在 i使得 XY包含于 Ri) then
--检验 X->Y是否被分解 p所保持beginZ&＃61;X;repeatfor i&＃61;1 to k doZ&＃61;Z 并 ((Z 交 Ri)&＃43; 交 Ri);until (Z不发生变化);if (Y不是 Z的子集) then -- X->Y不被分解 p所保持return p不是保持函数依赖的分解;end;
end;

无损连接是对关系模式分解的基本要求。不具有无损链接性的分解是有害的&＃xff0c;因为分解前后的关系模式可能不能反应相同的现实世界

保持函数依赖的分解是对关系模式分解的进一步要求。实践中应当在确保无损连接性的前提下尽可能地追求保持函数依赖。如果两者不可兼得&＃xff0c;优先考虑无损连接分解

五、关系模式分解成高级范式

任意关系模式都可以无损连接地分解成 BCNF

如果要求分解保持函数依赖&＃xff0c;或者保持函数依赖并且具有无损连接性&＃xff0c;则只能保证分解到 3NF

5.1具有无损连接性的 BCNF分解

只包含两个属性的关系模式一定是 BCNF

输入&＃xff1a;关系模式 R及 R的函数依赖集 F

输出&＃xff1a;R的 BCNF分解&＃xff0c;它关于 F具有无损连接性

方法

result&＃61;{R}
while (存在 Ri属于 result&＃xff0c;但 Ri不是 BCNF)
begin找出 Ri中满足如下条件的非平凡函数依赖&＃xff1a;X->Y属于F&＃43;&＃xff0c;且 X不是 Ri的超码;result&＃61;{Ri1(XY),Ri2(Ri-Y)};   --之后分别对新产生的模式进行该操作
end
return result;

例、关系模式R&＃xff0c;其中&＃xff1a;U&＃61;{A,B,C,D,E}&＃xff0c;F&＃61;{A→C,C→D,B→C,DE→C,CE→A}&＃xff0c;将其分解成BCNF并保持无损连接

解&＃xff1a;

L: ACBDE   R: CDA N:      LR: ACD

①令ρ&＃61;{R(U,F)}

②ρ中不是所有的模式都是BCNF&＃xff0c;转入下一步

③分解R&＃xff1a;R上的候选关键字为BE&＃xff08;因为所有函数依赖的右边没有BE&＃xff09;

   考虑A→C函数依赖不满足BCNF条件&＃xff08;因A不包含候选键BE&＃xff09;&＃xff0c;将其分解成R1(AC)、R2(ABDE)

   计算R1和R2的最小函数依赖集分别为&＃xff1a;F1&＃61;{A→C}&＃xff0c;F2&＃61;{B→D,DE→D,BE→A}

   其中B→D是由于R2中没有属性C且B→C,C→D&＃xff1b;DE→D是由于R2中没有属性C且DE→C,C→D&＃xff1b;BE→A是由于R2中没有属性C且B→C,CE→A。又由于DE→D是蕴含关系&＃xff0c;可以去掉&＃xff0c;故F2&＃61;{B→D, BE→A}

5.2具有无损连接性和保持函数依赖的 3NF分解

对于给定的关系模式 R&＃xff0c;先计算 F的极小覆盖&＃xff08;转顶部链接内容&＃xff1a;2.3.3函数依赖集的极小覆盖&＃xff09;

对于极小覆盖中的每个函数依赖&＃xff0c;只要依赖的左侧相同&＃xff0c;则合并这些函数依赖的所有属性构成一个单独的模式

如果关系模式 R中存在没有出现在函数依赖集中的元素&＃xff0c;这些元素合并构成一个单独的模式

如果上面两步得出的结果中不包含候选码&＃xff0c;则候选码单独构成一个模式&＃xff08;尽管候选码被拆散到多个模式中也不算&＃xff09;

例、关系模式R&＃xff0c;其中U&＃61;{C,T,H,R,S,G}&＃xff0c;F&＃61;{CS→G,C→T,TH→R,HR→C,HS→R}&＃xff0c;将其分解成3NF并保持函数依赖

解&＃xff1a;

(一)计算F的最小函数依赖集

①利用分解规则&＃xff0c;将所有的函数依赖变成右边都是单个属性的函数依赖。由于F的所有函数依赖的右边都是单个属性&＃xff0c;故不用分解

②去掉F中多余的函数依赖 F&＃61;{CS→G,C→T,TH→R,HR→C,HS→R}

   去掉F中各函数依赖左边多余的属性&＃xff08;只检查左部不是单个属性的函数依赖&＃xff09;&＃xff0c;没有发现左边有多余属性的函数依赖

   故最小函数依赖集为&＃xff1a;F&＃61;{CS→G,C→T,TH→R,HR→C,HS→R}

(二)由于R中的所有属性均在F中都出现&＃xff0c;所以转下一步

(三)对F按具有相同左部的原则分为&＃xff1a;

F&＃61;{CS→G,C→T,TH→R,HR→C,HS→R}

R1&＃61;CSG&＃xff0c;R2&＃61;CT&＃xff0c;R3&＃61;THR&＃xff0c;R4&＃61;HRC&＃xff0c;R5&＃61;HSR

所以 ρ&＃61;{ R1(CSG), R2(CT), R3(THR), R4(HRC), R5(HSR) }