作者:ht遨游遐想 | 来源:互联网 | 2024-09-28 15:08
下面来讲一下图的深度优先搜索的方法。
遍历原则:
从图中某一个指定的顶点v出发,先访问v,然后从该顶点未被访问过的邻接顶点w出发进行深度优先搜索,直到图中与v想通的所有顶点都被访问,此时相当于完成图中一个包含顶点v的连通分量的遍历。如果图中存在尚未遍历过的顶点,则从另一个未被访问的顶点出发重复上述过程,直到图中所有顶点均被遍历到。
显然,深度优先搜索算法是一种递归算法。
分析:
假设有一幅图,如下图所示。
![]()

该图的邻接表为:
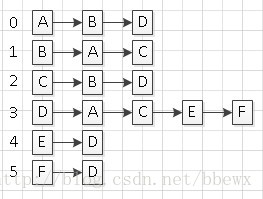
如果对该图进行深度优先搜索,步骤如下:
STEP1:从顶点A出发进行深度优先搜索。首先访问顶点A,并将A标注为已访问状态(图中标注为黄色),然后去找顶点A的第一个邻接点,如果第一个邻接点已被访问,则搜索顶点A的下一个邻接点。显然,顶点A的第一个邻接点为顶点B,且B未被访问。

STEP2:访问顶点B,并将B标注为已访问状态(图中标注为绿色),然后寻找顶点B的第一个邻接点,该邻接点为A,但是由于顶点A已经被访问过,因此继续寻找顶点B的下一个邻接点C,发现顶点C未被访问过。
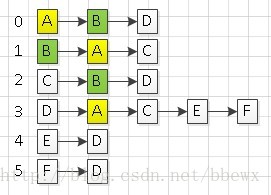
STEP3:访问顶点C,并将C标注为已访问状态(图中标注为橙色),寻找C的第一个邻接点B,因为B已经被访问,因此寻找下一个邻接点D,D未被访问过。

STEP4:访问顶点D,并将D标注为已访问状态(图中标注为蓝色),寻找D的第一个邻接点A,A已经被访问过,不断寻找D的下一个邻接点,知道找到第一个未被访问的顶点E。
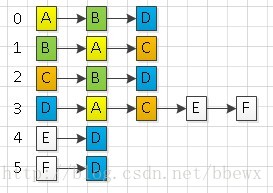
STEP5:访问顶点E,并将E标注为已访问状态(图中标注为红色),访问E的第一个邻接点D,发现D已经被访问过,然后去找E的下一个邻接点,发现没有邻接点,则返回上一层,也就是STEP4。

STEP6:寻找顶点D的下一个未被访问的邻接点F,访问顶点F,并将F标注为已访问状态(图中标注为紫色)。寻找F的第一个邻接点D,发现D已经被访问过,寻找F的下一个邻接点,发现没有邻接点,则返回上一层,也就是STEP4。
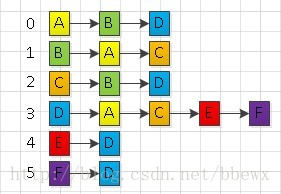
STEP7:寻找顶点D的未被访问的邻接点,发现不存在这样的邻接点,则返回STEP3层;寻找顶点C的未被访问的邻接点,发现不存在这样的邻接点,则返回STEP2层;寻找顶点B的未被访问的邻接点,发现不存在这样的邻接点,则返回STEP1层;寻找顶点A的未被访问的邻接点,发现不存在这样的邻接点,则退出程序。此时,图中各个顶点的访问便结束了。
代码:
1.定义图的顶点结构体VLink以及边的结构体ELink,并设置一个数组visited,该数组用来标记顶点是否被访问。例如:若visited[0]=0,说明下标为0的顶点未被访问,若visited[3]=1,说明下标为3的顶点被访问了。
#define MAXNUM 100
int visited[MAXNUM];
typedef struct edge {
int adjvex;
edge* next;
}ELink;
typedef struct ver {
char vertex;
ELink* link;
}VLink;
2.定义深度优先搜索的主算法。
void TRAVER_DFS(VLink G[], int vSize, int visited[]) {
//初始化访问数组
for(int i=0; i
3.定义深度优先搜索DFS算法。
void DFS( VLink G[], int v ) {
int w;
cout <
4.定义寻找顶点v的第一个邻接点的函数FirstADJ
int FirstADJ( VLink G[], int v ) {
ELink *p = G[v].link;
if(p) {
return p->adjvex;
}
else {
return -1;
}
}
5.定义寻找顶点v的下一个未被访问的邻接点的函数NextADJ
int NextADJ( VLink G[], int v ) {
ELink *p = G[v].link;
while(p) {
if(visited[p->adjvex] == 0) {
return p->adjvex;
}
p = p->next;
}
return -1;
}
6.定义打印图的邻接表的函数
void printADJLIST(VLink G[], int vSize) {
ELink *p;
for(int i=0; i" <adjvex;
p = p->next;
}
cout <
7.定义主函数
int _tmain(int argc, _TCHAR* argv[])
{
VLink vArray[6];
for(int i=0; i<6; i++) {
vArray[i].vertex = 'A' + i;
vArray[i].link = NULL;
}
ELink* edge1 = new ELink;
ELink* edge2 = new ELink;
ELink* edge3 = new ELink;
ELink* edge4 = new ELink;
ELink* edge5 = new ELink;
ELink* edge6 = new ELink;
ELink* edge7 = new ELink;
ELink* edge8 = new ELink;
ELink* edge9 = new ELink;
ELink* edge10 = new ELink;
ELink* edge11 = new ELink;
ELink* edge12 = new ELink;
edge1->adjvex = 1; edge1->next = edge2;
edge2->adjvex = 3; edge2->next = NULL;
edge3->adjvex = 0; edge3->next = edge4;
edge4->adjvex = 2; edge4->next = NULL;
edge5->adjvex = 1; edge5->next = edge6;
edge6->adjvex = 3; edge6->next = NULL;
edge7->adjvex = 0; edge7->next = edge8;
edge8->adjvex = 2; edge8->next = edge9;
edge9->adjvex = 4; edge9->next = edge10;
edge10->adjvex = 5; edge10->next = NULL;
edge11->adjvex = 3; edge11->next = NULL;
edge12->adjvex = 3; edge12->next = NULL;
vArray[0].link = edge1;
vArray[1].link = edge3;
vArray[2].link = edge5;
vArray[3].link = edge7;
vArray[4].link = edge11;
vArray[5].link = edge12;
printADJLIST(vArray, 6);
TRAVER_DFS(vArray, 6, visited);
delete edge1;
delete edge2;
delete edge3;
delete edge4;
delete edge5;
delete edge6;
delete edge7;
delete edge8;
delete edge9;
delete edge10;
delete edge11;
delete edge12;
return 0;
}
输出结果如下:
