《数据结构》学习笔记3——串匹配算法性能评估

/*.. 前言：感谢学堂在线的学习资源！！！感谢邓公！！本文代码均整理自课件 ..*/

通常，字符种类不多，而串长>>字符种类数量。

% grep             定义：模式P   文本T

Pattern matching: detection? location? counting? enumeration?（本文主要讨论出现位置）

数据结构，借助C++中头文件：

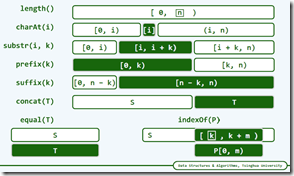
详情参考 http://www.cplusplus.com/reference/cstring/    http://www.cplusplus.com/reference/string/string/

算法性能评估：随机T，对成功、失败的匹配分别测试（成功，在T中，随机取出长度为m的子串作为P，分析平均复杂度；失败，采用随机P，统计平均复杂度）

蛮力算法：O(m*n)

1 int match_BruteForce(char * P, char * T) {
2 size_t n = strlen(T), i = 0;
3 size_t m = strlen(P), j = 0;
4 for (i = 0; i <= n - m; ++i) {
5 for (j = 0; j j)
6 if (T[i + j] != P[j]) break;
7 if (m <= j) break; // 找到匹配子串
8 }
9 return (i > n - m ) ? -1 : i; // 返回-1表示匹配失败。
10 }

int match_BruteForce(char * P, char * T)

KMP算法（Kunth  Morris  Pratt三位大家)：O(m+n)

相比蛮力算法优化：P快速右移，避免重复比对(利用成功匹配的经验，构造next表)。

【下图1体会KMP比对过程，优化前的next表】【图2 next表构造思路】【图3自绘优化后的next表构造程序流程图，啊哈哈哈】

当使用蛮力算法，单次匹配概率越小时（比如P中为较少出现的字符），此时最好情况接近O(n)，KMP相比蛮力算法优势不明显。而例如二进制串匹配，则KMP算法性能优势明显。 

1 int match_KMP(char * P, char * T) {
2 int * next = buildNext(P);
3 int n = (int)strlen(T), i = 0;
4 int m = (int)strlen(P), j = 0;
5 while (j n)
6 if (j <0 || T[i] == P[j]) { // 匹配
7 i++; j++;
8 }
9 else // 失败
10 j = next[j];
11 delete[] next;
12 // return i - j; // 返回
13 return (i - j > n - m) ? -1 : i; // 返回-1表示匹配失败。
14 }

int match_KMP(char * P, char * T)

BM_BC算法 [ Boyer + Moore, 1997] ：最好O(n/m)，最差O(n*m) （坏字符 Bad Character – 失败教训）

相比KMP算法，由于越靠后的位置，作用越大，因此对模式串P从后向前匹配。（利用匹配失败的经验）

构建bc表：记录全字符在匹配串中的位置，在匹配失败时【右】移动至匹配的位置，使得当前匹配成功。

优点：单次匹配概率越小时，性能优势越明显（大字母表，特别是Unicode）；P越长，移动效果越明显。

缺点：单次匹配概率越大的场合，性能越接近蛮力算法（小字母表，DNA）。

1 int * buildBC(char * P) {
2 int * bc = new int[256]; //bc表，与字母表等长
3 for (size_t j = 0; j <256; ++j) bc[j] = -1; // 此初始化可省略
4 for (size_t m = strlen(P), j = 0; j )
5 bc[P[j]] = j; //不断覆盖P[j]的出现位置
6 return bc;
7 }

int * buildBC(char * P)

BM_GS算法 ：兼顾BM_BC算法和KMP算法的思路（好后缀 Good Suffix – 成功经验）

【下图体会一下同时考虑匹配好后缀，和坏字符的策略】

性能比较：BM_GS算法最坏O(n/m)，最好O(m+n)

Karp-Rabin 算法：串即是数！（这是一种思想！）

算法：散列+ 相邻串的位运算O(1)

利用散列（模余函数）对串进行筛选，再进一步确认是否匹配；每一次筛选，即从上一个串的散列值到下一个串的散列值，计算只需要O(1)时间。