https://blog.csdn.net/yiwei151/article/details/87946592
效果图:
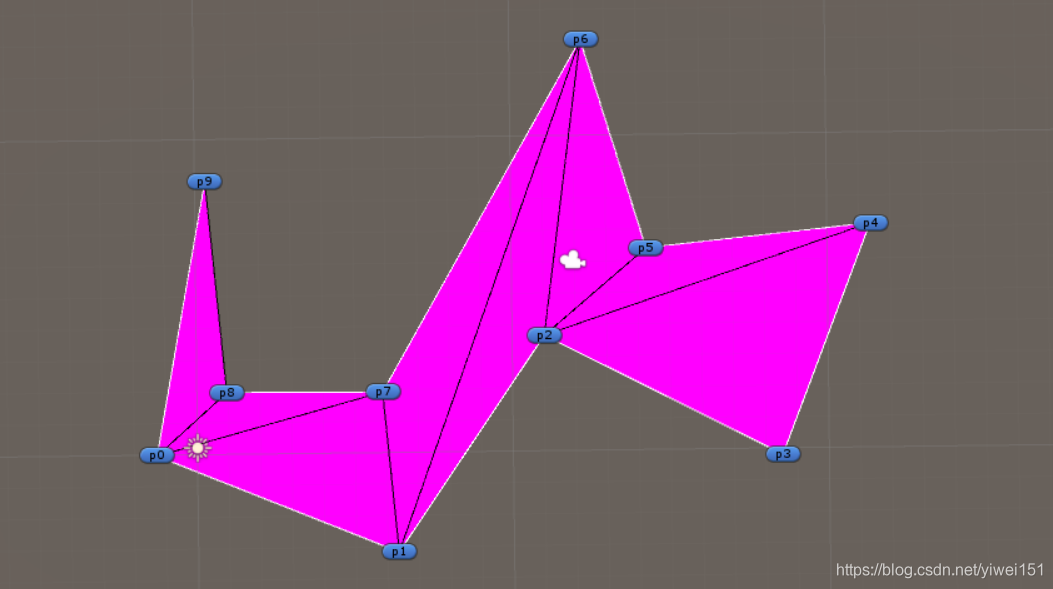
做法及原理可参考此链接:http://www.cnblogs.com/xignzou/p/3721494.html
代码:
using System;
using System.Collections.Generic;
using UnityEngine;
namespace PolygonTool
{
#region 耳切法对简单多边形进行三角形化
///
/// 判断凹点,凸点,耳朵的比较轴
///
public enum CompareAxle
{
X,
Y,
Z
}
///
/// 对多边形处理
///
public class Triangulation
{
///
/// 判断凹凸的时候的比对轴
///
private CompareAxle _compareAxle = CompareAxle.Y;
///
/// 多边形顶点
///
private List
///
/// 顶点序列
///
private List
///
/// 节点管理器
///
private NodeManager _nodeManager = new NodeManager();
///
/// 初始化
///
/// 多边形顶点
public Triangulation(List
{
this._polygOnVertexs= polygonVertexs;
_nodeManager.Init(polygonVertexs);
}
///
/// 设置比较轴
///
///
public void SetCompareAxle(CompareAxle compareAxle)
{
this._compareAxle = compareAxle;
}
///
/// 获取三角形的顶点序列
///
public int[] GetTriangles()
{
while (_nodeManager.LinkedListLength >= 3)
{
SplitResult sr = SplitPolygon();
//
if (sr == null)
{
Debug.Log("null");
return null;
}
}
return _vertexsSequence.ToArray();
}
///
/// 计算凹顶点,凸顶点,耳朵
///
private SplitResult SplitPolygon()
{
//凹点
List
//凸点
List
//耳朵
List
//起始节点
Node currentNode = _nodeManager.FirstNode;
#region 计算凹顶点,凸顶点
for (int i = 0; i <_nodeManager.LinkedListLength; i++)
{
Vector3 One= currentNode.vertex - currentNode.lastNode.vertex;
Vector3 two = currentNode.nextNode.vertex - currentNode.vertex;
Vector3 crossRes = Vector3.Cross(one, two);
if (_compareAxle == CompareAxle.Y)
{
if (crossRes.y > 0)
{
_concaveVertexs.Add(currentNode);
}
else
{
_raisedVertexs.Add(currentNode);
}
}
if (_compareAxle == CompareAxle.X)
{
if (crossRes.x > 0)
{
_concaveVertexs.Add(currentNode);
}
else
{
_raisedVertexs.Add(currentNode);
}
}
if (_compareAxle == CompareAxle.Z)
{
if (crossRes.z > 0)
{
_concaveVertexs.Add(currentNode);
}
else
{
_raisedVertexs.Add(currentNode);
}
}
_polygonEars.Add(currentNode);
currentNode = currentNode.nextNode;
}
for (int i = 0; i <_concaveVertexs.Count; i++)
{
_polygonEars.Remove(_concaveVertexs[i]);
}
#endregion
#region 计算耳朵
List
for (int i = 0; i <_polygonEars.Count; i++)
{
Node earNode = _polygonEars[i];
Node compareNode = earNode.nextNode.nextNode;
while (compareNode != earNode.lastNode)
{
bool isIn = IsIn(compareNode.vertex, earNode.lastNode.vertex, earNode.vertex,
earNode.nextNode.vertex);
if (isIn == true)
{
if (_polygonEars.Contains(_polygonEars[i]))
{
needRemoveIdList.Add(_polygonEars[i].id);
}
break;
}
compareNode = compareNode.nextNode;
}
}
for (int j = 0; j
for (int i = 0; i <_polygonEars.Count; i++)
{
if (_polygonEars[i].id == needRemoveIdList[j])
{
_polygonEars.RemoveAt(i);
}
}
}
#endregion
#region 打印初始化结果
Debug.Log("凸点");
for (int i = 0; i <_raisedVertexs.Count; i++)
{
Debug.Log(_raisedVertexs[i].id);
}
Debug.Log("凹点");
for (int i = 0; i <_concaveVertexs.Count; i++)
{
Debug.Log(_concaveVertexs[i].id);
}
Debug.Log("耳朵");
for (int i = 0; i <_polygonEars.Count; i++)
{
Debug.Log(_polygonEars[i].id);
}
Debug.Log("-----------------------------------------------");
#endregion
//耳朵为空说明不是简单多边形 多边形三角化失败
if (_polygonEars.Count == 0)
{
return null;
}
_vertexsSequence.Add(_polygonEars[0].lastNode.id);
_vertexsSequence.Add(_polygonEars[0].id);
_vertexsSequence.Add(_polygonEars[0].nextNode.id);
_nodeManager.RemoveNode(_polygonEars[0]);
return new SplitResult(_raisedVertexs, _concaveVertexs, _polygonEars);
}
///
/// 判断一点是否在三角形内
///
/// 一点
///
///
///
///
public bool IsIn(Vector3 p,Vector3 a,Vector3 b,Vector3 c)
{
Vector3 pa = p - a;
Vector3 pb = p - b;
Vector3 pc = p - c;
Vector3 t1 = Vector3.Cross(pa, pb);
Vector3 t2 = Vector3.Cross(pb, pc);
Vector3 t3 = Vector3.Cross(pc, pa);
bool isIn2 = t1.y >= 0 && t2.y >= 0 && t3.y >= 0 || t1.y <= 0 && t2.y <= 0 && t3.y <= 0;
return isIn2;
}
///
/// 管理多边形 构成一个双向链表
///
public class NodeManager
{
private List
public int LinkedListLength
{
get { return _nodeList.Count; }
}
public Node FirstNode
{
get { return _nodeList[0]; }
}
public void Init(List
{
for (int i = 0; i
Node node = new Node(i, vertexs[i]);
_nodeList.Add(node);
}
for (int i = 0; i {
if (i == 0)
{
_nodeList[i].lastNode = _nodeList[LinkedListLength - 1];
_nodeList[i].nextNode = _nodeList[1];
}
else if (i == LinkedListLength - 1)
{
_nodeList[i].lastNode = _nodeList[LinkedListLength - 2];
_nodeList[i].nextNode = _nodeList[0];
}
else
{
_nodeList[i].lastNode = _nodeList[i - 1];
_nodeList[i].nextNode = _nodeList[i + 1];
}
}
}
public void RemoveNode(Node node)
{
_nodeList.Remove(node);
node.lastNode.nextNode = node.nextNode;
node.nextNode.lastNode = node.lastNode;
}
}
public class Node
{
public int id;
public Vector3 vertex;
public Node lastNode;
public Node nextNode;
public Node(int id, Vector3 vertex)
{
this.id = id;
this.vertex = vertex;
}
public Node(int id, Vector3 vertex, Node lastNode, Node nextNode)
{
this.id = id;
this.vertex = vertex;
this.lastNode = lastNode;
this.nextNode = nextNode;
}
}
public class SplitResult
{
///
/// 凸顶点
///
public List
///
/// 凹顶点
///
public List
///
/// 耳朵
///
public List
public SplitResult(List
{
this.raisedVertexs = raisedVertexs;
this.cOncaveVertexs= concaveVertexs;
this.polygOnEars= polygonEars;
}
}
}
#endregion
}
github地址:https://github.com/yiwei151/PolygonTriangulation
使用耳切法将多边形三角化【转】

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有