作者:l沈佩玉iVf | 来源:互联网 | 2023-09-16 01:16
目录前言基本概念机器学习的三个基本要素1.模型2.学习准则几种常用的损失函数风险最小化准则3.优化算法参数与超参数梯度下降法前言机器学习就是让计算机从数据中进行自动学习,得到某种知
前言
机器学习就是让计算机从数据中进行自动学习,得到某种知识(或规律),并利用学习到的规律对未知的数据进行预测。整体思路是让计算机“看”大量的样本,并从中学习到一些经验,再用这些经验来识别新的样本。比如进行手写体数字识别的过程。
基本概念
以在市场上买芒果为例,介绍机器学习基本概念。随机挑选一些芒果,列出特征,比如颜色、大小、形状、产地。再列出要预测的标签,比如芒果的甜度、水分(连续值),也可以是离散值比如好、坏。一个标记好特征和标签的芒果就是一个样本,一组样本构成一个数据集,数据集一般分为训练集和测试集,训练集是用来训练模型的,测试集是用来检验模型好坏的。
用一个d维的向量表示一个芒果的所有特征构成的向量,称为特征向量,每一维表示一个特征。假设训练集有N个样本,构成训练集D。
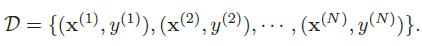
希望让计算机自动学习一个函数来建立每个样本特征向量和标签之间的映射,对于一个未知样本可以通过此函数来预测标签的值。其中 θ是可学习的参数。
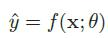
通过一个学习算法,在训练集上找到一组参数θ∗,使得函数f可以近似真实映射关系。这个过程称为学习或者训练过程,函数f称为模型。然后对测试集中的样本使用学习到的模型来预测标签,计算预测结果的准确率。
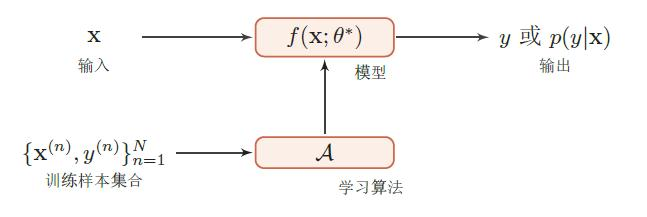
如下图所示为机器学习系统示例:
1.模型
一个机器学习任务需要确定其输入空间和输出空间,不同的机器学习任务的区别主要在于输出空间不同,比如在两类分类问题中y={+1,−1},在C类分类问题中,y={1,2,3...C},在回归问题中y=R。
输入空间和输入空间构成了一个样本空间,对于样本空间中的样本(x,y),要找到一个映射函数g:x−>y,使得y=g(x)。
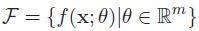
机器学习的目标是找到一个模型来近似真实映射函数g(x)或者真实条件概率分布,于是根据经验确定一个假设函数集合F,称为假设空间,然后观察其在训练集上的效果,选择一个理想的假设f∗∈F,假设空间为一个参数化的函数族,如上式所示,其中,f(x,θ)为假设空间的模型,θ为可学习参数,m为参数数量。常见假设空间分为线性空间和非线性空间,对应的模型分别为线性模型和非线性模型。
线性模型: 线性模型的假设空间为一个参数化的线性函数族,参数θ包括了权重向量W和偏置b。
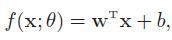
非线性模型: 广义的非线性模型可以理解为多个非线性基函数ϕ(x)的线性组合,即f(x;θ)=wTϕ(x)+b。
令训练集是由N个独立同分布的样本组成,要求样本分布必须是固定的,不会随时间变化,如果本身是可变的,则无法用这些数据学习。一个好的模型f(x,θ∗)应该在所有(x,y) 的可能取值上都与真实映射函数y=g(x)一致,即满足下式。其中ϵ是一个很小的正数。
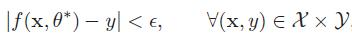
模型f(x;θ)的好坏可以通过期望风险R(θ)来衡量,其中pr(x,y)为真实的数据分布,L(y,f(x;θ))为损失函数,用来量化两个变量之间的差异。
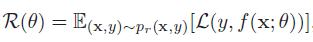
0-1损失函数: 直观表示模型的错误率,但是数学性质不好,不连续且导数为0,难以优化。
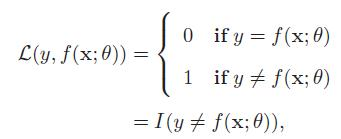
平方损失函数: 一般用在预测标签为实数值的任务中,一般不适用于分类问题。
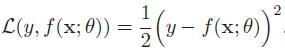
交叉熵损失函数: 一般用于分类问题,假设样本的标签y∈{1,⋅⋅⋅C}为离散的类别,模型f(x;θ)∈[0,1]C的输出为类别标签的条件概率分布,即
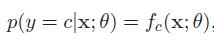
并满足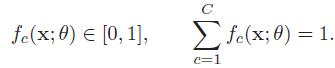
用C维的one-hot向量y表示样本标签,假设样本标签为k,那么只有第k维的值为1,其他为0。可以理解向量y为样本标签的真实概率分布,即样本类别为k,其属于第k类的概率为1,属于其他类的概率为0。对于标签真实分布y和模型预测分布f(x,θ),一般用交叉熵衡量差异,即
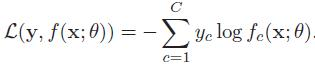
由于y是one-hot向量,所以也可以将交叉熵函数写成如下式所示,其中,fy(x;θ)可以看作真实类别y 的似然函数。因此,交叉熵损失函数也就是负对数似然损失函数。
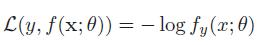
一个好的模型应当有较小的期望错误,但是不知道真实的数据和映射函数,实际上无法计算期望风险R(θ;x,y),只能是通过训练集计算经验风险,也就是训练集上的平均损失。
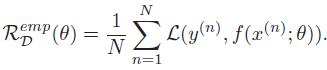
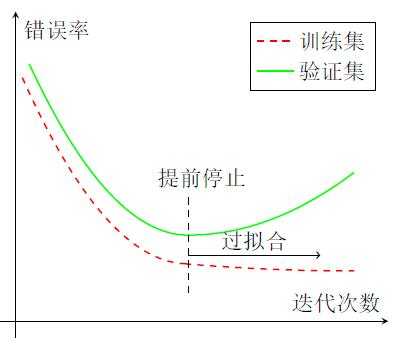
所以学习准则就是找到一组参数θ∗使得经验风险最小,这就是经验风险最小化准则。但是经验风险最小化准则很容易导致模型在训练集上错误率很低,但是在未知数据上错误率很高,这就是过拟合。过拟合问题一般是训练数据少、噪声以及模型能力强造成的。常通过正则化方法,减少参数空间,解决过拟合问题。和过拟合相反的一个概念是欠拟合,即模型不能很好的拟合训练数据,在训练集上错误率就比较高,一般是模型能力不足造成的。
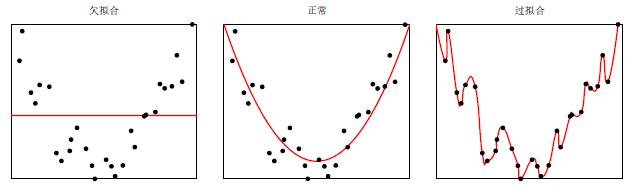
机器学习的训练过程其实就是一个最优化问题的求解过程。
参数与超参数
机器学习优化过程可以分为参数优化和超参数优化,θ是模型的参数,可以通过优化算法学习,这是参数优化过程。还有一类用于定义模型结构或者优化策略的参数,叫做超参数,超参数优化一般根据人的经验来设定,常见的包括聚类算法中的类别个数、梯度下降法的步长、正则项的系数、神经网络的层数、支持向量机中的核函数等。
明确如果一个函数为凸函数,则局部最小解也是全局最小解,目前的算法理论只能确保找到局部最优解,所以很多机器学习方法选择一个凸函数作为优化目标,但也有很多模型的优化目标(比如神经网络)是非凸的,这样只能求解局部最优解。
最常用的优化算法就是梯度下降法,通过迭代来计算风险函数的最小值。α称为学习率。详解: 对于单变量函数,梯度就是微分,代表某个定点的切线的斜率,是变化最快的地方;对于多变量函数,梯度就是各个方向上的微分,指出各个方向上变化最快的方向,也就是整体上函数在给定点上升最快的方向,是一个向量。而梯度下降法过程,就是朝着上升最快方向的反方向前进,直到收敛。
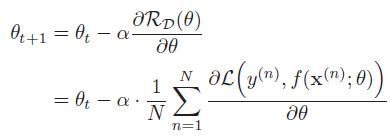
可以通过提前停止防止过拟合,即使用验证集(也叫开发集)进行模型选择,测试模型在验证集上是否最优,如果在验证集上错误率不再下降,就停止迭代。一般对于小数据量的数据集,训练集、验证集、测试集的数据比例为60%、20%、20%,大数据量的比例可以为98%、1%、1%。
传统梯度下降法目标函数是整个训练集,称为批量梯度下降(BGD),每一次迭代需要计算整个训练集样本,耗时长,空间复杂度高。为了减少每次计算复杂度,可以每次只采集一个样本,计算这个样本损失函数的梯度并进行参数更新,即随机梯度下降法(SGD),当经过足够次数的迭代后,也可以收敛到局部最优解。这一方法实现简单,收敛速度快,被广泛应用,相当于在BGD的梯度上引入了随机噪声。

但是SGD不能利用计算机的并行计算能力,效率较低,所以可以使用BGD和SGD的折中,即小批量梯度下降法(Mini-Batch Gradient Descent),每次迭代选取一小部分样本计算梯度并更新参数,提高了训练效率,相对于BGD也引入了少量噪声。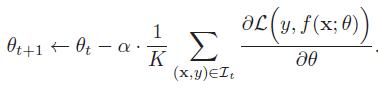
样本子集中包含K个样本,K值的选择一般设置成2的幂次方,可以提高计算效率。