神经网络权重初始化的三种方法

原文链接：https://blog.csdn.net/weixin_41417982/article/details/81507523
在以往的文章里面，全连接层的权重我是给初始化成0的，但卷积层是初始化成正态分布。其实，权重初始化成0是一件很糟糕的事情。

举一个二分类的例子。我们有损失函数L=f−yL=f−y一共两个神经元，每个神经元又是一个两个数值的向量。如图：

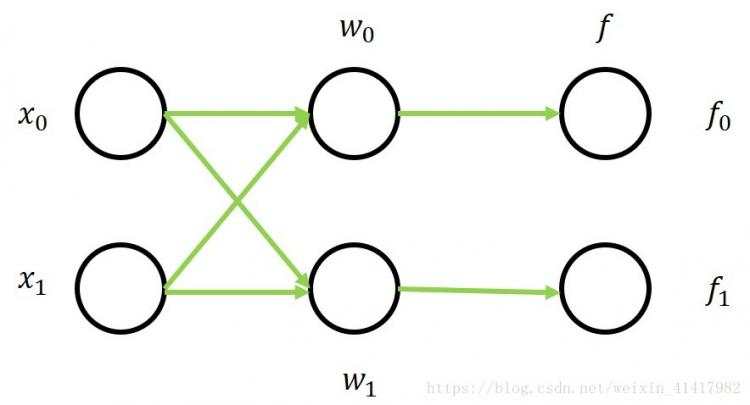
那么问题来了，既然我们都把权重初始化成0，所以w0w0是完全一模一样的，接收的数据也都一样，囊括了所有的数据，那输出也是一样了。根据权重更新的规则，他们得到的更新也都一样。综上，这些神经元其实就是一样的！这也被很多人说是网络对称性的问题。

把这个结论推导到卷积层，自然结果也是一样，所以，把权重初始化为0是一件很笨的事情。为了克服这种现象，我们一般选择随机正态分布初始化权重，但其实还有其他研究人员推出的初始化方法~

PS：当然我用Tensorflow输出每一次的f，发现其实并不一样。后面发现我用的是MSE损失函数，由于求导的问题导致正确分类的求导过程跟其他分类的不同，所以可以更新出不同的权重，最后才能正确识别MNIST数据集。但如果不是损失函数的作用，神经元提取的特征是完全一样的。

一、 随机正态分布初始化

这种方式将权重初始化为固定的均值和方差（例如均值取0，方差取0.01），也是目前应用比较广的一种初始化方式。

CS231n说如果初始的方差小，如0.1，就会导致在前向传播过程中，不同的层的输入不断减小。这会导致很多问题，因为权重的梯度跟输入息息相关。在前面的文章可以看到很多时候ww。那这样子会导致权重的更新速度很慢很慢。

那初始化的方差如果太大呢，就会使得每一层的输出越来越大。形如tanh激活函数，就会容易导致梯度饱和的现象，也自然扑街了。

当然，后面也有更好的初始化方法出来，那就是Xavier。

二、xavier初始化

参考（介绍Xavier）
https://zhuanlan.zhihu.com/p/27919794
https://blog.csdn.net/victoriaw/article/details/73000632

Xavier追求的，就是让我们每一层的输入（也是上一层的输出）都能控制一定范围内，这样就不会在激活函数那一块产生太多的问题，也不会导致梯度太小。

Xavier初始化假设我们的数据（即xx）满足一定的条件。

由于数据和权重相互独立，我们有ff
因为权重的初始化步骤一样，输入的数据也一样，所以下标不同的权重和数据都有确定的方差。因此我们可以把n提出来。

引用第一篇文章里面的原话讲到：

如果样本空间与类别空间的分布差异很大，比如说类别空间特别稠密，样本空间特别稀疏辽阔，那么在类别空间得到的用于反向传播的误差丢给样本空间后简直变得微不足道，也就是会导致模型的训练非常缓慢。同样，如果类别空间特别稀疏，样本空间特别稠密，那么在类别空间算出来的误差丢给样本空间后简直是爆炸般的存在，即导致模型发散震荡，无法收敛。因此，我们要让样本空间与类别空间的分布差异（密度差别）不要太大，也就是要让它们的方差尽可能相等。

为了让我们的Var(f)Var(f)。

我们让权重服从均匀分布，有：

w∼U(a,b)Var(w)=(b−a)2/12=1/nw∼U(a,b)Var(w)=(b−a)2/12=1/n

似乎已经完了，但其实还没有。这只是前向传播的推导，我们把这里的n设为nfnf。

在反向传播中，我们根据前向传播的公式，把激活函数设成σ(x)σ(x)。

由于神经层的在不同传输过程中，权重要取的方差不同，所以取平均数2nf+nb2nf+nb

写了这么多公式，其实有点混乱。或许明天可以再来检查一遍。要提醒的有：

前向传播中，忽略了激活函数。因为输出一旦为确定的方差，那么，经过激活函数的输出也有固定的方差。因为一般使用的激活函数都是以0为中心。至于Relu这种输出不以0为中心的，其实有其他的初始化方法使用，如HE/MSRA。

在反向传播中，损失函数对某一层的梯度等于上一层的梯度乘以自身的梯度。然后不断的从这一层推导到最后一层，就能求出本层梯度与最后一层梯度的关系，是中间所有层的通道数nbnb和权重来决定的。具体推导看不懂也没关系如果你只是想在心里只有这么一个概念的话。

还有一点，反向传播中间推导过程并不是省去了σ′σ′，其实是因为默认它为1。为什么呢？因为回想tanh的函数，在中间部分的函数是接近线性函数的，求导的值为1。假如我们默认输出遵循一定的方差分布，那它映射在损失函数的部位也是中间部分，求导即为1。

三、MSRA

这种方法地提出是为了非常深的神经网络的训练，权重一般被初始化为均值为零，方差为