SIoULoss的原理详解及代码实现分析

paper：SIoU Loss: More Powerful Learning for Bounding Box Regression

code：https://github.com/meituan/YOLOv6/blob/main/yolov6/utils/figure_iou.py#L75 

存在的问题

之前的目标检测模型的回归损失考虑到了预测的bounding box和gt box之间的distance、overlap area、aspect ratio等因素（如GIoU、CIoU等），但是都没有考虑到方向不匹配的问题，这可能会导致收敛速度较慢，因为训练过程中预测的bounding box可能会在gt box附近震荡，最终得到一个较差的模型。

创新点

本文提出了一种新的目标检测损失函数SIoU Loss，其中重新定义了penalty metrics并且考虑到了回归向量的角度。这会让预测的bounding box快速的先移动到最近的坐标轴，随后只需要沿一个方向X或Y回归坐标即可，简而言之，增加角度惩罚项减少了自由度的数量。

方法介绍

SIoU loss一共包括四个惩罚项：

1. Angle cost
2. Distance cost
3. Shape cost
4. IoU cost

Angle cost

如下图所示，定义gt box和predict box中心点连线的夹角 \(\alpha\)，当 \(\alpha <\frac{\pi }{4}\) 时，目标是最小化 \(\alpha\)，当 \(\alpha >\frac{\pi }{4}\) 时，目标是最小化 \(\beta=\frac{\pi}{2}-\alpha\)。

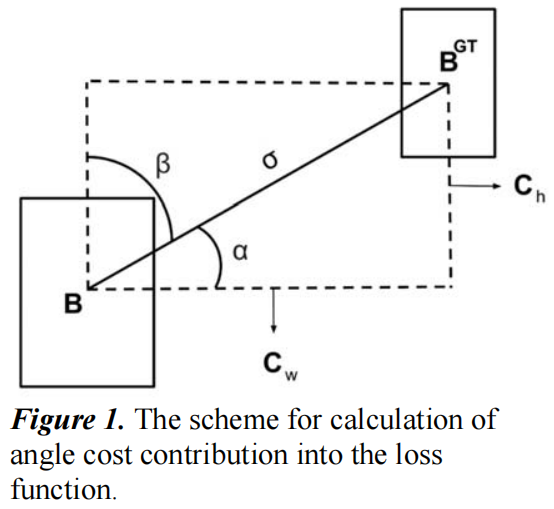
为此，作者提出下式

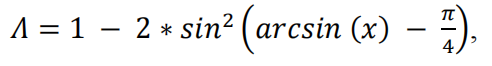
其中

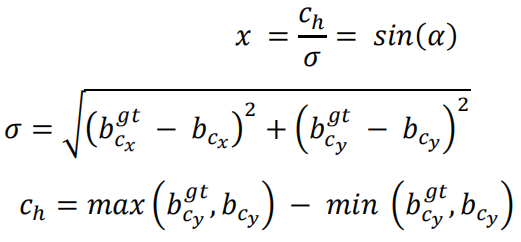
Distance cost

distance cost也被重新设计，加入了上述的angle cost

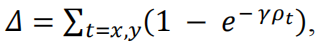
其中

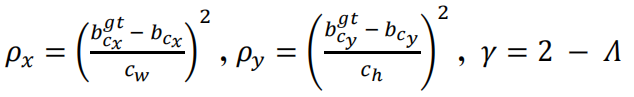
注意，这里的 \(c_w,c_h\) 和angle cost中的不一样，不然的话这里 \(\rho_x=\rho_y=1\) 了。angle cost中的是predict box和gt box中心点沿 \(x,y\) 方向的距离，这里的是两者最小外接矩形的宽和高，如下图所示

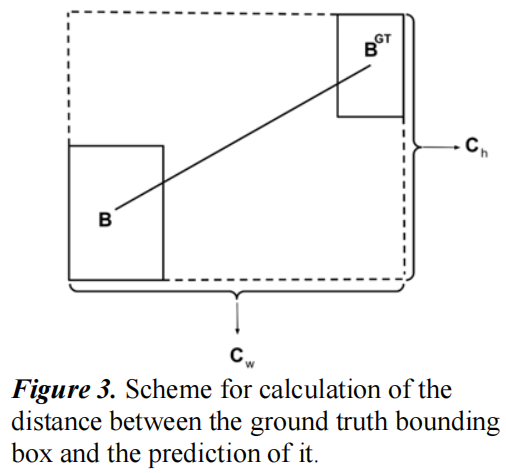
Shape cost

shape cost的定义如下

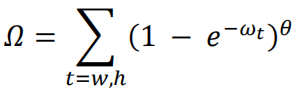
其中

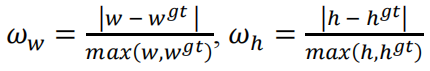
其中 \(\theta\) 值定义了shape cost的权重并且不同的数据集 \(\theta\) 值也不同。

SIoU loss的最终形式如下

其中

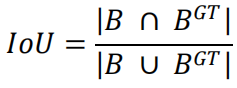
代码

下面是YOLOv6中实现的SIoU loss，其中计算angle_cost是对论文中的式子进行了转换，如下

s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5 + self.eps
s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5 + self.eps
sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)
sin_alpha_1 = torch.abs(s_cw) / sigma
sin_alpha_2 = torch.abs(s_ch) / sigma
threshold = pow(2, 0.5) / 2
sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)
rho_x = (s_cw / cw) ** 2
rho_y = (s_ch / ch) ** 2
gamma = angle_cost - 2
distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)
omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
iou = iou - 0.5 * (distance_cost + shape_cost)
loss = 1.0 - iou

实验结果

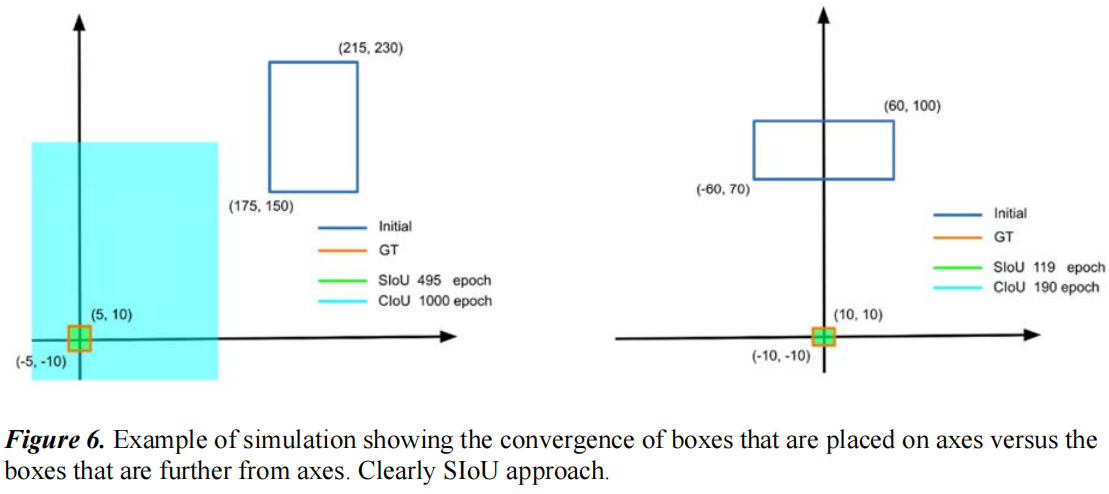
下图是一个简单的实验用于比较anchor初始位置不同时SIoU和CIoU的收敛速度，其中蓝色box是anchor的初始位置，位于原点的绿色box是target box，可以看出，当anchor初始位置和目标box在同一轴上时，收敛速度要比不在同一轴上快的多。而两种情况下SIoU的收敛速度都比CIoU快。

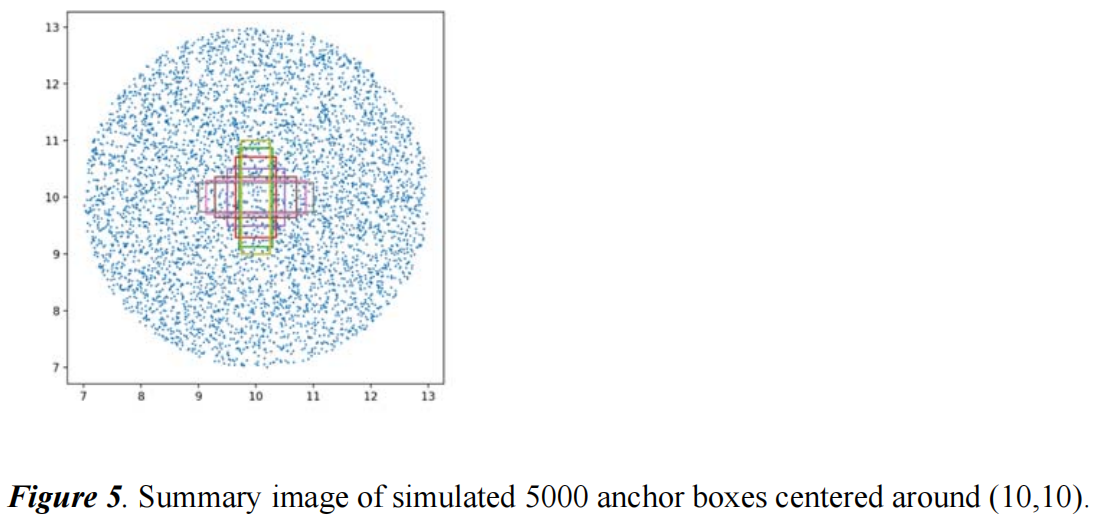
作者又用了CIoU里设计的模拟实验来评估SIoU的效果，实验具体设计为：7个中心在坐标(10,10)处，面积为1，宽高比分别为1:4, 1:3, 1:2, 1:1, 2:1, 3:1, 4:1的box作为target box，如下图中(10,10)处的各色box所示。anchor box均匀的放置在以坐标(10,10)为中心半径为3的区域内的5000个点上，即下图中的蓝色点。每个点放置7种尺度7种宽高比共49个anchor，尺度分别为0.5, 0.67, 0.75, 1.33, 1.5, 2，宽高比和target box的一致。因此一共有5000x7x7=1715000个回归实例。

下图是实验结果，可以看出SIoU的最大误差要比CIoU小了两个数量级，并且SIoU的误差表面更加平滑，表明在模拟的所有情况下，SIoU的总误差都比CIoU小。

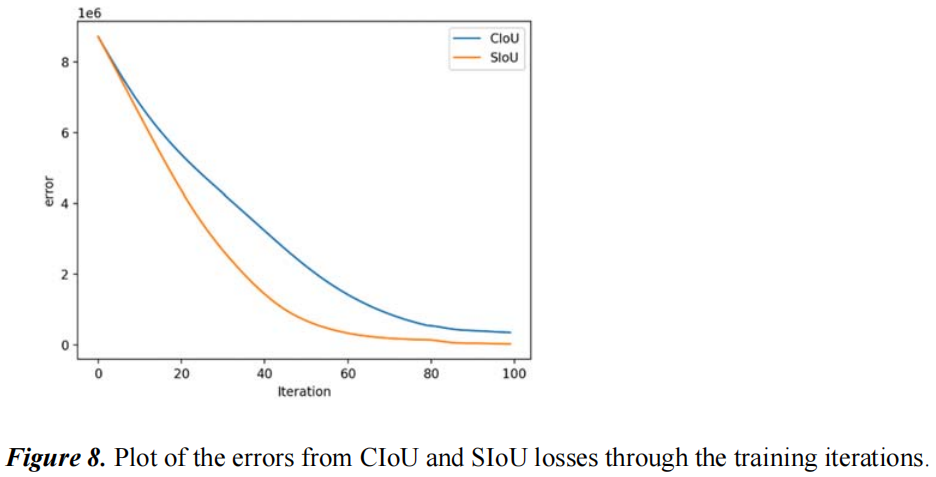
下图是误差随迭代次数的变化，可以看出SIoU比CIoU的收敛速度更快，最终的误差也更小。

参考

一文搞懂EIoU与SIoU - 知乎