如何用人工神经网络处理决策边界问题？这里有一份简单的代码参考

从本质上说，人工神经网络（ANN）是一种信息处理的范式，它受到人脑信息处理流程的启发，目前在机器学习领域得到了非常广泛的应用。

然而，可能许多人并不知道的是，ANN 早在 40 年代就被提出了。在最初的那几年，ANN 曾在一定程度上引起了业界的关注，但由于那时没有当前强大的硬件运算能力和高效的模型训练算法，因此ANN很快就销声匿迹了。但随着时代的进步，技术的发展，目前 ANN 几乎成了人工智能的代名词，特别是随着自动编码器、卷积网络、Dropout 正则化（dropout regularization）和其他各种技术的出现，ANN 的性能表现得到了显著提升。

医学研究表明：人脑的神经网络由神经元组成，它们通过神经突触相互连接，传输信号。一般情况下，只有当一个神经元接收的信号量超过某一阈值，它才会向与之相连的其他神经元传输这一信号。而且，人脑的神经网络可以在任何神经元之间建立连接关系，甚至自己和自己连接。如果完全照搬人脑的这种链接结构，那么人工神经网络将很难训练，因此在大部分的实际应用场景中，研究者们通常会对人工神经网络做出一些精简和限制（例如不能自己和自己连接等）。

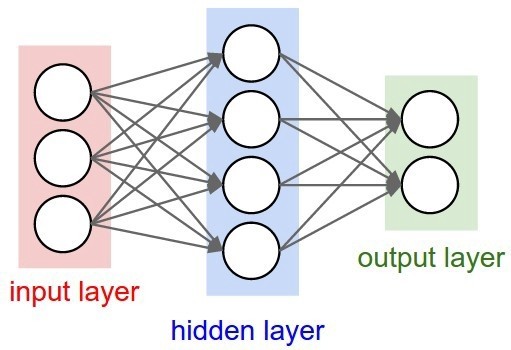
在多层感知机（multi-layer perceptron）的情况下，神经元会被按层排列，并且每个神经元只能向下一层的神经元发送信号。第一层由输入数据组成，最后一层输出最终的预测值，称为输出层。这里所有的神经元都通过所谓的突触（synapse）连接。

与人脑神经网络传输信号时的阈值相对应，在 ANN 中通常会使用 Sigmoid 函数来计算神经元的输出。函数图像和表达式如下所示。

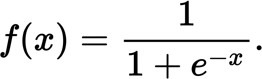
一般情况下，ANN 的训练过程大概可以分为如下两个阶段：

1. 前向传递，数据从输入经过 ANN 流向输出，被称为前馈（feed forward）。

2. 反向传递，从输出端开始，计算每个神经元的误差，然后根据计算结果调整网络权重，被称为反向传播（Backpropagation）。

下文中，我们将首先尝试用传统的逻辑回归算法来处理决策边界问题，接着引入 ANN，通过对比我们将看到 ANN 的强大。需要说明的是，这里我们只实现了一个简单的三层 ANN 结构（即上图中的 hidden layer 有 3 层），并且，我们省略了一些数学和机器学习的基础知识介绍，包括分类、正则化和梯度下降等。另外，我们还采用了一些基于 Python 的现成的机器学习库。

逻辑回归

我们首先用逻辑回归的方法处理决策边界问题，即训练一个逻辑回归分类器。这里分类器的输入是来自数据集的x值或y值，输出是我们的预测分类结果（在本例中就是0或1，分别代表红色和蓝色两种颜色）。

下面的代码声明了我们所需要的支持库。

# Package imports 

import matplotlib.pyplot as plt 

import numpy as np 

import sklearn 

import sklearn.datasets 

import sklearn.linear_model 

import matplotlib

下面的代码用随机数的方法生成了需要进行边界决策的数据集。

# Generate a dataset and plot it

np.random.seed(0)

X, y = sklearn.datasets.make_moons(200, noise=0.20)

plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)

plt.show()

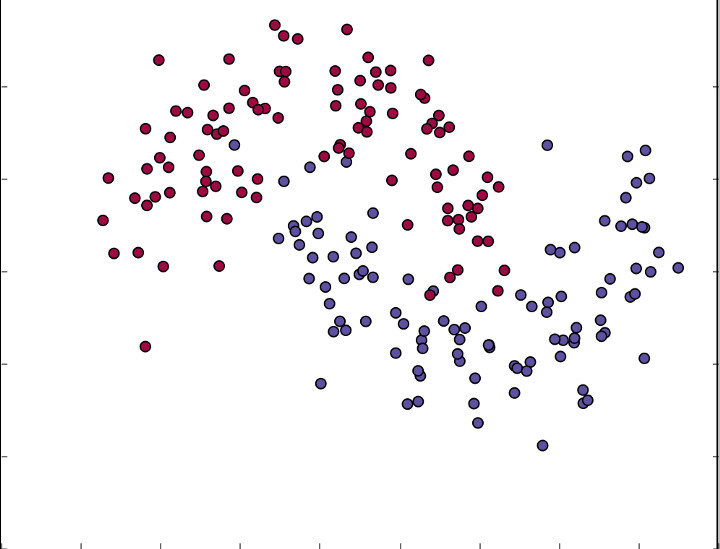
根据数据集绘制的点状分布图如下所示。

在scikit-learn库的帮助下，我们用此数据训练逻辑回归分类器，代码如下。

# Train the logistic regression classifier

clf = sklearn.linear_model.LogisticRegressionCV()

clf.fit(X, y)

# Plot the decision boundary (the method is in the main code link provided in the end)

plot_decision_boundary(lambda x: clf.predict(x))

plt.title("Logistic Regression")

最终的输出结果如下。

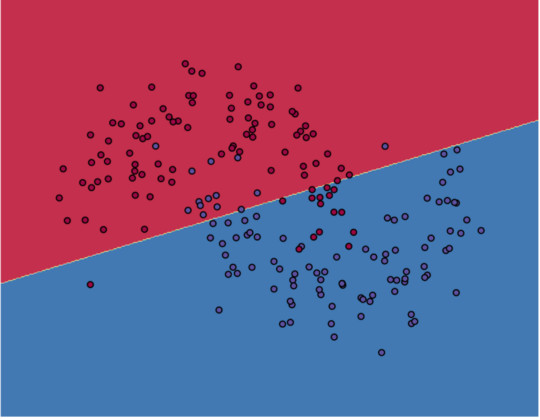
可以看到，逻辑回归分类器用直线将数据分为红、蓝两类，虽然结果已经相当令人满意了（可以看到绝大部分的红、蓝色点已经被分开了），但如果我们想要得到更精准的结果（即完全把红、蓝色点分开），显然需要借助更强大的解决方案，也就是下文即将实现的 ANN。

人工神经网络

下面我们构建一个三层 ANN 来解决该问题，看看结果和逻辑回归相比有何不同。

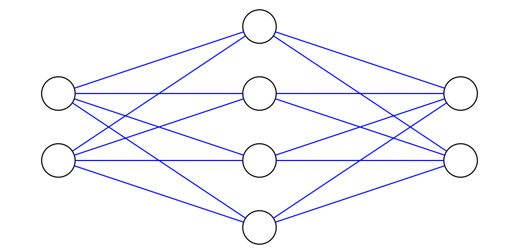
首先是关于隐藏层（hidden layer）维度（即节点数量）的选择，一般认为更多的节点，就能实现更加复杂的函数。但高维度在模型训练和结果预测时又需要巨大的计算能力支撑，而且大量的参数还可能造成过拟合（overfitting）问题。因此，如何选择隐藏层的维度大小，还是要取决于具体的待解问题，而且它更多的是一门艺术而并非科学。下文我们将看到隐藏层的维度如何影响 ANN 的输出，这里首先给出几条最基础的 ANN 维度规则。

1. ANN 通常都会具有一个输入层，一个隐藏层和一个输出层。

2. 输入层的节点数量由输入数据的维度决定。

3. 输出层的节点数量由输出类别的数量决定。（本例中输出层的维度是2，因为我们只有0和1两种结果）。

下面我们还需要为隐藏层选择一个激活函数（activation function）。激活函数负责将某一层的输入转换为输出，一般非线性函数用于拟合非线性的假设。激活函数最常见的选择包括：双曲正切函数（tanh），Sigmoid 函数和 ReLu（Rectified Linear Units）函数等。本例中采用的是双曲正切函数 tanh。

因为我们想要的最终结果是概率，因此输出层的激活函数选择 Softmax 函数会比较合适，这是一个将原始的数字结果转换为概率的最简单的方法。这里可以将 Softmax 函数视为 Logistic 函数对多个分类的泛化（generalization）。

ANN如何进行预测？

如上文所述，整个训练大概可以分为两个过程。一是前向传递，即训练数据从输入端流向输出，得到最终的预测值，这是一个前馈过程。二是反向传递，即通过参数学习（learning the parameters），找到一组最合适的参数组合，使得 ANN 的训练误差最小化。我们一般将测量误差的函数称为损失函数（loss function），由于上文我们将 Softmax 函数作为输出层的激活函数，因此按照一般的习惯，这里将 cross-entropy loss（交叉熵损失函数）作为损失函数。

ANN的实现

首先我们为后续的梯度下降过程定义一些变量和参数，代码如下。

num_examples = len(X) # the training set size

nn_input_dim = 2 # dimension of the input layer

nn_output_dim = 2 # dimension of the output layer

# Gradient descent parameters

epsilon = 0.01 # the learning rate for gradient descent

reg_lambda = 0.01 # the strength of regularization

接着定义损失函数。

def calculate_loss(model):

定义辅助函数（helper function）预测输出结果（0或1）。

def predict(model, x):

最后，我们定义 ANN 的训练函数，它使用上面定义的反向传播导数实现批量梯度下降（batch gradient descent）。

def build_model(nn_hdim, num_passes=20000, print_loss=False):

ANN的预测结果

下面我们用上文提到的点状数据对 ANN 展开训练。

# Build a model with a 3-dimensional hidden layer

model = build_model(3, print_loss=True)

# Plot the decision boundary

plot_decision_boundary(lambda x: predict(model, x))

plt.title("Decision Boundary for hidden layer size 3")

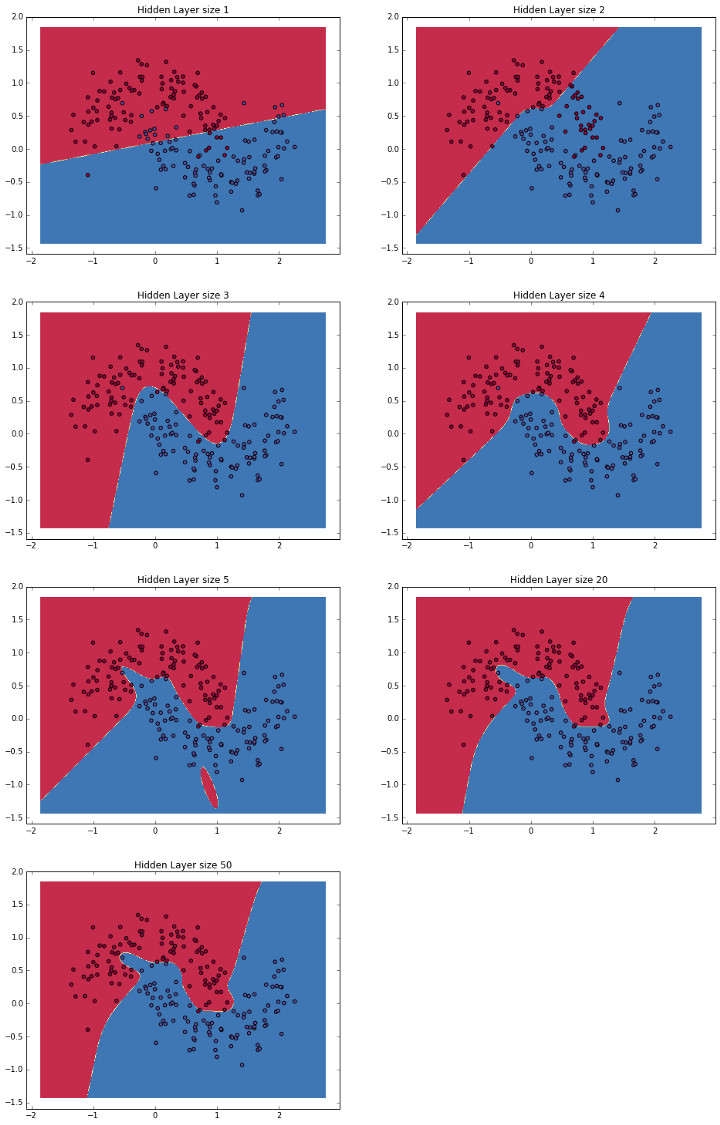
从以上结果可以看到，随着训练次数的增多，模型的预测结果也就越好。低维的隐藏层可以很好地捕获数据的总体趋势，而更高的维度可能会因为记忆效应而产生过拟合，但是其总体形状还是正确的。如果我们要在其他的数据集上对模型进行测试，那么隐藏层维度更小的模型可能会得到更好的效果，因为它们泛化的更好。另外，虽然可以采用更强的正则化来抵消高维度引起的过拟合，但选择一个合适的隐藏层维度则是更为经济的方案。

完整源代码：https://github.com/NSAryan12/nn-from-scratch/blob/master/nn-from-scratch.ipynb

来源：medium，雷锋网(公众号：雷锋网)编译，雷锋网版权文章

雷锋网相关阅读：

Google软件工程师解读：深度学习的activation function哪家强？

MIT重磅研究：基于人工神经网络，探索抑制神经元的生物学意义

如何对神经网络人工智能硬件进行优化设计？

雷锋网版权文章，未经授权禁止转载。详情见。