对于齐次变换矩阵之间的相乘,我们以三个坐标系之间的变换关系为例:
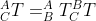
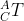 是{C}在{A}中的描述,
是{C}在{A}中的描述,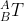 是{B}在{A}中的描述,
是{B}在{A}中的描述,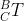 是{C}在{B}中的描述。
是{C}在{B}中的描述。
对于坐标系之间的运动过程,我们可以做如下两种理解:
(1)从右往左乘
第一步:{C}相对于{A}或者说是{B}做变换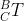 ;
;
第二步:{B}{C}再一起(固接)相对{A}系做变换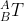
物理意义:相对固定坐标系先后发生的若干运动合成(从右往左乘)
(2)从左往右乘
第一步:{B}{C}一起相对B系作运动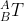 ;
;
第二步:{C}再相对于{B}系作运动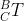 。
。
物理意义:相对运动坐标系先后发生的若干运动系得合成(从左向右乘)
在这里,我们对一个目标位置,使用两种运动不同得先后运动顺序来获得,也就说已知目标位置的情况下,我们逆向推导运动顺序。
若我们已知运动的先后作用次序,那么我们就只能使用(1)或者(2)中的一种矩阵相乘顺序来获得最终位置。
此部分参考
1.东南大学-机器人原理
2.燕山大学-机器人技术

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有