Python科学计算Scipy

常用包

1.1 常数包

from scipy import constants as C


1.2 特殊函数包

四舍五入&＃xff1a;scipy与numpy有些不同

具体使用&＃xff1a;help(special)查看更多使用方法

2.1 理论基础

简单线性回归

在统计学中&＃xff0c;线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。一个带有一个自变量的线性回归方程代表一条直线。我们需要对线性回归结果进行统计分析。

最小二乘法&＃xff08;又称最小平方法&＃xff09;是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据&＃xff0c;并使得这些求得的数据与实际数据之间误差的平方和为最小

• 最优化问题
  
  
• 最小二乘法

通过求导来确定最小值
这里的未知数是a,b

2.2 ⭐最小二乘法(leastsq)

• 可视化
  
  

2.3 函数最小值(fmin)

求偏差函数最小值

• 函数最小值
  
  
  
  
  
• 梯度下降法

类似于走山坡&＃xff1a;若你发现你往上走则掉头往下&＃xff1b;反之&＃xff0c;若是往下走&＃xff0c;则继续走
此外还有牛顿法、共轭下降法[抽象不懂&＃xff0c;不在此展开陈述]

2.4 非线性方程组求解(fsolve)

2.5 实现最小二乘法

2.6 实现梯度下降法

拟合 插值&＃xff1a;都是想得到某种模型的特性曲线
拟合不要求通过所有点&＃xff0c;样本数据量比较大的时候
插值要求必须过所有点&＃xff0c;适合数量比较少的时候&＃xff0c;同时我们暂时还不知道用什么曲线去拟合
现在所讲插值只能对样本数据点中间的值进行插值&＃xff1a;例如 原始数据0-10 只能对0-10之间进行插值

• 二维插值
  
  
  

4.1 线性代数

SciPy.linalg与NumPy.linalg
scipy.linalg包含numpy.linalg中的所有函数。 另外&＃xff0c;scipy.linalg还有一些不在numpy.linalg中的高级函数。 在numpy.linalg上使用scipy.linalg的另一个优点是它总是用BLAS/LAPACK支持编译&＃xff0c;而对于NumPy&＃xff0c;这是可选的。 因此&＃xff0c;根据NumPy的安装方式&＃xff0c;SciPy版本可能会更快。//原文出自【易百教程】&＃xff0c;商业转载请联系作者获得授权&＃xff0c;非商业请保留原文链接&＃xff1a;https://www.yiibai.com/scipy/scipy_linalg.html
点击跳转

from scipy import linalg
import numpy as np


• ⭐svd分解

• 图像压缩
• 噪声消除

• 奇异矩阵

奇异矩阵是线性代数的概念&＃xff0c;就是该矩阵的秩不是满秩。
首先&＃xff0c;看这个矩阵是不是方阵(即行数和列数相等的矩阵&＃xff0c;若行数和列数不相等&＃xff0c;那就谈不上奇异矩阵和非奇异矩阵)。然后&＃xff0c;再看此矩阵的行列式|A|是否等于0&＃xff0c;若等于0&＃xff0c;称矩阵A为奇异矩阵;若不等于0&＃xff0c;称矩阵A为非奇异矩阵。 同时&＃xff0c;由|A|≠0可知矩阵A可逆&＃xff0c;这样可以得出另外一个重要结论:可逆矩阵就是非奇异矩阵&＃xff0c;非奇异矩阵也是可逆矩阵。 如果A为奇异矩阵&＃xff0c;则AX&＃61;0有无穷解&＃xff0c;AX&＃61;b有无穷解或者无解。如果A为非奇异矩阵&＃xff0c;则AX&＃61;0有且只有唯一零解&＃xff0c;AX&＃61;b有唯一解。

• 正交矩阵
  
  
• 对角矩阵

对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵&＃xff0c;常写为diag&＃xff08;a1&＃xff0c;a2,…,an) 。对角矩阵可以认为是矩阵中最简单的一种&＃xff0c;值得一提的是&＃xff1a;对角线上的元素可以为 0 或其他值&＃xff0c;对角线上元素相等的对角矩阵称为数量矩阵&＃xff1b;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算&＃xff0c;且结果仍为对角阵。

4.1.1 噪声消除

4.2 数值积分

• 一维
  
• 二维
  
  

4.3 ⭐实战-svd分解对图像压缩

进行svd的图像的shape是不变的&＃xff0c;但是为什么可以压缩呢&＃xff1f;
是PNG这种图片格式进行压缩
png图片压缩原理解析
【数据压缩】LZ77算法原理及实现

• 导入库
  

misc模块&＃xff0c;提供一些基本的图像相关的读写函数&＃xff0c;可以很轻松的读取本地图像文件到Python程序里&＃xff0c;也可将数据输出到图像文件。misc模块自带一些灰度图像ascent和彩色的face图&＃xff0c;可以scipy.misc.ascent()直接获取爬楼梯ascent图数据到Python程序里&＃xff0c;用scipy.misc.face()获取一副 raccoon浣熊face图&＃xff0c;这两个函数的返回值都是Numpy的ndarray数组。 face图像是个彩色图像&＃xff0c;其数据是个三维数组&＃xff0c;是个1024x768的图像&＃xff0c;而图像中每个像素的值又是一个数组&＃xff0c;分别对应该像素颜色的红、绿、蓝分量。ascent图像是个灰度图像&＃xff0c;其数据是个二维数组&＃xff0c;分别对应图像中每个像素的灰度值。

• svd分解
  

# 原始图像
plt.gray()
# subplot是将多个图画到一个平面上的工具
# 221 两行两列 第一张图
plt.subplot(221,aspect&＃61;&＃39;equal&＃39;)
plt.title(&＃39;orignal&＃39;)
plt.imshow(gray)
plt.imsave(&＃39;org.png&＃39;,gray) #保存# 取奇异特征值前10个主成分压缩的图像
A &＃61; np.dot(U[:,:10],np.dot(np.diag(s[:10]),Vh[:10,:]))
plt.subplot(222,aspect&＃61;&＃39;equal&＃39;)
plt.title(&＃39;:10&＃39;)
plt.imshow(A)
plt.imsave(&＃39;a10.png&＃39;,A) #将压缩后的数组保存为PNG格式# 取前50个主成分压缩的图像
B &＃61; np.dot(U[:,:50],np.dot(np.diag(s[:50]),Vh[:50,:]))
plt.subplot(223,aspect&＃61;&＃39;equal&＃39;)
plt.title(&＃39;:50&＃39;)
plt.imshow(B)
plt.imsave(&＃39;b50.png&＃39;,B) #将压缩后的数组保存为PNG格式# 取前100个主成分压缩的图像
C &＃61; np.dot(U[:,:100],np.dot(np.diag(s[:100]),Vh[:100,:]))
plt.subplot(224,aspect&＃61;&＃39;equal&＃39;)
plt.title(&＃39;:100&＃39;)
plt.imshow(C)
plt.imsave(&＃39;c100.png&＃39;,C) #将压缩后的数组保存为PNG格式 plt.show()# png格式是无损压缩


**subplot&＃xff08;m,n,p&＃xff09;**或者subplot&＃xff08;mnp&＃xff09;此函数最常用&＃xff1a;subplot是将多个图画到一个平面上的工具。其中&＃xff0c;m表示是图排成m行&＃xff0c;n表示图排成n列&＃xff0c;也就是整个figure中有n个图是排成一行的&＃xff0c;一共m行&＃xff0c;如果第一个数字是2就是表示2行图。p是指你现在要把曲线画到figure中哪个图上&＃xff0c;最后一个如果是1表示是从左到右第一个位置。 &＃xff09;

• 效果展示 无损压缩
  
  
  

5.1 信号处理

设计滤波器&＃xff0c;怎样从噪声中&＃xff0c;拿到真正的信号

• 理想信号
  

真实的测量基本不会是理想的信号&＃xff0c;难免会有噪声的出现

• 加入噪声
  

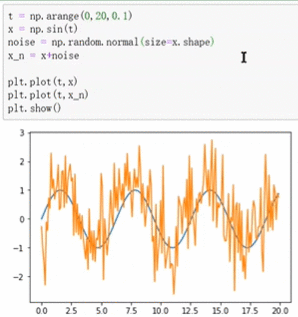
噪声过大&＃xff0c;导致原始噪声无法辨别

• 调整噪声
  

噪声来源&＃xff1a;传感器测量、环境、温度、震动等

我们要做的是将噪声弱化&＃xff0c;恢复到平滑的

• 中值滤波器 低通滤波器
  
• • 奇数太大&＃xff1a;

选取合适的数值

• 对原始清晰的图像进行中值滤波会使图像变模糊
  
  
• 对原始清晰的图像加上噪声 再进行中值滤波
  

5.2 傅里叶变换

周期的方波信号可以由无限个奇次信号叠加生成

• 实例
  

时域图 --> FFT --> 频域图
振幅、周期、相移和频率

• 实例 分析复杂信号
  
  

>>> from numpy import *
>>> a1 &＃61; [[1,2,3],[4,5,6]] #列表
>>> a2 &＃61; array(a1) #a2数组
>>> a2
array([[1, 2, 3],[4, 5, 6]])
# mat&＃xff08;&＃xff09;函数将目标数据的类型转化成矩阵&＃xff08;matrix&＃xff09;
>>> a3 &＃61; mat(a1) #矩阵
>>> a3
matrix([[1, 2, 3],[4, 5, 6]])
>>> a4 &＃61; a2.tolist()
>>> a4
[[1, 2, 3], [4, 5, 6]]
>>> a5 &＃61; a3.tolist()
>>> a5
[[1, 2, 3], [4, 5, 6]]
>>> a4 &＃61;&＃61; a5
True


问题&＃xff1a;
解决&＃xff1a;