排序算法专题归并排序

  归并排序是一种十分经典的冲破O(n²)时间复杂度的排序算法&＃xff0c;该算法是基于分治的思想&＃xff0c;讲解算法原理之前&＃xff0c;先看一下下面这张图。

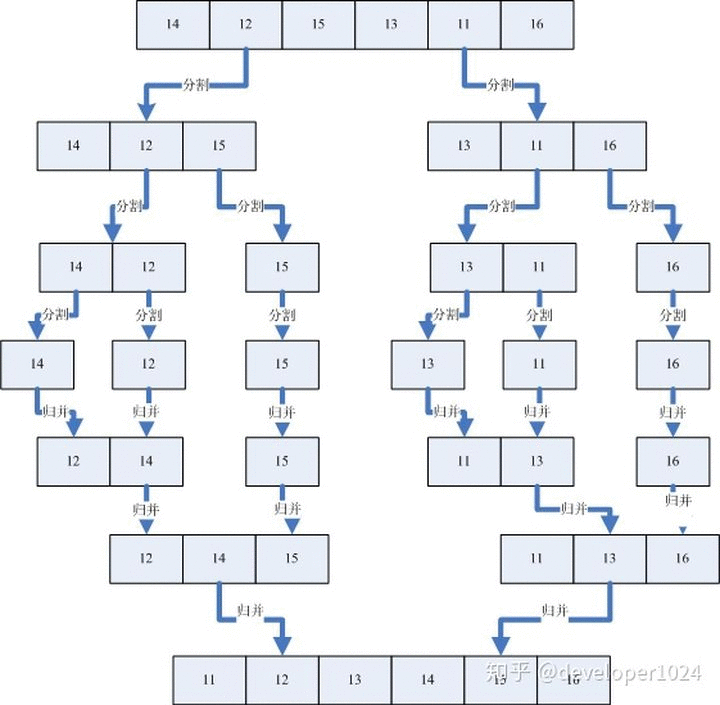
• 图片来源&＃xff1a;【算法】排序算法之归并排序
    上图就是归并算法的一个简单示例。该算法就是每次将数组递归拆解为两部分&＃xff0c;直到所有部分包含元素为1&＃xff0c;之后递归的将各个部分进行归并。
• 具体的算法步骤如下&＃xff1a;

• 1:递归拆解数组&＃xff0c;直到每个区块包含元素数量为1
  2&＃xff1a;归并数组&＃xff0c;直到归并后的数组长度等于原数组长度
  3&＃xff1a; 申请空间&＃xff0c;使其大小为两个已经排序序列之和&＃xff0c;该空间用来存放合并后的序列
  4&＃xff1a;设定两个指针&＃xff0c;最初位置分别为两个已经排序序列的起始位置
  5&＃xff1a;比较两个指针所指向的元素&＃xff0c;选择相对小的元素放入到合并空间&＃xff0c;并移动指针到下一位置
  5&＃xff1a;重复步骤 4直到某一指针达到序列尾
  7&＃xff1a;将另一序列剩下的所有元素直接复制到合并序列尾
  8&＃xff1a;重复步骤2-7

  从上述可以看出&＃xff0c;该算法的实现是基于递归思想&＃xff0c;但是所有的递归都可以转换成迭代&＃xff0c;因此该算法有两个实现方式&＃xff0c;递归和迭代。

• 代码如下&＃xff0c;以递归为例&＃xff1a;
• 如果单从原理原理上来直接写代码会比较复杂&＃xff0c;我们可以将该算法拆解为两个部分&＃xff0c;及分割和归并。分割是一个简单的递归&＃xff0c;代码如下&＃xff1a;

def mergeSort(nums):"""将输入数组递归拆分&＃xff0c;直到长度为1时返回&＃xff0c;对每一步返回的left,right进行顺序归并>>>mergeSort(3,38, 5, 44, 15, 36)>>>[3, 5, 15, 36, 38, 44]"""if len(nums) < 2:return numsmid &＃61; len(nums)//2left, right &＃61; nums[:mid], nums[mid:]return mergeHelp(mergeSort(left), mergeSort(right))


• 其中mergeHelp是mergeSort的一个help方法&＃xff0c;用于对拆分后的数组进行顺序归并。
• 以[3,38, 5, 44, 15, 36]举个栗子&＃xff0c;说一下递归过程&＃xff1a;

• 1&＃xff1a;[3, 38, 5] [44, 15, 36]
  2&＃xff1a;[3] [38, 5]
  3&＃xff1a;[38] [5]
  4&＃xff1a;[44] [15, 36]
  5&＃xff1a;[15] [36]

• 接下来我们实现mergeHelp方法&＃xff0c;就是给定两个有序数组&＃xff0c;将其按顺序合并为一个数组&＃xff0c;代码如下&＃xff1a;

def mergeHelp(left, right):"""归并排序的help方法&＃xff0c;用于将拆分的left和right进行顺序归并>>>mergeHelp([1, 3, 5], [2, 4, 5]):>>>[1, 2, 3, 4, 5, 5]"""res &＃61; []while left and right:if left[0] <&＃61; right[0]:res.append(left.pop(0))else:res.append(right.pop(0))while left:res.append(left.pop(0))while right:res.append(right.pop(0))return res


• 当我们实现了这个方法之后&＃xff0c;看一下分割&＃43;归并的过程

• [3, 38, 5] [44, 15, 36]  第一次分割
  左数组[3, 38, 5]部分&＃xff1a;
  [3] [38, 5]  第一次分割
  [38] [5]  第二次分割&＃xff08;左数组分割完毕&＃xff0c;所有部分元素均为1&＃xff09;
  [5, 38]  第一次归并
  [3, 5, 38]emsp; 第二次归并&＃xff0c;完成[3, 38, 5]部分序列的排序
  右数组[44, 15, 36]部分&＃xff1a;
  [44] [15, 36]  第一次分割
  [15] [36]  第二次分割
  [15, 36]  第一次合并
  [15, 36, 44]  第二次合并
  原数组的所有子序列完成排序&＃xff0c;进行最终的合并
  [3, 5, 15, 36, 38, 44]  排序完成

• 算法解析&＃xff1a;算法的时间复杂度从两个部分分来来看&＃xff0c;很明显在mergeSort()递归方法里面&＃xff0c;迭代公式为mid &＃61; len(nums)//2&＃xff0c;该方法的时间复杂度是O(log n)&＃xff0c;而在mergeHelp()归并方法里面&＃xff0c;每一步像res里面追加一下元素&＃xff0c;最终的的运行次数为len(left)&＃43;len(right)&＃xff0c;很明显时间复杂度为O(n)&＃xff0c;因此归并排序算法的总时间复杂度为O(n log n)。由于算法运行过程中&＃xff0c;会递归生成原数组的切片&＃xff0c;切片总长度为n&＃xff0c;所以归并排序算法的空间复杂度为O(n)。
• 注意到我们在进行归并操作是&＃xff0c;使用的是如下代码

while left and right:if left[0] <&＃61; right[0]:res.append(left.pop(0))else:res.append(right.pop(0))


• 也就是说对于同样大小的元素&＃xff0c;我们先插入位于左边的&＃xff0c;而后插入右边的&＃xff0c;因此归并排序不会改变相同元素的相对位置&＃xff0c;因此该算法是稳定的。