所谓的经典乘法就是在小学的时候学到的那一套做乘法的方法。如果假设被乘数a和乘数b为:
, 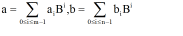 …………(1.1)
…………(1.1)
则经典乘法是这样做的:
。 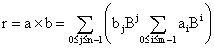 …………(1.2)
…………(1.2)
即分别做a×bi,再累加到r上。
算法如下:(参见[1]算法14.12)
───────────────────────────────────────
算法: 经典乘法
step1: 对i从0到(m+n-1),令ri←0。
step2: 对j从0到n-1,执行如下运算:
2.1) c←0。
2.2) 对于i从0到m-1,
2.2.1) 计算 
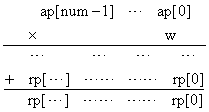
| |  …………(1.3) …………(1.3)
这里的h32表示h为32比特,h16表示h为16比特,其余同理。 说明(2)、(3)可归纳为下表: | 函数名称 | 数学表达式 | 调用情况 | | mul (r, a, bl, bh, c ) | 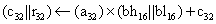
| 
| 
| 最底层 |
表1.2 bn_mul、bn_mul_add与mul64的比较 关于上述函数与宏定义的关系请参见§1.2.3。 当乘数退化成一个字的时候,可以使用大整数与字的乘法。 ─────────────────────────────────────── BN_ULONG bn_mul_word(BIGNUM *a, BN_ULONG w) 功能: 大数与字的乘法 输入: a【大数】,w【字】 输出: a←a×w 返回: 1【正常】 or 0【出错】 出处: bn_word.c ─────────────────────────────────────── 注意:这个函数的名称bn_mul_word和前面提到的bn_mul_words(见本小节对经典乘法函数bn_mul_normal的说明(1))很相似,功能也有些相似,都可以看作是做大整数(前者对应BIGNUM *而后者对应BN_ULONG *)与字的乘法。bn_mul_word(a,w)是做大整数与字的乘法a←a×w,而bn_mul_words 主要是被乘法运算调用,作为一个内部子函数来调用,基本上没有作为独立的函数在用。请注意区别。
推荐阅读
-
本文详细介绍了如何在ARM架构的目标设备上部署SSH服务端,包括必要的软件包下载、交叉编译过程以及最终的服务配置与测试。适合嵌入式开发人员和系统集成工程师参考。 ...
[详细]
蜡笔小新 2024-11-20 14:13:38
-
本文探讨了线性Kalman滤波器(LKF)在不同自由度(2、4、7)的车辆悬架系统中进行主动控制的应用。通过详细的仿真分析,展示了LKF在提升悬架性能方面的潜力,并总结了调参过程中的关键要点。 ...
[详细]
蜡笔小新 2024-12-27 20:47:55
-
-
1:有如下一段程序:packagea.b.c;publicclassTest{privatestaticinti0;publicintgetNext(){return ...
[详细]
蜡笔小新 2024-12-27 19:32:17
-
本文详细介绍了七种经典的排序算法及其性能分析。每种算法的平均、最坏和最好情况的时间复杂度、辅助空间需求以及稳定性都被列出,帮助读者全面了解这些排序方法的特点。 ...
[详细]
蜡笔小新 2024-12-27 19:25:14
-
本文介绍如何利用动态规划算法解决经典的0-1背包问题。通过具体实例和代码实现,详细解释了在给定容量的背包中选择若干物品以最大化总价值的过程。 ...
[详细]
蜡笔小新 2024-12-27 19:17:15
-
本文详细探讨了Java中的24种设计模式及其应用,并介绍了七大面向对象设计原则。通过创建型、结构型和行为型模式的分类,帮助开发者更好地理解和应用这些模式,提升代码质量和可维护性。 ...
[详细]
蜡笔小新 2024-12-27 19:10:10
-
本文介绍了Java并发库中的阻塞队列(BlockingQueue)及其典型应用场景。通过具体实例,展示了如何利用LinkedBlockingQueue实现线程间高效、安全的数据传递,并结合线程池和原子类优化性能。 ...
[详细]
蜡笔小新 2024-12-27 18:51:49
-
题目描述:给定n个半开区间[a, b),要求使用两个互不重叠的记录器,求最多可以记录多少个区间。解决方案采用贪心算法,通过排序和遍历实现最优解。 ...
[详细]
蜡笔小新 2024-12-27 18:14:31
-
本文详细介绍C++中实现KMP算法的方法,探讨其在字符串匹配问题上的优势。通过对比暴力匹配(BF)算法,展示KMP算法如何利用前缀表优化匹配过程,显著提升效率。 ...
[详细]
蜡笔小新 2024-12-27 14:45:30
-
探讨一个显示数字的故障计算器,它支持两种操作:将当前数字乘以2或减去1。本文将详细介绍如何用最少的操作次数将初始值X转换为目标值Y。 ...
[详细]
蜡笔小新 2024-12-27 14:34:44
-
本文详细介绍了Java编程语言中的核心概念和常见面试问题,包括集合类、数据结构、线程处理、Java虚拟机(JVM)、HTTP协议以及Git操作等方面的内容。通过深入分析每个主题,帮助读者更好地理解Java的关键特性和最佳实践。 ...
[详细]
蜡笔小新 2024-12-27 13:55:14
-
本文探讨如何设计一个安全的加密和验证算法,确保生成的密码具有高随机性和低重复率,并提供相应的验证机制。 ...
[详细]
蜡笔小新 2024-12-27 13:49:45
-
本文详细介绍了机器学习中广泛应用的决策树算法,通过天气数据集的实例演示了ID3和CART算法的手动推导过程。文章长度约2000字,建议阅读时间5分钟。 ...
[详细]
蜡笔小新 2024-12-27 13:44:59
-
在金融和会计领域,准确无误地填写票据和结算凭证至关重要。这些文件不仅是支付结算和现金收付的重要依据,还直接关系到交易的安全性和准确性。本文介绍了一种使用C语言实现小写金额转换为大写金额的方法,确保数据的标准化和规范化。 ...
[详细]
蜡笔小新 2024-12-27 12:39:06
-
开发笔记:Mongodb副本集集群搭建 ...
[详细]
蜡笔小新 2024-11-30 16:16:20
-
|