和第三章介绍的模乘法一样,根据使用的模运算的不同,模指数在具体实现时也分成利用经典模运算实现的模指数运算、利用Barrett模运算实现的模指数运算、利用Montgomery模运算实现的模指数运算。
首先看看利用经典模运算实现的模指数运算。
───────────────────────────────────────
int BN_mod_exp_simple(BIGNUM *r, const BIGNUM *a, const BIGNUM *p, const BIGNUM *m)
功能: 大数的模指数运算(利用经典模运算实现)
输入: a【基数】,p【指数】,m【模数】
输出: r ← 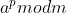
返回: 1【正常】 or 0【出错】 or -1【p为CONSTTIME属性】
出处: bn_exp.c
───────────────────────────────────────
再来看看利用Barrett约化实现的模指数运算。
───────────────────────────────────────
int BN_mod_exp_recp(BIGNUM *r, const BIGNUM *a, const BIGNUM *p,const BIGNUM *m)
功能: 大数的模指数运算(利用Barrett约化实现)
输入: a【基数】,p【指数】,m【模数】
输出: r ← 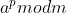
返回: 1【正常】,0【出错】
出处: bn_exp.c
───────────────────────────────────────
接着来看看利用Montgomery约化实现的模指数运算。注意此时需要模数为奇数,否则不满足Montgomery约化的基本条件gcd(m,R)=1。
───────────────────────────────────────
int BN_mod_exp_mont(BIGNUM *rr, const BIGNUM *a, const BIGNUM *p,const BIGNUM *m, BN_MONT_CTX *in_mont)
功能: 大数的模指数运算(利用Montgomery约化实现)
输入: a【基数】,p【指数】,m【模数】,in_mont【Montgomery模数】
输出: r ← 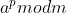
返回: 1【正常】,0【出错】
出处: bn_exp.c
───────────────────────────────────────
当基数a退化成一个字的时候,利用Montgomery约化实现的模指数运算变成:
───────────────────────────────────────
int BN_mod_exp_mont_word(BIGNUM *rr, BN_ULONG a, const BIGNUM *p,const BIGNUM *m, BN_MONT_CTX *in_mont)
功能: 字的模指数运算(利用Montgomery约化实现)
输入: a【字】,p【指数】,m【模数】,in_mont【Montgomery模数】
输出: r= 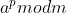
返回: 1【正常】 or 0【出错】 or -1【p为CONSTTIME属性】
出处: bn_exp.c
───────────────────────────────────────
在做模指数运算时使用Barrett约化和Montgomery约化比使用经典模运算好,进一步,使用Montgomery约化的模指数运算应该是最优的[7],但是必需满足条件gcd(m,R)=1。
下面将要介绍的这个模指数运算综合运用了上面提到的BN_mod_exp_recp(利用Barrett约化实现)和BN_mod_exp_mont(利用Montgomery约化实现)。因为使用Montgomery约化的模指数运算是最优的,所以当模数m为奇数时,调用Montgomery约化实现的模指数运算BN_mod_exp_mont。当m为偶数的时候,不满足Montgomery约化的基本条件gcd(m,R)=1,无法使用Montgomery约化,所以改为调用利用Barrett约化实现的模指BN_mod_exp_recp。
───────────────────────────────────────
int BN_mod_exp(BIGNUM *r, const BIGNUM *a, const BIGNUM *p, const BIGNUM *m)
功能: 大数的模指数运算
输入: a【基数】,p【指数】,m【模数】
输出: r ← 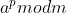
返回: 1【正常】 or 0【出错】
出处: bn_exp.c
备注: 当m为偶数时,利用Barrett约化,当m为奇数时,利用Montgomery约化实现。
───────────────────────────────────────