在说明前,我也是查了大量文档,弄清楚各个名词的意思,才写下这篇博客。。。
特征值和特征向量:
根据公式: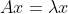
A是n*n的方阵(必须是方阵),x是特征向量,λ是特征值。
一般情况下,会有n个特征值,和n个特征向量。(这里的一般是指方阵是满秩,各行各列都是线性无关)。
引出问题:如果不是n*n维的矩阵,怎么求?
假设矩阵X是m*n,则可以求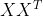 或
或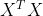 矩阵的特征分解。
矩阵的特征分解。
一般的非方阵的特征分解称为奇异值分解。
奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,奇异值分解则是特征分解在任意矩阵上的推广。在信号处理、统计学等领域有重要应用。
奇异值分解SVD:
A是m*n大小的矩阵
根据公式: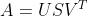
U是左奇异矩阵
同理V是右奇异矩阵
剩下一个S:奇异值矩阵,理论上S的大小应该是m*n才能满足矩阵乘法运算。
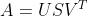 =》
=》 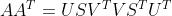 =》
=》 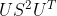
理解: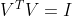 , V是单位正交基,不知道的可百度。
, V是单位正交基,不知道的可百度。
理解: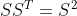 ,S是奇异值,一般的是n行一列的矩阵,为了方便计算,我们设计S变成对角矩阵,即n*1 =》n*n。
,S是奇异值,一般的是n行一列的矩阵,为了方便计算,我们设计S变成对角矩阵,即n*1 =》n*n。
右奇异矩阵举例:
其中V是矩阵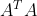 的特征向量, n*n大小
的特征向量, n*n大小
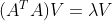 得到奇异值
得到奇异值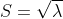 ,且S是n列矩阵,V是n*n维,反求左奇异值
,且S是n列矩阵,V是n*n维,反求左奇异值
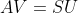 =》
=》 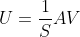 最后得到U是m*n维
最后得到U是m*n维
即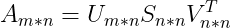
左奇异矩阵举例:
其中U是矩阵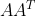 的特征向量 m*m大小
的特征向量 m*m大小
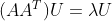 得到奇异值
得到奇异值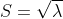 ,且S是m列矩阵,U是m*m维,反求右奇异值
,且S是m列矩阵,U是m*m维,反求右奇异值
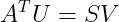 =》
=》 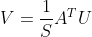 得到V是n*m维(这里是U的转置)
得到V是n*m维(这里是U的转置)
即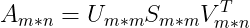
opencv求SVD:
#include
#include using namespace cv;
using namespace std;
void main()
{Mat src &#61; imread("1.jpg", IMREAD_GRAYSCALE);Mat src_ &#61; src.clone();src.convertTo(src, CV_64FC1);Mat U, W, V;SVD::compute(src, W, U, V);int set_dim &#61; min(src.rows, src.cols);//cout <<"W >> <" <" <> <" <" <> <" <" <> " <(i, i) &#61; W.at(i, 0);}Mat dst &#61; U * W_ * V;system("pause");
}
opencv里的W,U,V分别对应前文的 S,U,V^T 且维数计算是左奇异矩阵举例的模式。
利用eigen自己实现svd&#xff1a;
详细看注释
void main()
{Mat m &#61; imread("1.jpg", IMREAD_GRAYSCALE);Mat src &#61; m.clone();Mat S, U;m.convertTo(m, CV_64FC1);double t1 &#61; getTickCount();eigen(m * m.t(), S, U); //求出奇异值矩阵 和 左奇异矩阵U &#61; U.t(); //根据公式 U变成转置后的int set_dim &#61; min(src.rows, src.cols);for (int i &#61; 0; i (i, 0);double sq_val &#61; sqrt(val);S.at(i, 0) &#61; sq_val; //λ &#61; sqrt(S)}Mat V;V &#61; m.t() * U; //根据公式for (int i &#61; 0; i (j, i) &#61; V.at(j, i) / S.at(i, 0);}}Mat Vt &#61; V.t();Mat S_ &#61; Mat(S.rows, S.rows, CV_64FC1, Scalar(0));for (int i &#61; 0; i (i, i) &#61; S.at(i, 0);}dst &#61; U * S_ * Vt;imshow("src", src);imshow("dst", dst);waitKey();}
降维分析&#xff1a;
一直S是对角矩阵&#xff0c;且按降序排列&#xff0c;根据实际测试前10%甚至1%的奇异值就能涵盖99%以上的特征。
可以设置r &#61; ratio * n (ratio&#xff1a;比率)
公式&#xff1a;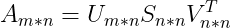 &#xff08;公式1&#xff09;&#61;》
&#xff08;公式1&#xff09;&#61;》 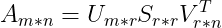 &#xff08;公式2&#xff09;
&#xff08;公式2&#xff09;
如果取r &#61; 0.01&#xff0c;降维后公式2维度是公式1 的 亿分之一。
#include
#include using namespace cv;
using namespace std;Mat getForeMatrix(int rows, int cols, Mat & img, int type)
{Mat tmp &#61; Mat(rows, cols, type, Scalar(0));for (int i &#61; 0; i (i, j) &#61; img.at(i, j);else if (type &#61;&#61; CV_32FC1)tmp.at(i, j) &#61; img.at(i, j);elsetmp.at(i, j) &#61; img.at(i, j);}}return tmp;
}
void main()
{Mat src &#61; imread(filename, IMREAD_GRAYSCALE);Mat src_ &#61; src.clone();src.convertTo(src, CV_64FC1);Mat U, W, V;SVD::compute(src, W, U, V, SVD::Flags::MODIFY_A);double t2 &#61; (getTickCount() - t1) / getTickFrequency();cout <<"cost time >> " <> <" <" <> <" <" <> <" <" <> " <(i, i) &#61; W.at(i, 0);}Mat U_ &#61; getForeMatrix(set_dim, set_rows , U, CV_64FC1);Mat V_ &#61; getForeMatrix(set_rows , V.cols, V, CV_64FC1);Mat dst &#61; U_ * W_ * V_;system("pause")
}
不正确的希望指出。。。不胜感激
更新错误日志2019.12.23&#xff0c;看了下左奇异矩阵举例&#xff1a;不需要将U转置。且更改了一些定义问题
最后&#xff1a;若要显示最终图像&#xff0c;需要将CV_64FC1图像转成CV_8UC1格式。