作者:手机用户2502928341 | 来源:互联网 | 2024-10-19 10:49
本文实例为大家分享了OpenCV实现轮廓外接多边形的具体代码,供大家参考,具体内容如下
取轮廓最大外接矩形
Rect boundingRect( InputArray array );
array:输入的灰度图像或者2D点集,数据类型为vector或者Mat。
该函数可以求取包含输入图像中物体轮廓或者2D点集的最大外接矩形,函数只有一个参数,可以是灰度图像或者2D点集,灰度图像的参数类型为Mat,2D点集的参数类型为vector或者Mat。该函数的返回值是一个Rect类型的变量,该变量可以直接用rectangle()函数绘制矩形。返回值共有四个参数,前两个参数是最大外接矩形左上角第一个像素的坐标,后两个参数分别表示最大外接矩形的宽和高。
轮廓最小外接矩形
RotatedRect minAreaRect( InputArray points );
points:输入的2D点集合
该函数可以根据输入的2D点集合计算最小的外接矩形,函数的返回值是RotatedRect类型的变量,含有矩形的中心位置、矩形的宽和高和矩形旋转的角度。RotatedRect类具有两个重要的方法和属性,可以输出矩形的四个顶点和中心坐标。输出四个顶点坐标的方法是points(),假设RotatedRect类的变量为rrect,可以通过rrect.points(points)命令进行读取,其中坐标存放的变量是Point2f类型的数组。输出矩形中心坐标的属性是center,假设RotatedRect类的变量为rrect,可以通过opt=rrect.center命令进行读取,其中坐标存放的变量是Point2f类型的变量。
外接多边形
void approxPolyDP( InputArray curve,
OutputArray approxCurve,
double epsilon, bool closed );
- curve:输入轮廓像素点。
- approxCurve:多边形逼近结果,以多边形顶点坐标的形式给出。
- epsilon:逼近的精度,即原始曲线和逼近曲线之间的最大距离。
- closed:逼近曲线是否为封闭曲线的标志, true表示曲线封闭,即最后一个顶点与第一个顶点相连。
该函数根据输入的轮廓得到最佳的逼近多边形。
函数的第一个参数是输入的轮廓2D像素点,数据类型是vector或者Mat。
第二个参数是多边形的逼近结果,以多边形顶点坐标的形式输出,是CV_32SC2类型的N×1的Mat类矩阵,可以通过输出结果的顶点数目初步判断轮廓的几何形状。
第三个参数是多边形逼近时的精度,即原始曲线和逼近曲线之间的最大距离。
第四个参数是逼近曲线是否为封闭曲线的标志, true表示曲线封闭,即最后一个顶点与第一个顶点相连。
简单示例
//
// Created by smallflyfly on 2021/6/22.
//
#include "opencv2/opencv.hpp"
#include
using namespace std;
using namespace cv;
int main() {
Mat im = imread("rice.jfif");
// resize(im, im, Size(0, 0), 0.5, 0.5);
Mat gray;
cvtColor(im, gray, CV_BGR2GRAY);
Mat imBin;
threshold(gray, imBin, 150, 255, THRESH_BINARY);
vector> contours;
findContours(imBin, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
Mat im1 = im.clone();
Mat im2 = im.clone();
for (auto & contour : contours) {
// 最大外接矩阵
Rect rect = boundingRect(contour);
rectangle(im, rect, Scalar(0, 0, 255), 1);
// 最小外接矩形
RotatedRect rotatedRect = minAreaRect(contour);
Point2f pts[4];
rotatedRect.points(pts);
Point2f pt = rotatedRect.center;
for (int i = 0; i <4; ++i) {
if (i == 3) {
line(im1, pts[i], pts[0], Scalar(255, 255, 0), 1);
} else {
line(im1, pts[i], pts[i+1], Scalar(255, 255, 0), 1);
}
}
circle(im1, pt, 1, Scalar(0, 0, 255), -1);
// 外接多边形
Mat ploys;
approxPolyDP(contour, ploys, 5, true);
// draw ploy
Vec2i pt1, pt2;
for (int i = 0; i (i);
pt2 = ploys.at(0);
} else {
pt1 = ploys.at(i);
pt2 = ploys.at(i+1);
}
line(im2, pt1, pt2, Scalar(0, 0, 255), 2);
}
}
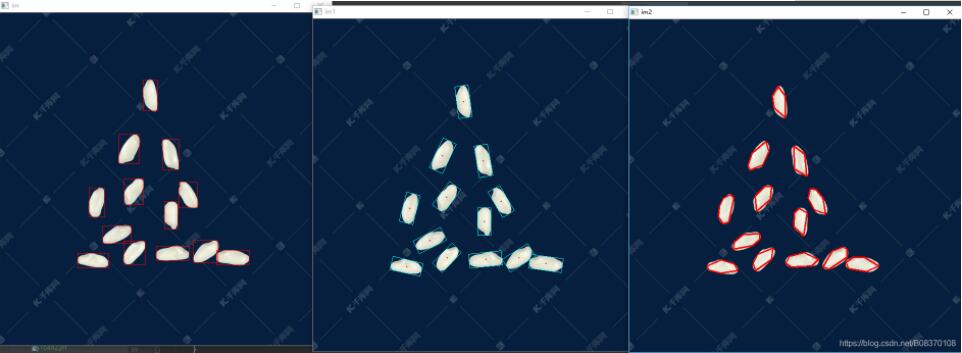
imshow("im", im);
imshow("im1", im1);
imshow("im2", im2);
waitKey(0);
destroyAllWindows();
return 0;
}
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持编程笔记。